聚类之性能度量详解

概念简述

聚类是什么呢？我们都听说过“物以类聚”，即把“志同道合”的 数据分到一起归为一类，不同类之间在”志向“上具有较大分歧。举个栗子，茫茫人生中，我们普通大众会被God根据缘分进行聚类，缘分好的话，会成为朋友，甚至成为了可以互诉衷肠，”余生请指教“的男女盘友，那缘分不好的应该是一生从未谋面或者一面之缘或者是如《再见前任3》中那样成为了最熟悉的陌生人…好像扯远了。
言归正传，用标准的普通话来说，聚类是将数据集中的样本划分为若干个通常是不相交的子集，每个子集成为一个“簇”，用正规的外星人语言来说，对于样本$D= \left \{x _{1},x_{2},...,x_{m}\right \}$包含$m$个无标记样本，每个样本$x_{i}=\left \{ x_{i1};x_{i2};...;x_{in}\right \}$是一个$n$维特征向量，则聚类算法将样本集$D$划分为$k$个不相交的簇$\left \{ C_{l}| l=1,2,...,k \right \}$，其中$C_{l^{'}}\cap _{l^{'}\neq l}C_{l}=\varnothing$且$D=\cup _{l=1}^{k}C_{l}$，相应地，用$\lambda _{j}\in \left \{ 1,2,...,k \right \}$表示样本$x_{j}$的“簇标记”，即$x_{j}\in C_{\lambda_{j}}$。于是聚类的结果可用包含m个元素的簇标记，记向量$\lambda = \left ( \lambda _{1};\lambda _{2};...;\lambda _{m} \right )$。举个栗子，对于具有$10$个样本的数据集$D$，其中每个样本$x_{i}$含有$2$维特征，分成$2$类的结果如下：

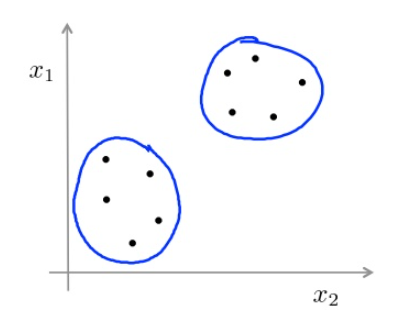
聚类通常用来对无标记训练样本的学习来揭示数据内在性质及规律，为进一步的数据分析提供基础，是“无监督学习”中应用最广的研究方法。那么问题来了，如何衡量聚类结果的好坏呢？按照什么样的“缘分”分类呢？官方的话来说聚类有哪些性能度量以及距离计算方法。

性能度量

我们通常按照一个标准来分析聚类之后的结果，简单来说这个标准是“簇内相似度高，簇间相似度低”，下面我们用一堆“指数”，“系数”来数学化引号里面的内容，权当填补那些好奇心强盛的孩纸们…

性能度量分类：

聚类性能度量的主要分为两类，一类是将聚类结果与某个“参考模型”进行比较，成为“外部指标”；另一类是直接考察聚类结果而不用任何参考模型，成为“内部指标”。

1. 外部指标

“外部指标”通常有Jaccard系数(Jaccard Coefficient，简称JC)、FM系数(Fowlkes and Mallows Index，简称FMI)、Rand指数(Rand Index，简称RI)。

• JC:
  $$\mathrm{JC}=\frac{a}{a+b+c} \tag{1.1}$$
• FMI:
  $$\mathrm{FMI}=\sqrt{\frac{a}{a+b}\cdot \frac{a}{a+c}} \tag{1.2}$$
• RI
  $$\textrm{RI}=\frac{2(a+d))}{m(m-1)} \tag{1.3}$$
  假设，数据集$D= \left \{x _{1},x_{2},...,x_{m}\right \}$，经过聚类后得到的簇划分为$C=\left \{ C_{1},C_{2},...,C_{s}\right \}$，参考模型给出的簇划分$C^{\ast }=\left \{ C_{1}^{\ast},C_{2}^{\ast},...,C_{s}^{\ast}\right \}$，相应的，令$\lambda$和$\lambda^{\ast}$分别表示与$C$和$C^{\ast}$对应的簇标记向量，于是$a、b、c、d$定义如下：
  $$a=\left | SS \right |,SS=\left \{(x_{i},x_{j})|\lambda _{i}=\lambda _{j},\lambda _{i}^{\ast}=\lambda _{j}^{\ast},i< j\right \} \tag{1.4}$$
  $$b=\left | SD \right |,SD=\left \{(x_{i},x_{j})|\lambda _{i}=\lambda _{j},\lambda _{i}^{\ast}\neq \lambda _{j}^{\ast},i< j\right \}\tag{1.5}$$
  $$c=\left | DS \right |,DS=\left \{(x_{i},x_{j})|\lambda _{i}\neq\lambda _{j},\lambda _{i}^{\ast}= \lambda _{j}^{\ast},i< j\right \}\tag{1.6}$$
  $$d=\left | DD \right |,DD=\left \{(x_{i},x_{j})|\lambda _{i}\neq\lambda _{j},\lambda _{i}^{\ast}\neq \lambda _{j}^{\ast},i< j\right \}\tag{1.7}$$
  从上述表达式可知，集合$SS$包含了在$C$中隶属于相同簇且在$C^{\ast}$中也隶属于相同簇的样本对，集合$SD$包含了在$C$中隶属于相同簇但在$C^{\ast}$中隶属于不同簇的样本，集合$DS$包含了在$C$中隶属于不同簇但在$C^{\ast}$中隶属于相同簇的样本，集合$DD$包含了在$C$中隶属于不同簇且在$C^{\ast}$中隶属不同簇的样本，由于每个样本对$\left ( x_{i} ,x_{j}\right )(i<j)$仅能出现在一个集合中，因此有$a+b+c+d=m(m-1)/2$成立。显然，上述性能度量的结果值均在$\left [ 0,1 \right ]$区间，值越大越好。
  2.内部指标
  常用的内部指标有DB指数(Davies-Bouldin Index，简称DBI)和Dunn指数(Dunn Index，简称DI)。
  
  • DB:
    $$\mathrm{DBI}=\frac{1}{k}\sum_{i=1}^{k}max_{j\neq i}\left ( \frac{avg\left ( C_{i} \right ) +avg\left ( C_{j} \right )}{d_{cen}\left (\mu _{i} ,\mu _{j}\right )}\right )\tag{2.1}$$
  • DI:
    $$\mathrm{DI}=min_{1\leq i\leq k}\left \{ min_{j\neq i}\left ( \frac{d_{min}\left ( C_{i} ,C_{j}\right )}{max_{1\leq l\leq k}diam\left ( C_{l} \right )} \right ) \right \}\tag{2.2}$$
    其中：
    $$avg\left ( C \right )=\frac{2}{\left | C \right |\left ( \left | C \right |-1 \right )}\sum _{1\leq i< j\leq \left | C \right |}dist\left ( x_{i},x_{j} \right )\tag{2.3}$$
    $$diam\left ( C \right )=max_{x_{1}\leq i< j\leq \left | C \right |}dist\left ( x_{i},x_{j} \right )\tag{2.4}$$
    $$d_{min}\left ( C_{i},C_{j}\right )=min_{x_{i}\in C_{i},x_{j}\in C_{j}}dist\left ( x_{i},x_{j} \right )\tag{2.5}$$
    $$d_{cen}\left ( C_{i},C_{j} \right)=dist\left ( \mu _{i} ,\mu _{j}\right )\tag{2.6}$$
    注意：$dist\left ( \cdot,\cdot\right )$用于计算两个样本之间的距离；$\mu$代表簇$C$的中心点$\mu =\frac{1}{\left | C \right |}\sum _{1\leq i\leq \left | C \right |}x_{i}$，$avg(C)$对应于簇$C$内样本间的平均距离，$diam(C)$对应于簇内最远距离，$d_{min}(C_{i},C_{j})$代表簇$C_{i}$与簇$C_{j}$内最近样本间的距离，$d_{cen}\left ( C_{i},C_{j} \right )$代表簇$C_{i}$与簇$C_{j}$中心点的距离。显然$\mathrm{DBI}$的值越小越好，而$\mathrm{DI}$则相反，值越大越好。

---

更多机器学习干货、最新论文解读、AI资讯热点等欢迎关注”AI学院(FAICULTY)”
欢迎加入faiculty机器学习交流qq群：451429116 点此进群
版权声明：可以任意转载，转载时请务必标明文章原始出处和作者信息.

---

参考文献

[1]. 周志华，机器学习，清华大学出版社，2016