机器学习强基计划5-2：用一个例子通俗理解贝叶斯网络(附例题)

0 写在前面

机器学习强基计划聚焦深度和广度，加深对机器学习模型的理解与应用。“深”在详细推导算法模型背后的数学原理；“广”在分析多个机器学习模型：决策树、支持向量机、贝叶斯与马尔科夫决策、强化学习等。强基计划实现从理论到实践的全面覆盖，由本人亲自从底层编写、测试与文章配套的各个经典算法，不依赖于现有库，可以大大加深对算法的理解。

🚀详情：机器学习强基计划(附几十种经典模型源码)

---

本文主要通过案例宏观上介绍引入贝叶斯网络的动机及其概念，关于贝叶斯网络的微观结构、概率影响是如何通过网络流动的、有向分离、推断算法等概念，请看

• 机器学习强基计划5-3：图文详解因子分解与独立图I-Map(附例题分析+Python实验)
• 机器学习强基计划5-4：图文详解影响流动性与有向分离(D-分离)(附Python实现)
• 机器学习强基计划5-5：用一个例子通俗理解变量消除法VE原理(附Python实验)

1 从一个案例出发

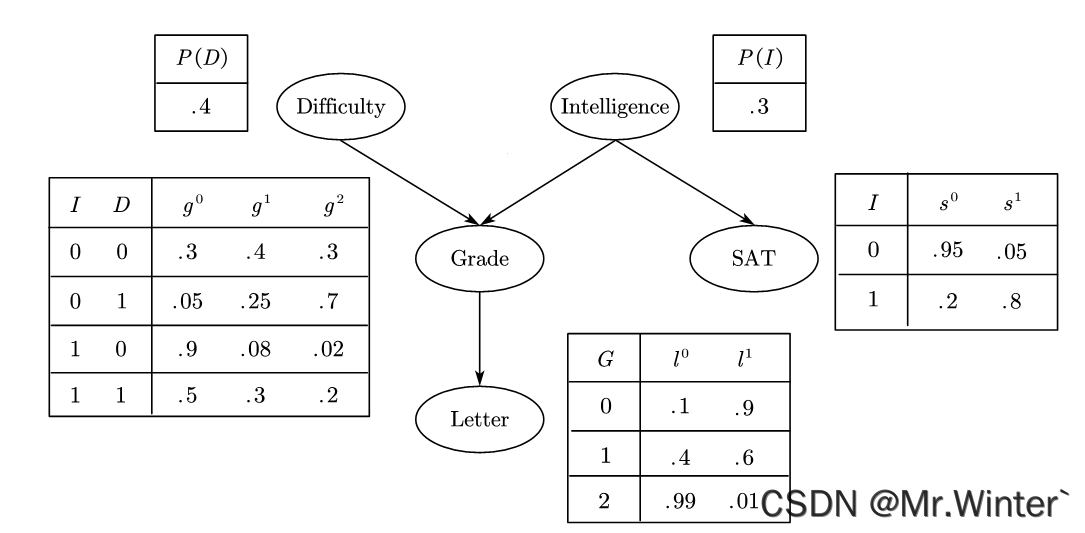
例1：学生成绩$G$不仅取决于他的智商$I$，同时也取决于课程的难度$D$。学生请求教授为其写推荐信，教授仅能通过查看该生的成绩单来决定推荐信的好坏$L$。学生的智商一定程度上也影响了其高考成绩$S$。通过一种最直观的因果关系组织本例的5个随机变量如图所示，其中除成绩可以取“优”、“良”、“中”三个值外，其他均为二值随机变量。

现在就这个案例提几个问题：

1. 分析该生能获得好的推荐信的概率；
2. 分析该生有高智商的概率；
3. 课程成绩$G$已知时，课程难度$D$会影响推荐信$L$的好坏吗？
4. 课程难度$D$已知时，推荐信质量$L$会影响成绩$G$高低吗？
5. 智商$I$已知时，课程成绩$G$会影响高考成绩$S$吗？
6. 课程成绩$G$已知时，课程难度$D$会影响智商$I$吗？

围绕这几个问题逐步引出贝叶斯网络的定义。

2 概率推断

2.1 因果推断

对于问题1，在对该生其他信息一无所知的前提下，获得好的推荐信的概率

$$P\left(l^1\right)=\sum _{g}P\left(l^1|g\right)P\left(g\right)=\sum _{g}P\left(l^1|g\right)\sum _{i,d}P\left(g|i,d\right)P\left(i\right)P\left(d\right)\approx 50.2\%$$

如果得知该生智商不高，那么可能成绩$G$不太好，从而影响其推荐信的质量

$$P\left(l^1|i^0\right)=\sum _{g}P\left(l^1|g\right)P\left(g|i^0\right)=\sum _{g}P\left(l^1|g\right)\sum _{d}P\left(g|i^0,d\right)P\left(d\right)\approx 38.9\%$$

如果进一步得知课程比较简单，那么成绩$G$可能得到提升，从而影响其推荐信的质量

$$P\left(l^1|i^0,d^0\right)=\sum _{g}P\left(l^1|g\right)P\left(g|i^0,d^0\right)\approx 51.3\%$$

这类从原因顺流而下推断结果的过程称为因果推断或预测。

2.2 证据推断

对于问题2，在对该生其他信息一无所知的前提下，其具有高智商的概率即为先验概率$P\left(i^1\right)=30\%$，假设获知该生成绩$G$不太好，则可以怀疑其不具有高智商

$$P\left(i^1|g^2\right)=\frac{P\left(g^2|i^1\right)P\left(i^1\right)}{P\left(g^2\right)}=\frac{P\left(i^1\right){\sum }_{d}P\left(g^2|i^1,d\right)P\left(d\right)}{{\sum }_{i,d}P\left(g^2|i,d\right)P\left(i\right)P\left(d\right)}\approx 7.89\%$$

这类从结果逆流而上回溯原因的过程称为证据推断或解释。

3 概率独立

3.1 间接因果作用

直观地，若课程成绩$G$未知，则当课程较难时，成绩较差的可能性提升，获得好的推荐信的概率下降；同理当课程较容易时，获得好的推荐信的概率提升。相反，若课程成绩$G$已知，则推荐信的好坏$L$可以直接由$G$推断——课程难度$D$无法改变已观测的事实来影响$L$，换言之，课程难度$D$的影响已被包含在课程成绩$G$的影响中

$$\left(L\perp D|G\right)\Rightarrow P\left(l|g,d\right)=P\left(l|g\right)$$

3.2 间接证据作用

直观地，无论课程难度$D$是否已知，推荐信的好坏$L$都可以作为证据来影响对课程成绩$G$的判断，例如即使已知课程很难，但若该生获得好的推荐信仍可以提高其课程取得高分的概率$P\left(g^0|d^1,l^1\right)>P\left(g^0|d^1\right)$。

3.3 共同的原因

直观地，若智商$I$未知，则当课程成绩$G$较好时，可以作为该生智商$I$较高的证据，从而导致其高考成绩$S$较好的信度上升；同理当课程成绩$G$较差时，其高考成绩$S$较好的信度下降。相反，若智商$I$已知，课程成绩$G$的好坏就不会对高考成绩$S$的判断提供任何额外信息

$$\left(G\perp S|I\right)\Rightarrow P\left(s^1|g^1,i^1\right)=P\left(s^1|i^1\right)$$

3.4 共同的作用

直观地，若课程成绩$G$未知，则课程难度$D$和智商$I$互相独立 ，因为证据$G$不充分，无法回溯影响对原因的判断。相反，若课程成绩$G$已知且假设较差，则当课程较难时，可能以较大的权重解释了成绩较差原因，从而提升该生具有高智商的信度

同理，当课程较容易时，该生具有高智商的信度会急剧下降——低智商成为成绩较差的唯一解释。当某个结果的产生存在多个可能原因时，若其中某些原因很好地解释了结果，则该结果对其他原因的影响会被削弱，称为解释消除(Explaining Away)，例如$P\left(i^1|g^2\right)\approx 7.9\%$但$P\left(i^1|g^2,d^1\right)\approx 11\%$。

4 贝叶斯网络

贝叶斯网络(Bayesian Network)又称信念网络(Belief Network)，模拟了人类推理过程中因果关系的不确定性。贝叶斯网络是一个偶对$\mathcal{B}=\left(\mathcal{G},P\right)$，即由网络拓扑结构以及概率分布两部分组成，其中

• 网络结构$\mathcal{G}=\left(V,E\right)$是有向无环图(Directed Acyclic Graphical, DAG)，$V$是图形中所有节点——随机变量的集合；$E$是所有有向连边——变量间因果依赖的集合，如图所示。
  
  网络结构蕴含一系列独立性断言，其中直观的是因果独立性断言
  I l ( G ) = { ( X i ⊥ N o n D e s c e n d e n c e X i ∣ P a X i ) ∣ ∀ X i ∈ B } \mathcal{I} _l\left( \mathcal{G} \right) =\left\{ \left( X_i\bot \mathrm{NonDescendence}_{X_i}|\mathrm{Pa}_{X_i} \right) |\forall X_i\in \mathcal{B} \right\} Il​(G)={(Xi​⊥NonDescendenceXi​​∣PaXi​​)∣∀Xi​∈B}
  即在给定父节点的条件下，每个节点与其非后代节点条件独立，但后代节点在被观测到的前提下，仍可作为证据影响该节点

• 概率分布$P$是在网络结构$\mathcal{G}$上的因子分解，满足
  $$P\left(X_1,X_2,\cdots ,X_m\right)=\prod _i^{m}P\left(X_i|{\mathrm{P}\mathrm{a}}_{X_i}\right)$$
  上式也称为贝叶斯网络链式法则，单个因子称为网络的局部概率模型。

5 贝叶斯网络例题分析

例2：如图所示的贝叶斯网络，令$P\left(Burglary=False|JhonCalls=True，MaryCalls=True\right)\equiv P\left(\neg B|J,M\right)$，求$P\left(\neg B|J,M\right)$的归一化概率

---

🔥 更多精彩专栏：

• 《ROS从入门到精通》
• 《机器人原理与技术》
• 《机器学习强基计划》
• 《计算机视觉教程》
• …

👇源码获取 · 技术交流 · 抱团学习 · 咨询分享 请联系👇