σ-代数
设 为非空集合,
为非空集合, 中的元素是
中的元素是  的子集合,满足以下条件的集合系
的子集合,满足以下条件的集合系 称为
称为 上的一个σ代数:
上的一个σ代数:
-
 在
在
 中;
中;
-
如果一个集合
 在
在
 中,那么它的
差集
中,那么它的
差集
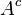 也在
也在
 中;
中;
-
如果有可数个集合
 都在
都在
 中,那么它们的
联集也在
中,那么它们的
联集也在
 中。
中。
用数学语言来表示,就是
不借助逻辑符号的话,也可以使用如下更简洁的定义:设 为非空集合。则
为非空集合。则 上的一个σ代数是指其幂集的子集合
上的一个σ代数是指其幂集的子集合  对有限个差集、交集跟可数个并集这三种运算都依然属于
对有限个差集、交集跟可数个并集这三种运算都依然属于  ,也就是说
,也就是说  对这三运算是封闭(closed)的 。
对这三运算是封闭(closed)的 。
在测度论里  称为一个可测空间。 集合族
称为一个可测空间。 集合族  中的元素,也就是
中的元素,也就是  的某子集,称为可测集合。而在概率论中,这些集合被称为随机事件。
的某子集,称为可测集合。而在概率论中,这些集合被称为随机事件。
例子
- 有两个σ-代数的简单例子,它们分别是:
 上含集合最少的σ代数
上含集合最少的σ代数 ;和
;和 上含集合最多的σ代数是
上含集合最多的σ代数是 的幂集
的幂集 。
。
- 假设集合
 ,那么
,那么 是集合
是集合 上的一个σ代数。这也是所有包含
上的一个σ代数。这也是所有包含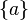 的σ代数中最“小”的一个。
的σ代数中最“小”的一个。
概率空间
概率空间(Ω, F, P)是一个总测度为1的测度空间(即P(Ω)=1).
第一项Ω是一个非空集合,有时称作“样本空间”。Ω 的集合元素称作“样本输出”,可写作ω。
第二项F是样本空间Ω的幂集的一个非空子集。F的集合元素称为事件Σ。事件Σ是样本空间Ω的子集。集合F必须是一个σ-代数:
 ;
;- 若
 ,则
,则 ;
; - 若
 ,
, ,则
,则
(Ω, F)合起来称为可测空间。事件就是样本输出的集合,在此集合上可定义其概率。
第三项P称为概率,或者概率测度。这是一个从集合F到实数域R的函数, 。每个事件都被此函数赋予一个0和1之间的概率值。
。每个事件都被此函数赋予一个0和1之间的概率值。
概率测度经常以黑体表示,例如 或
或 ,也可用符号"Pr"来表示。
,也可用符号"Pr"来表示。
分布函数的性质
对于特定的随机变量  ,其分布函数
,其分布函数 是单调不减及右连续,而且
是单调不减及右连续,而且 ,
, 。这些性质反过来也描述了所有可能成为分布函数的函数:设
。这些性质反过来也描述了所有可能成为分布函数的函数:设 ![F:[-\infty,\infty] \to [0,1], F(-\infty)=0, F(\infty)=1](https://upload.wikimedia.org/math/1/2/8/1283a9612a1acc8eac7e2bfb982414ab.png) 且单调不减、右连续,则存在概率空间
且单调不减、右连续,则存在概率空间 及其上的随机变量 X ,使得 F 是 X 的分布函数,即
及其上的随机变量 X ,使得 F 是 X 的分布函数,即  设
设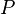 为概率测度,
为概率测度, 为随机变量则函数
为随机变量则函数  (
(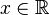 ) 称为
) 称为 的概率分布函数.如果将
的概率分布函数.如果将 看成是数轴上的随机点的坐标,那么,分布函数
看成是数轴上的随机点的坐标,那么,分布函数 在
在 处的函数值就表示
处的函数值就表示 落在区间
落在区间![(-\infty,x]](https://upload.wikimedia.org/math/b/2/7/b27ac59ac8e050f8343b712b19ae8f71.png) 上的概率。
上的概率。
二项分布
概率质量函数
一般地,如果随机变量 服从参数为
服从参数为 和
和 的二项分布,我们记
的二项分布,我们记 或
或 .n次试验中正好得到k次成功的概率由概率质量函数给出:
.n次试验中正好得到k次成功的概率由概率质量函数给出:
对于k = 0, 1, 2, ..., n,其中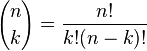
是二项式系数(这就是二项分布的名称的由来),又记为C(n, k),nCk,或nCk。该公式可以用以下方法理解:我们希望有k次成功(pk)和n − k次失败(1 − p)n − k。然而,k次成功可以在n次试验的任何地方出现,而把k次成功分布在n次试验中共有C(n, k)个不同的方法。
在制造二项分布概率的参考表格时,通常表格中只填上n/2个值。这是因为k > n/2时的概率可以从它的补集计算出:
因此,我们要看另外一个k和另外一个p(二项分布一般不是对称的)。然而,它的表现不是任意的。总存在一个整数M,满足
作为k的函数,表达式ƒ(k; n, p)当k < M时单调递增,k > M时单调递减,只有当(n + 1)p是整数时例外。在这时,有两个值使ƒ达到最大:(n + 1)p和(n + 1)p − 1。M是伯努利试验的最可能的结果,称为众数。注意它发生的概率可以很小。
累积分布函数
累积分布函数可以表示为:
其中 是小于或等于x的最大整数。
是小于或等于x的最大整数。
它也可以用正则化不完全贝塔函数来表示:
期望和方差
如果X ~ B(n, p)(也就是说,X是服从二项分布的随机变量),那么X的期望值为
方差为
这个事实很容易证明。首先假设有一个伯努利试验。试验有两个可能的结果:1和0,前者发生的概率为p,后者的概率为1 − p。该试验的期望值等于μ = 1 · p + 0 · (1−p) = p。该试验的方差也可以类似地计算:σ2 = (1−p)2·p + (0−p)2·(1−p) = p(1 − p).
一般的二项分布是n次独立的伯努利试验的和。它的期望值和方差分别等于每次单独试验的期望值和方差的和:
正态分布又叫高斯分布
正态分布的定义
有几种不同的方法用来说明一个随机变量。最直观的方法是概率密度函数,这种方法能够表示随机变量每个取值有多大的可能性。累积分布函数是一种概率上更加清楚的方法,请看下边的例子。还有一些其他的等价方法,例如cumulant、特征函数、动差生成函数以及cumulant-生成函数。这些方法中有一些对于理论工作非常有用,但是不够直观。请参考关于概率分布的讨论。
概率密度函数
正态分布的概率密度函数均值为 方差为
方差为 (或标准差
(或标准差 )是高斯函数的一个实例:
)是高斯函数的一个实例:
-
 。
。
(请看指数函数以及 .)
.)
如果一个随机变量 服从这个分布,我们写作
服从这个分布,我们写作  ~
~  . 如果
. 如果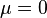 并且
并且 ,这个分布被称为标准正态分布,这个分布能够简化为
,这个分布被称为标准正态分布,这个分布能够简化为
-
 。
。
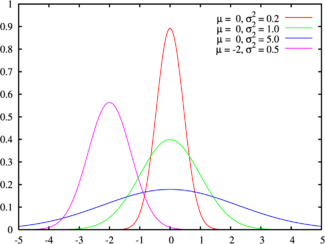
右边是给出了不同参数的正态分布的函数图。
正态分布中一些值得注意的量:
- 密度函数关于平均值对称
- 平均值与它的众数(statistical mode)以及中位数(median)同一数值。
- 函数曲线下68.268949%的面积在平均数左右的一个标准差范围内。
- 95.449974%的面积在平均数左右两个标准差
 的范围内。
的范围内。 - 99.730020%的面积在平均数左右三个标准差
 的范围内。
的范围内。 - 99.993666%的面积在平均数左右四个标准差
 的范围内。
的范围内。 - 函数曲线的反曲点(inflection point)为离平均数一个标准差距离的位置。
累积分布函数
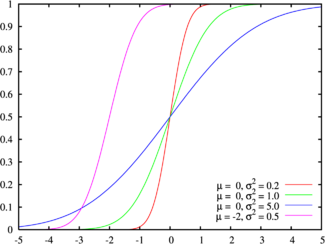
累积分布函数是指随机变数 小于或等于
小于或等于 的概率,用概率密度函数表示为
的概率,用概率密度函数表示为
正态分布的累积分布函数能够由一个叫做误差函数的特殊函数表示:
标准正态分布的累积分布函数习惯上记为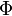 ,它仅仅是指
,它仅仅是指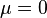 ,
, 时的值,
时的值,
将一般正态分布用误差函数表示的公式简化,可得:
它的反函数被称为反误差函数,为:
该分位数函数有时也被称为probit函数。probit函数已被证明没有初等原函数。
正态分布的分布函数 没有解析表达式,它的值可以通过数值积分、泰勒级数或者渐进序列近似得到。
没有解析表达式,它的值可以通过数值积分、泰勒级数或者渐进序列近似得到。
泊松分布
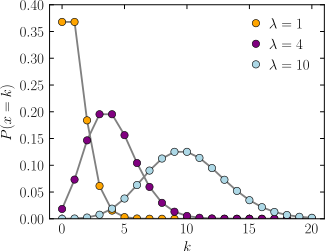 横轴是索引k,发生次数。该函数只定义在k为整数的时候。连接线是只为了指导视觉。
概率质量函数
| |
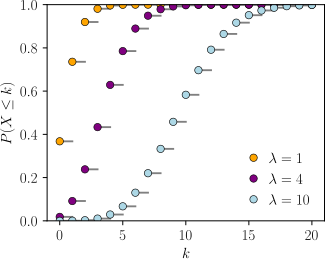 横轴是索引k,发生次数。CDF在整数k处不连续,且在其他任何地方都是水平的,因为服从泊松分布的变量只针对整数值。
累积分布函数
| |
| 参数 | λ > 0(实数) |
|---|---|
| 支撑集 | k ∈ { 0, 1, 2, 3, ... } |
| 概率质量函数 |  |
| 累积分布函数 |
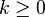 ,其中 ,其中 是不完全Γ函数, 是不完全Γ函数, 是高斯函数,Q是规则化Γ函数) 是高斯函数,Q是规则化Γ函数) |
| 期望值 |  |
| 中位数 | 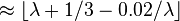 |
| 众数 |  |
| 方差 |  |
| 偏度 |  |
| 峰度 |  |
| 信息熵 |
  |
| 动差生成函数 |  |
| 特性函数 |  |
Poisson分布,译名有泊松分布、普阿松分布、卜瓦松分布、布瓦松分布、布阿松分布、波以松分布、卜氏分配等,又称泊松小数法则(Poisson law of small numbers),是一种统计与概率学里常见到的离散概率分布,由法国数学家西莫恩·德尼·泊松(Siméon-Denis Poisson)在1838年时发表。
泊松分布适合于描述单位时间内随机事件发生的次数的概率分布。如某一服务设施在一定时间内受到的服务请求的次数,电话交换机接到呼叫的次数、汽车站台的候客人数、机器出现的故障数、自然灾害发生的次数、DNA序列的变异数、放射性原子核的衰变数等等。
泊松分布的概率质量函数为:
泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生率。
若 服从参数为
服从参数为 的泊松分布,记为
的泊松分布,记为 ,或记为
,或记为 .
.
性质
1、服从泊松分布的随机变量,其数学期望与方差相等,同为参数λ:E(X)=V(X)=λ
2、两个独立且服从泊松分布的随机变量,其和仍然服从泊松分布。更精确地说,若X ~ Poisson(λ1)且Y ~ Poisson(λ2),则X+Y ~Poisson(λ1+λ2)。
3、其矩母函数为:
泊松分布的来源(泊松小数定律)
在二项分布的伯努利试验中,如果试验次数n很大,二项分布的概率p很小,且乘积λ= np比较适中,则事件出现的次数的概率可以用泊松分布来逼近。事实上,二项分布可以看作泊松分布在离散时间上的对应物。
证明如下。首先,回顾e的定义:
二项分布的定义:
-
 。
。
如果令 ,
,  趋于无穷时
趋于无穷时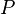 的极限:
的极限:
最大似然估计
给定n个样本值ki,希望得到从中推测出总体的泊松分布参数λ的估计。为计算最大似然估计值,列出对数似然函数:
对函数L取相对于λ的导数并令其等于零:
解得λ从而得到一个驻点(stationary point):
检查函数L的二阶导数,发现对所有的λ与ki大于零的情况二阶导数都为负。因此求得的驻点是对数似然函数L的极大值点:
例子
对某公共汽车站的客流做调查,统计了某天上午10:30到11:47来到候车的乘客情况。假定来到候车的乘客各批(每批可以是1人也可以是多人)是互相独立发生的。观察每20秒区间来到候车的乘客批次,共观察77分钟*3=231次,共得到230个观察记录。其中来到0批、1批、2批、3批、4批及4批以上的观察记录分别是100次、81次、34次、9次、6次。使用极大似真估计(MLE),得到 的估计为200/231=0.8658。
的估计为200/231=0.8658。
生成泊松分布的随机变量一个用来生成随机泊松分布的数字(伪随机数抽样)的简单算法,已经由高德纳给出(见下文参考):
algorithm poisson random number (Knuth):
init:
Let L ← e−λ, k ← 0 and p ← 1.
do:
k ← k + 1.
Generate uniform random number u in [0,1] and let p ← p×u.
while p > L.
return k − 1.
尽管简单,但复杂度是线性的,在返回的值k,平均是λ。还有许多其他算法来克服这一点。有些人由Ahrens和Dieter给出,请参阅下面的参考资料。同样,对于较大的λ值,e-λ可能导致数值稳定性问题。对于较大λ值的一种解决方案是拒绝采样,另一种是采用泊松分布的高斯近似。
对于很小的λ值,逆变换取样简单而且高效,每个样本只需要一个均匀随机数u。直到有超过u的样本,才需要检查累积概率。
algorithm Poisson generator based upon the inversion by sequential search:[1]
init:
Let x ← 0, p ← e−λ, s ← p.
Generate uniform random number u in [0,1].
do:
x ← x + 1.
p ← p * λ / x.
s ← s + p.
while u > s.
return x.















![\operatorname{E}[X] = np](https://upload.wikimedia.org/math/9/e/d/9ed22d6f166c0c97bf4d3df33869a744.png)
![\operatorname{Var}[X] = np(1 - p).](https://upload.wikimedia.org/math/3/b/6/3b66ebdaf066b0f1478a5eddb0932d75.png)


![\Phi(z)=\frac12 \left[1 + \operatorname{erf}\left(\frac{z-\mu}{\sigma\sqrt2}\right)\right] .](https://upload.wikimedia.org/math/8/a/3/8a3995298cb2202cf5b57115a2b256cf.png)

![\Phi(z)=\frac{1}{2} \left[ 1 + \operatorname{erf} \left( \frac{z}{\sqrt{2}} \right) \right].](https://upload.wikimedia.org/math/e/8/a/e8a87f901033e282bb77731fad761171.png)

 ,或
,或 ,或
,或
![\lambda[1 - \log(\lambda)] + e^{-\lambda}\sum_{k=0}^\infty \frac{\lambda^k\log(k!)}{k!}](https://upload.wikimedia.org/math/4/6/b/46bdca4f526c233b1dba425f44b0591b.png) (for large
(for large 
![M_X(t)=E[e^{tX}]=\sum_{x=0}^\infty e^{tX}\frac{e^{-\lambda}\lambda^x}{x!}=e^{-\lambda}\sum_{x=0}^\infty\frac{({e^t}\lambda)^x}{x!}=e^{{\lambda}(e^t-1)}](https://upload.wikimedia.org/math/a/4/0/a40546829ef4788b3ef7aa7e28cd1f13.png)

![\begin{align}\lim_{n\to\infty} P(X=k)&=\lim_{n\to\infty}{n \choose k} p^k (1-p)^{n-k} \\ &=\lim_{n\to\infty}{n! \over (n-k)!k!} \left({\lambda \over n}\right)^k \left(1-{\lambda\over n}\right)^{n-k}\\&=\lim_{n\to\infty}\underbrace{\left[\frac{n!}{n^k\left(n-k\right)!}\right]}_F\left(\frac{\lambda^k}{k!}\right)\underbrace{\left(1-\frac{\lambda}{n}\right)^n}_{\to\exp\left(-\lambda\right)}\underbrace{\left(1-\frac{\lambda}{n}\right)^{-k}}_{\to 1} \\&= \lim_{n\to\infty}\underbrace{\left[ \left(1-\frac{1}{n}\right)\left(1-\frac{2}{n}\right) \ldots \left(1-\frac{k-1}{n}\right) \right]}_{\to 1}\left(\frac{\lambda^k}{k!}\right)\underbrace{\left(1-\frac{\lambda}{n}\right)^n}_{\to\exp\left(-\lambda\right)}\underbrace{\left(1-\frac{\lambda}{n}\right)^{-k}}_{\to 1} \\&= \left(\frac{\lambda^k}{k!}\right)\exp\left(-\lambda\right)\end{align}](https://upload.wikimedia.org/math/0/9/8/098dfaad42d2f1765750172fe9d0ad71.png)


















 7335
7335

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








