《概率论与数理统计》之概率函数、概率分布函数与概率密度函数理解

本文链接：https://blog.csdn.net/FrankieHello/article/details/90741040

文章目录

写在前面

如果有大一大二的新生看到这篇博文，如果你此时正在翘《概率论与数理统计》这门课，无论你以后想打算从事算法岗位，还是做金融量化，或者想走科研的道路，成为大佬，那么就请现在好好学习这门课，因为这也是为了不耽误你们以后撩妹、打游戏的宝贵时间，而又可以系统性学习这门课程的最好时间。

由于最近的研究和学习涉及的理论基础知识越来越多，很多知识点容易混淆，同时也为了可以在今后的论文或者研究中用专业的术语和论证来尽情的表（zhuang）达（bi），因此最近打算重新学一遍《概率论与数理统计（陈希孺编著）》。

当乍一看到概率函数、概率分布函数、概率密度函数以及累积概率函数这一堆术语时，像我这种概率论学习不扎实的必然会头疼，所以打好基础还是很重要的。在学习《概率论》时，引用陈希孺老师的一句话：研究一个随机变量，不只是要看它能取哪些值，更重要的是它取各种值的概率如何，这样就可以把握住核心了，上面这堆术语都是用来描述随机变量的概率的。既然是用来描述随机变量的概率，那下面就先说一下随机变量。

离散型随机变量与连续型随机变量

离散型随机变量（Discrete random variable）与连续型随机变量（Continuous random variable）的区别也很好划分，只要看一下随机变量的取值能否一一列举出来就可以。如掷骰子、扔硬币、性别等，取值都是可以直接列举出来的，这样就是离散型随机变量。而像天气的温度，器件的寿命、测量误差等，这样的取值不能全部列举出来，只能通过一个区间来表示，这样的就是连续型随机变量。

离散型随机变量的概率函数与概率分布函数

离散型随机变量的概率函数也就是用函数的形式来表示随机变量取值的概率。
$X$ 是离散型随机变量，其全部可能取值是 ${a_{1},a_{2},...,a_{n}}$ ，则它的概率函数表示为：
$p_{i} = P(X = a_{i}) \quad (i=1,2,...,n)$
离散型随机变量的概率函数的自变量是离散型随机变量 $X$ 的取值，因变量是对应取值的概率，它给出了将全部概率1在其所有可能值上的分配情况，由于离散型随机变量的有限性，所以也常以列表的形式展示离散型随机变量的概率分布：

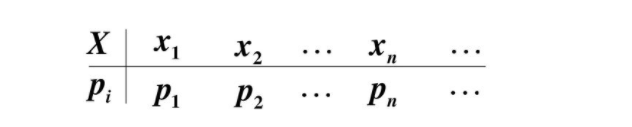
知道了离散型随机变量的概率分布后，那么就来说一下离散型随机变量的概率分布函数，在介绍离散型随机变量的概率分布函数之前，先看一下概率分布函数的定义，注意这里没有区分是离散型还是连续型随机变量：
设 $X$ 为随机变量，则随机变量的概率分布函数为：
$\leq x) = F(x) \quad (- \infty <x< \infty)$
那么，当 $X$ 是离散型随机变量时，它的概率分布函数为：
$\leq x) = \sum_{\{i|a_{i}\leq x\}}p_{i}$
从上面的形式可以看出概率分布函数就是概率函数取值的累加，所以它又叫做累积概率函数（Cumulative Distribution Function）。

连续型随机变量的概率密度函数与概率分布函数

说完了离散型随机变量的概率函数和概率分布函数，下面来说一下连续型随机变量的概率密度函数和概率分布函数。
为什么到了连续型随机变量这里，概率函数就没有了，反而多了一个概率密度函数呢？其实连续型随机变量的概率密度函数就相当于是离散型随机变量的概率函数。试想一下，在离散型随机变量的概率函数表示每个离散值对应的概率的函数，但是连续型随机变量有无穷个数值，单单描述其中一个数值的概率是不可能的，所以就通过了一个区间内的概率密度来表示数据的集中分布程度。
引用陈希孺老师教程中的定义：设连续型随机变量 $X$ 有概率分布函数 $F (x)$ ，则 $F (x)$ 的导数 $f (x) = F^{'} (x)$ 称为 $X$ 的概率密度函数。
可以设想一根极细的无穷长的金属杆，总的质量为1，概率密度相当于各个点的质量密度。
连续型随机变量 $X$ 的密度函数具有以下三条基本性质：
1、 $f(x)\geq0$
2、 $\int_{-\infty}^{\infty}f(x)dx = 1$
3、对于任何常数 $a < b$ ，有 $P(a\leq X \leq b) = F(b) - F(a) = \int_{a}^{b}f(x)dx$
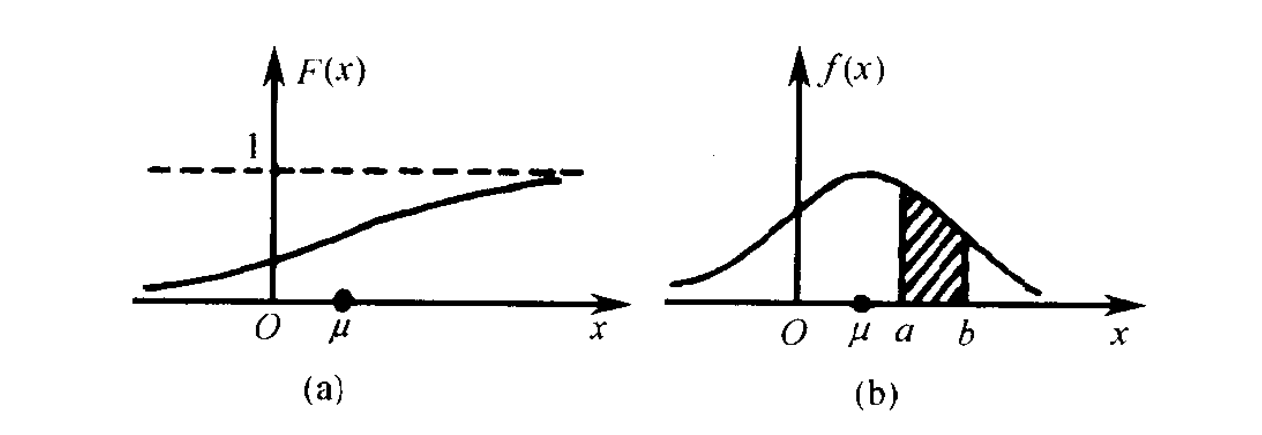
加深一下印象，看一下连续型随机变量最常见的一种分布，正态分布的概率分布函数和概率密度函数：

总结

1、离散型随机变量的概率函数和连续型随机变量的概率密度函数都用来描述随机变量如何在所有取值处分配总的概率1。离散型随机变量的概率函数可以直接得到离散型变量对应的概率值，连续型随机变量则是通过一个区间内概率密度函数的面积来表示概率值。
2、无论是离散型还是连续型概率分布函数，可以按照它的另一个叫法累积概率函数来理解，既然是累积概率，那么得到的公式是一个求和的形式，得到的图像是一个递增的过程。
3、由于概率分布的研究多是侧重于连续型随机变量，毕竟连续型随机变量的概率分布函数和概率密度函数作为连续函数，还有很多可以研究的点，所以后期会再整理一些常见的连续型随机变量的概率分布函数和概率密度函数。