GAMES103（三）Cloth

最新推荐文章于 2024-05-06 13:58:06 发布

ucastfy

最新推荐文章于 2024-05-06 13:58:06 发布

阅读量324

点赞数

分类专栏： games103 文章标签：算法

本文链接：https://blog.csdn.net/Fyantu/article/details/127031031

版权

games103 专栏收录该内容

2 篇文章 0 订阅

订阅专栏

文章目录

一、弹簧系统
二、约束限制

一、弹簧系统

我们知道能量与做功的关系式：
$E_{end} - E_{start} = -W_{start \rightarrow end} = -F \cdot(S_{start} - S_{end})$

因此力是能量的负梯度：

在这里插入图片描述

对有多个受力点的弹簧则可使用加和进行表示：

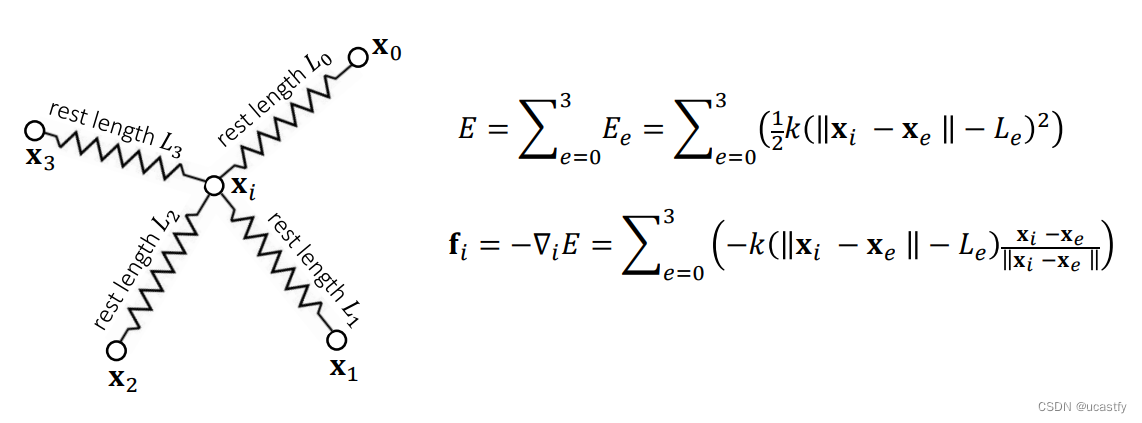
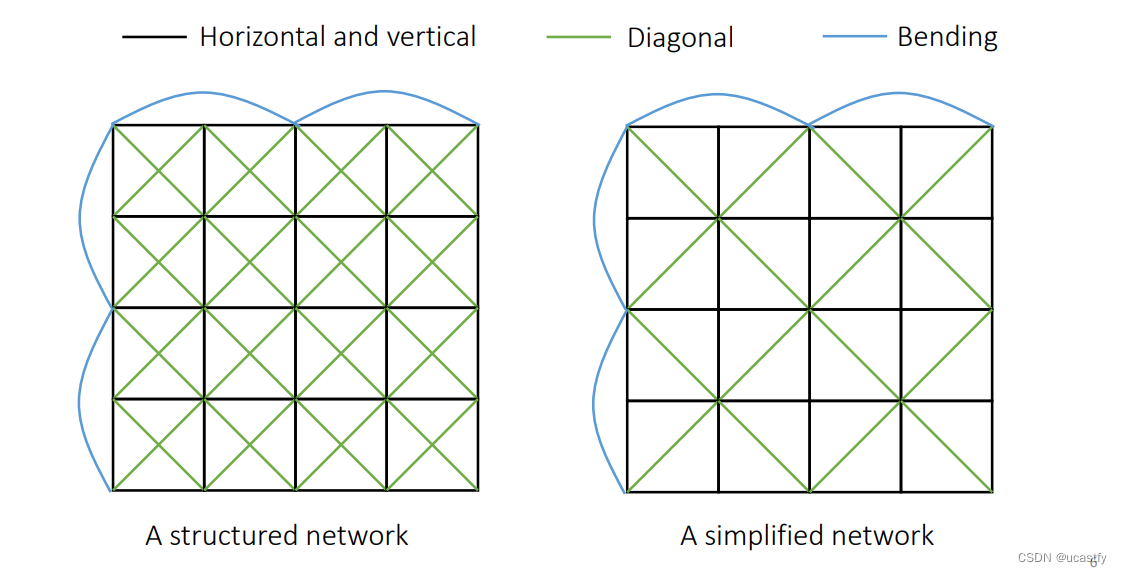
在这里插入图片描述

由此可以形成一个弹簧网格来表示衣服，横竖网格表示衣服的上下左右的移动，斜方格表示 45° 与 135° 的移动，而蓝色的网格则表示衣服可以轴向弯曲的移动。

但一般喜欢选用第二种错开的方式，即一部分 45° 一部分 135° ，这样 45° 和 135° 都可以兼顾，同时也可以让弹簧数量减少。

在这里插入图片描述

对于不规则的面料，一般使用不规则的三角网格表示，使用内部边相对的一个顶点连接来表示弯曲：

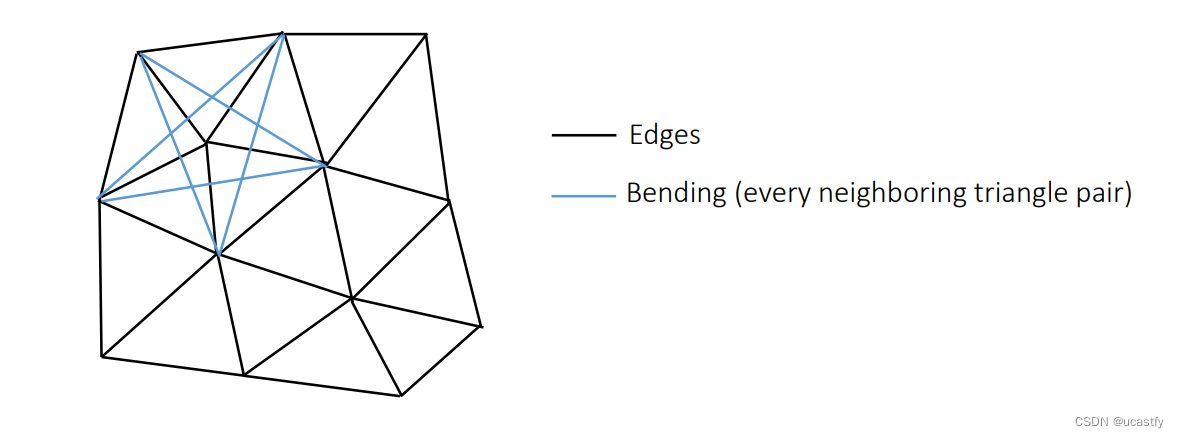
在这里插入图片描述

对网格的表示一般由两种成分组成，一个是顶点的信息，一个是每个三角形的索引。但如果只存储这两种信息，我们寻找网格的内部对边时，每个内部对边可能会被计算两次，因为对边的寻找依赖于内部边，而每个内部边会被两个三角形重复使用。

在这里插入图片描述

因此我们需要设定一种数据结构来寻找内部重复的边，使用一种三元列表的结构来存储边，前两个元素存储顶点索引，第三个元素存储边所在的三角形索引，这样对边结构一排序，重复的边就会相邻，从而可以找出相邻的三角形和不重复的边。

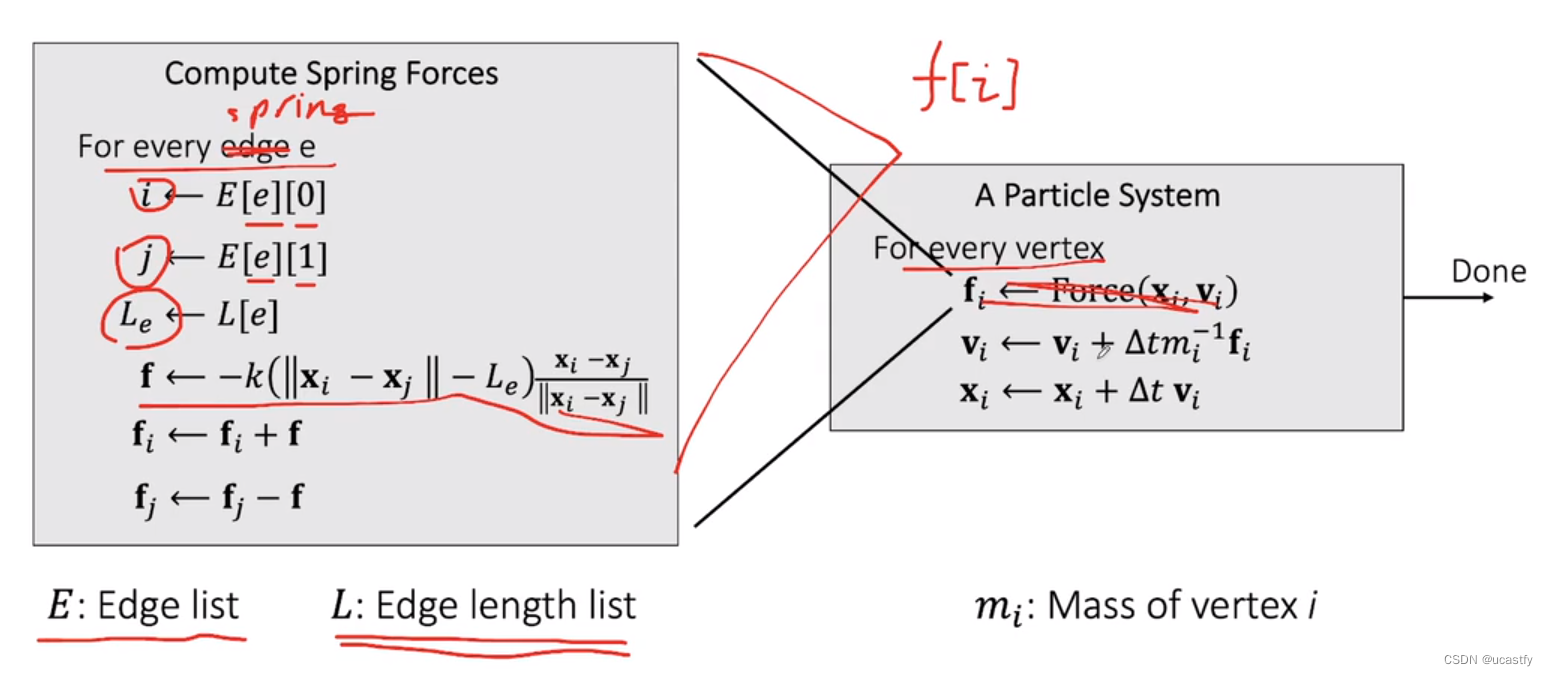
在这里插入图片描述

然后针对网格中的每一条边（也就是弹簧），遍历计算出每一个点的力，得到一个力的数组 $f [i]$ ，再遍历每一条顶点，得到每一个点的合力 $f_i$

在这里插入图片描述

对于弹簧的显式积分，当我们把弹性系数 $k$ 设置的过大时，可能一点位移就会产生很大的力，从而让该点位移很远的距离，以至于移动到了另一侧更远的距离，最后来回震荡以至于弹簧的端点超过了屏幕的范围。

因此使用显式积分容易产生数值不稳定性，他一般在 $k$ 很大 或者 $\Delta t$ 很小 的时候产生，如果将 $\Delta t$ 设置的很小则会影响模拟的效率。

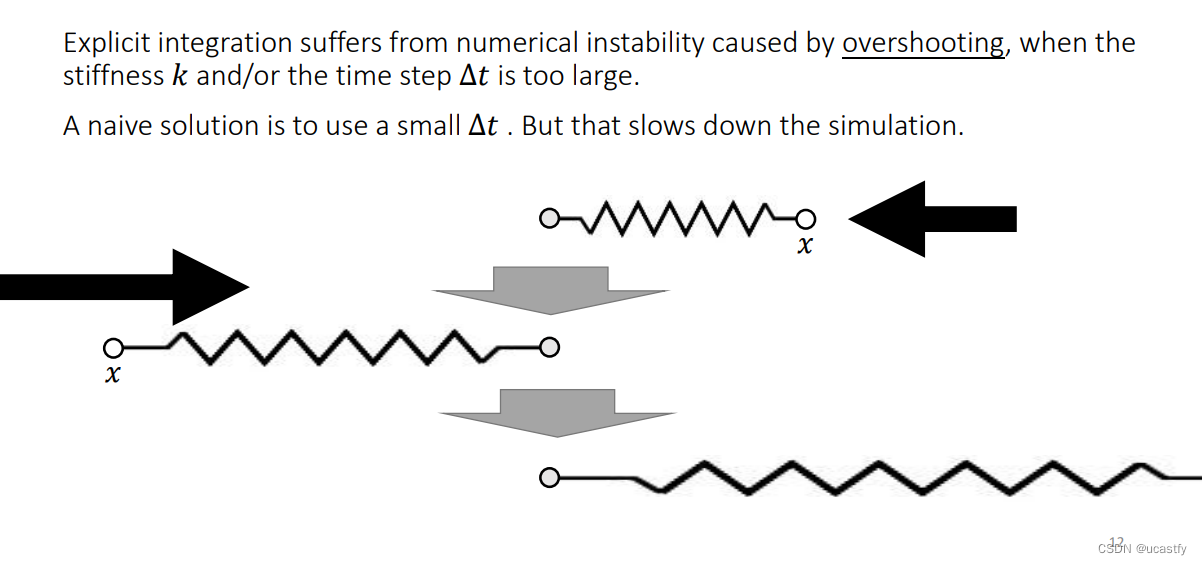
在这里插入图片描述

使用隐式积分法，由于我们对 $[1]$ 时刻的速度和位移是受到 $[1]$ 时刻的力 $f^{[1]}$ 控制的，但我们目前只知道 $[0]$ 时刻的速度和位移，所以得到的式子整体是一个隐式表达。我们需要假设任意时刻的 $f$ 是只和当时的位移 $x$ 有关的，因此两个式子的求解最终变为了对 $x^{[1]}$ 的求解。

在这里插入图片描述

先转换一个视角看待这个方程，把它转换为优化问题，这样可以帮助我们理解模拟中的误差、优化方法、加速方法等，而解线性方程实际上可以理解为只是优化问题中的一个特例。对两边求积分得到 $F (x)$ ，当 $F^{'} (x) = 0$ 时的 $x$ 既为方程组的解，同时又是使 $F (x)$ 为最小值的解。

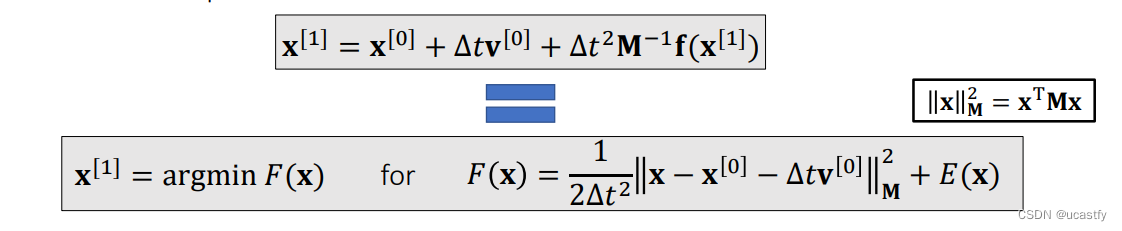
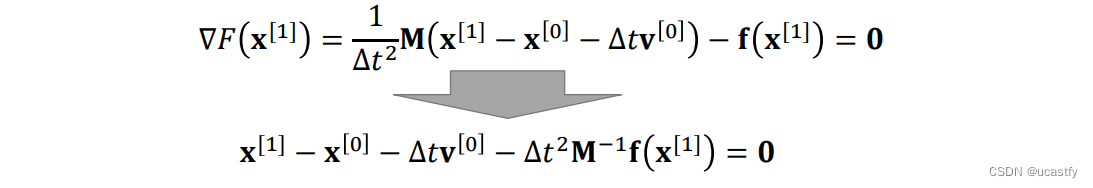
在这里插入图片描述

其中 $M$ 是质量矩阵，每一个对角位置表示对应点的质量：
为什么M是一个3Nx3N矩阵？
$\begin{bmatrix} m_1 & 0 & 0 & ... &0&0&0 \\ 0 & m_2 & 0 & ... &0&0&0\\ ... & ... & ... & ... &0&0&0\\ ... & ... & ... & ... &0&0&0\\ ... & ... & ... & ... &0&m_{n-1}&0\\ ... & ... & ... & ... &0&0&m_n \end{bmatrix} =$
而 $X$ 是一个 $R^{3N}$ 的列向量，存储了之前所有的点信息：
$X^{[1]} = \begin{bmatrix} x_0 \\ x_1 \\ ... \\ x_{n-1}\\ x_n\\ \end{bmatrix}$

由于梯度求导的形式为：
$\nabla f(x) = (\frac{\partial f}{\partial x})^T = \frac{\partial f}{\partial x^T}$
所以
$[\frac{\partial (x^TMx)}{\partial x}]^T = 2M^Tx = 2Mx ~~(M是对角阵)$

1、Newton迭代法

对于隐式方程的求解，我们可以使用牛顿迭代法，当函数具有利普希茨连续性，即函数可以被两条直线夹逼时，牛顿法收敛。

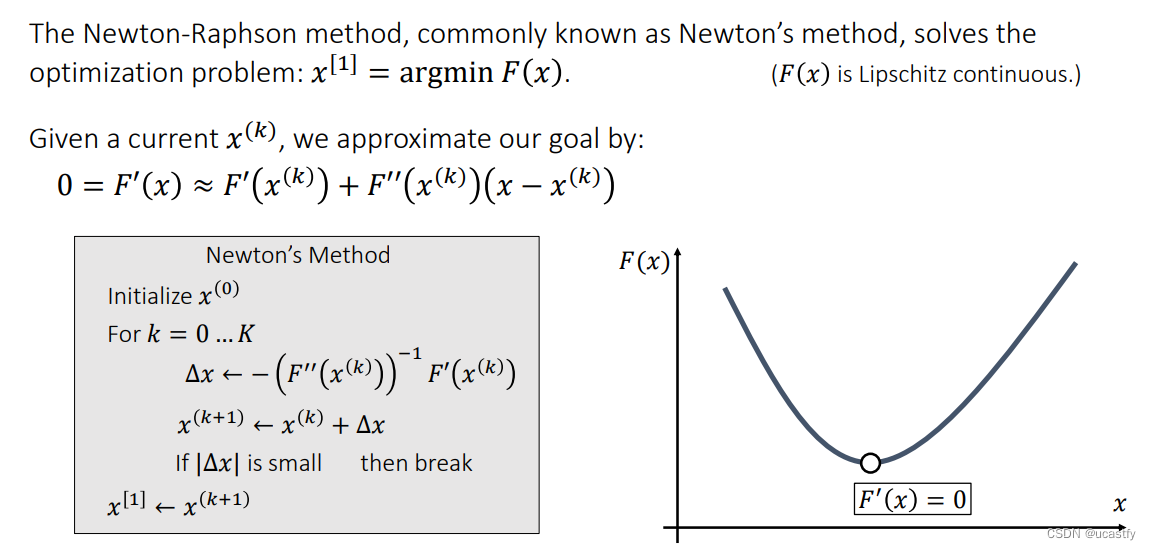
在这里插入图片描述

经过多次迭代后，牛顿法收敛到其中一个解。

在这里插入图片描述

$E$ 则表示了与位置 $x$ 有关的势能， $E$ 的负一阶导数为 $F$ ， $E$ 的二阶导数为可以类比于弹簧的弹性系数。

在这里插入图片描述

因此我们需要求解黄色部分的方程，我们需要判断 $Hess ian$ 矩阵的正定性，这有助判断我们的解是否是唯一的

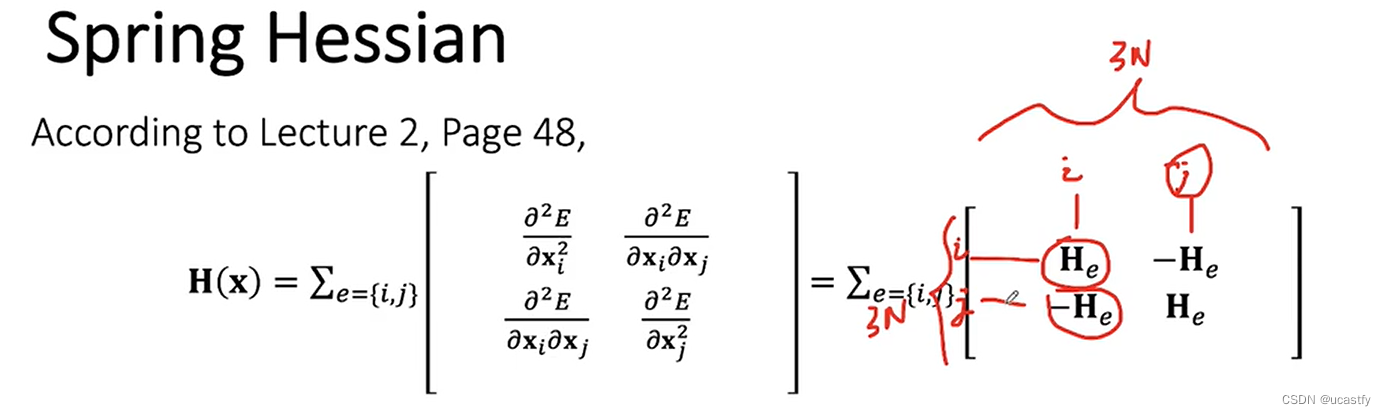
在这里插入图片描述

我么可以看到当弹簧压缩的时候， $H_e$ 可能会不正定，导致最终的 $H (x)$ 不正定，同时导致 $A$ 也可能不正定，矩阵的正定类似于二阶导数，我们知道函数的二阶导数大于0，代表有最小值没有最大值， $Hess ian$ 矩阵同理。

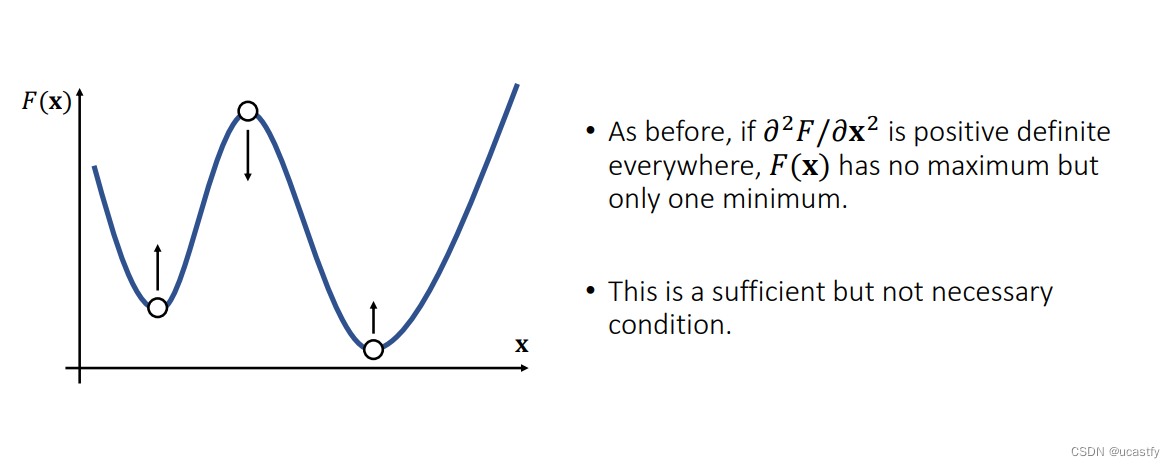
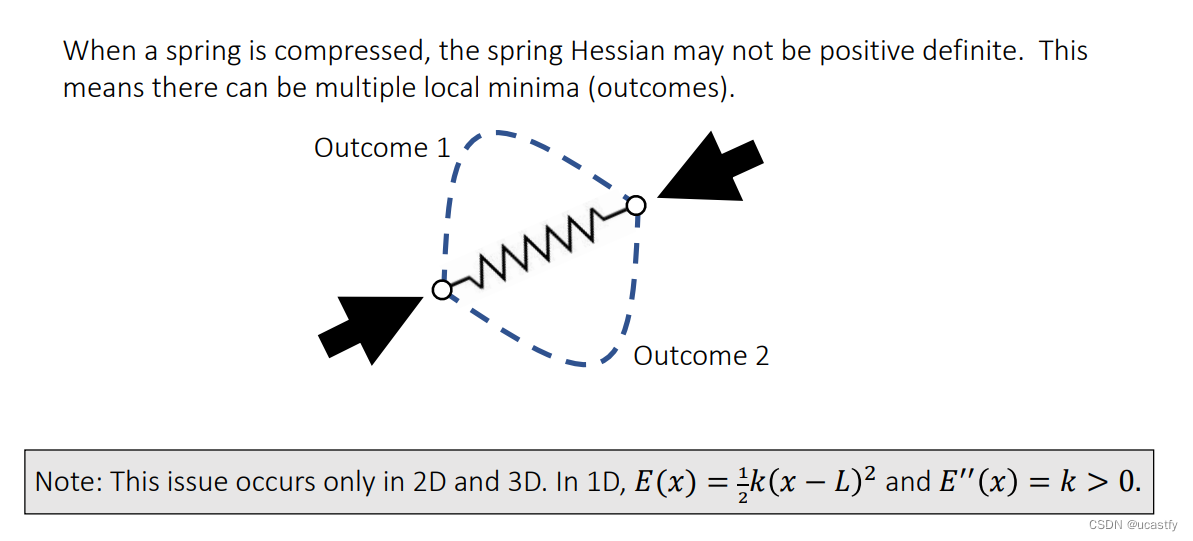
在这里插入图片描述

当 $A$ 正定，我们就有唯一解，但是有唯一解的时候不一定就是正定的。例如 $\Delta t$ 越小越正定，对应的就是我们时间片段越小，意味着每次的变动只动一点，那么模拟起来就越稳定。所以我们也可以推断在拉伸的时候，我们整个系统比较稳定，因为一定是正定的，但压缩的时候就有可能导致 $Hess ian$ 不正定。

对于非正定可能会导致的多个解，在现实生活可以理解为压缩弹簧，弹簧蜷起来的状态一个往上，一个往下。但是这个问题不会出现在一维，因为弹性系数一定大于0.

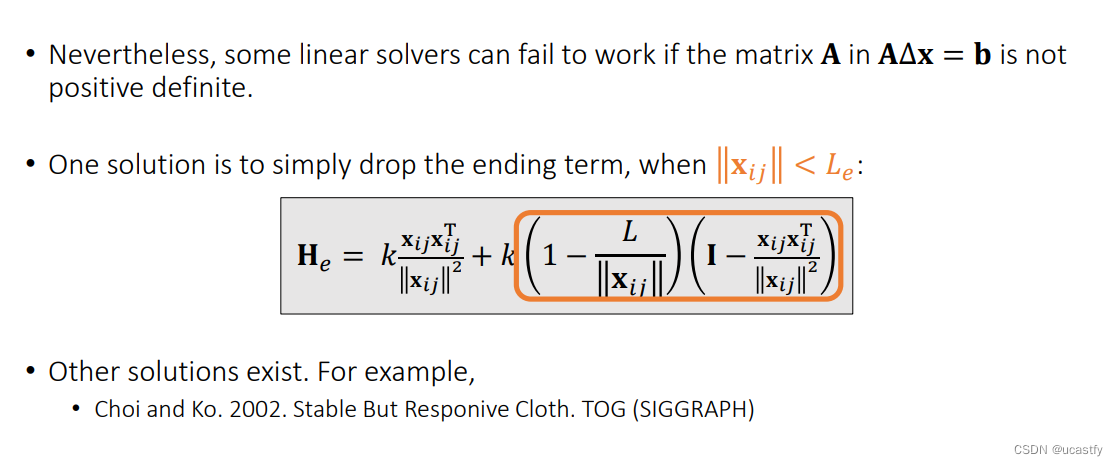
在这里插入图片描述

在实际中，正不正定对于模型的影响还是次要的，主要影响的还是算法上的使用。为了让 $A$ 保持正定，有一种方法是把不正定的部分直接删除。

在这里插入图片描述

Jacobi Method

解线性系统分为直接法和迭代法。

直接法对 A 的要求小，适合在 CPU 上做，有一定内存开销。

迭代法对 A 有一定的要求，例如要求 A 正定，但可以在 GPU 上实现，有一些加速方法。 $J a co bi$ 就是一种迭代法。

使用 $J a co bi$ 方法来解线性方程，前面的 $α$ 一般在对角占优的时候取1。引入 $α$ 来保证解法可以用于更多的情形。

在这里插入图片描述

用切比雪夫法加速 Jacobi 方法的求解速度。

在这里插入图片描述

记录一些课程提问：

$\Rightarrow$ 用能量优化的思路做刚体？

能量优化主要还是用于弹性体、有限元以及衣服模拟，刚体较少。

$\Rightarrow$ 布料模拟的解有解析解对照或者benchmark吗？

弹簧系统的一维作为简谐振动可能有，二维三维可能没有

$\Rightarrow$ 有考虑到弹簧的弯曲吗？

没有考虑，这里的弹簧只考虑了两个点的相对位置，这也导致了弯曲模拟的很多问题

$\Rightarrow$ 隐式积分的泰勒展开线性化和这里的最优化问题是等价的吗？

应该是等价的，等价到里面的线性方程求解

$\Rightarrow$ 质点质量可以不同吗

一般来说是先求一个三角形，将三角形的质量分到三个顶点上去，从而得到每个点不同的质量。

$\Rightarrow$ 迭代法求解支持的维度比直接法更大？

是的，因为直接法有内存开销的问题

$\Rightarrow$ 矩阵直接求逆会不会有无法求解的情况

应该不会，由于 $H (x)$ 是奇异的，前面的 $M$ 大概率也是奇异的，只要矩阵不存在奇异值为0的情况，就是可逆的

2、Bend Model

当弹簧只是产生了一个很微小的弯曲时，它的位移可能只是发生了很小的变化不足以产生对应的抵抗力

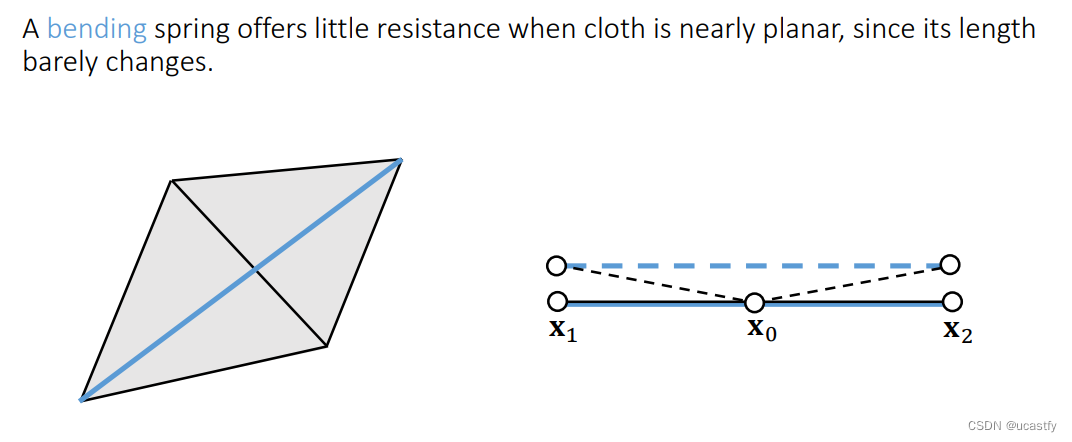
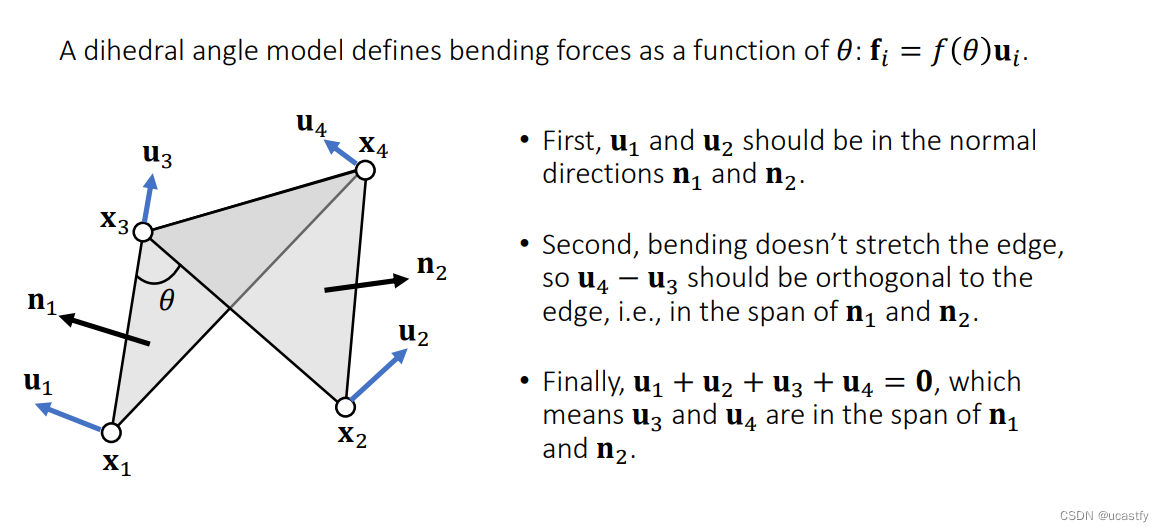
在这里插入图片描述

Dihedral Angle Model

所以将弯曲的角度考虑进来，即通过二面角来表示力，其中 $u_i$ 表示力的方向， $f_i$ 表示力的大小。

使用二面角表示需要满足以下几个定义。其中 $u_4$ 、 $u_3$ 上受到的力应该在 $x_3 →x_4$ 这个方向上为零，所以 $x_3、x_4$ 的线性组合应该都是垂直于 $x_{34}$ 这条边，由于 $n_1、n_2$ 也是垂直于 $x_{34}$ 的，所以 $u_4-u_3$ 应该为 $n_1、n_2$ 的线性组合。

最后一个条件是因为合力要为零。

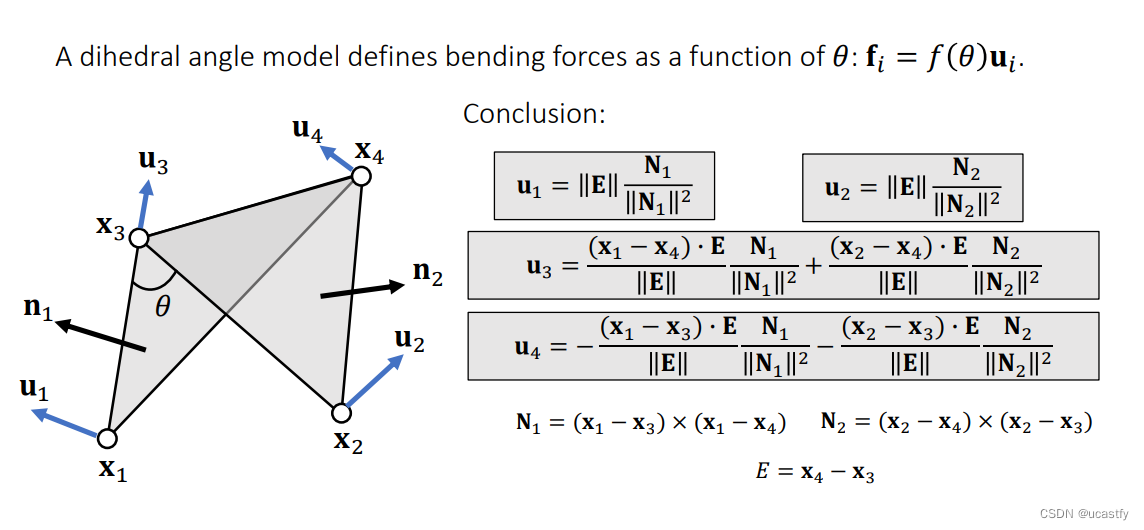
在这里插入图片描述

可以解出 $u_1、u_2、u_3、u_4$ 的值

在这里插入图片描述

其中 $\theta_0$ 为初始的二面角度数， $\theta$ 为弯曲后相对于弯曲前改变的度数，当初始两个面的状态为同一平面时，相当于非平面情况下的 $\theta_0 = 0$ 。

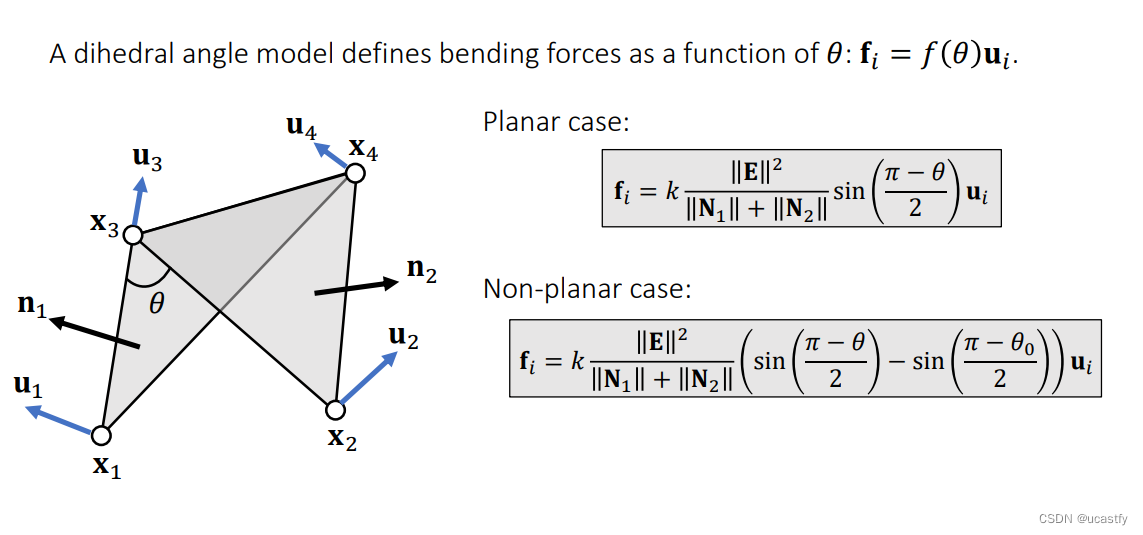
在这里插入图片描述

参考：Simulation of Clothing with Folds and Wrinkles（推荐阅读）

Quadratic Bending Model

使用二面角的方式只考虑到了力，没有考虑到能量，因此只适用于求显式积分，如果使用隐式积分则很难处理。

二次弯曲模型基于两个假设：（1）静止状态下两个三角形形成一个平面（2）顶点间的拉伸比较小，只考虑弯曲

其中 $q^Tx||$ 就是在计算两个三角形的 $L a pl a ce$ ，它代表了两个三角形之间的曲率，当曲率越来越大，能量就会越来越大，其中的 $co t$ 是从 $L a pl a ce$ 算子推三角形的权重推出来的。

在这里插入图片描述

由于 $Q$ 是一个常数矩阵，因此模型的梯度和 $Hess ian$ 比较好算，但针对拉伸很严重的面料模拟就不太准确，如果初始状态不为一个平面也不太合适。

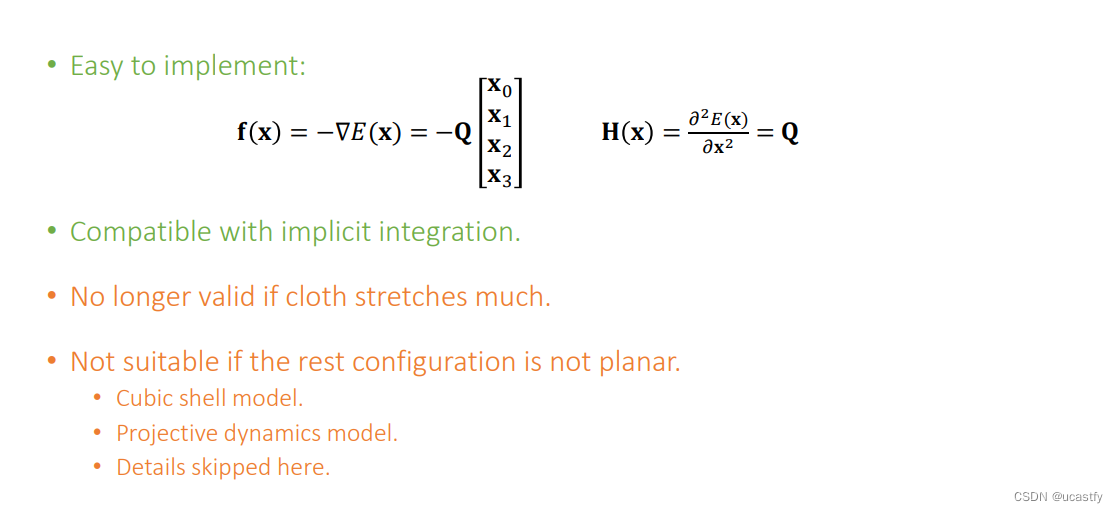
在这里插入图片描述

参考论文：A Quadratic Bending Model for Inextensible Surfaces（推荐阅读）

前面考虑了弹簧在拉伸的情况下各种弯曲的处理，这种考虑的前提是弹簧弯曲和拉伸是独立的，但有的时候也会遇到不能拉伸但可以弯曲的材料比如纸。

但用弹簧模型来模拟不能拉伸的材料时，弹簧的弹性系数非常大，沿着穿着弹簧的边弯曲也会受到很大的阻力，因为弹簧几乎不允许发生形变，也不会跟着弯曲，只要穿过弹簧翻折布料就会受到很大的弹力顶住两端。这被称为 Locking Issue。

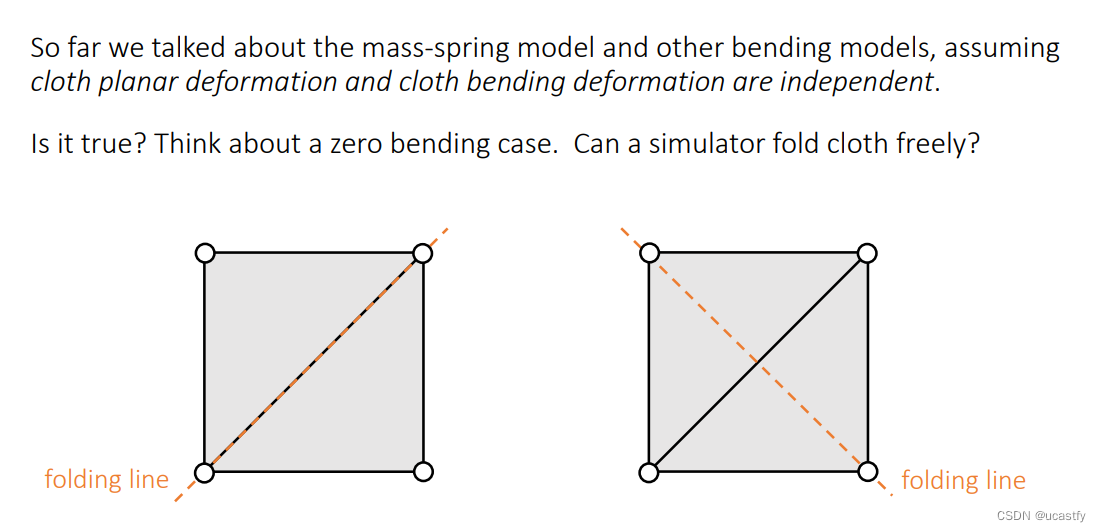
在这里插入图片描述

发生这种的原因是模拟中的自由度不够。

边的数量可以看作是约束的数量，依据欧拉定理：

$E d g es = 3 * v er t i ces - 3 - b o u n d a ry e d g es$
弹簧模型中 Mesh 的顶点可以自由移动，每个顶点有3个自由度（x,y,z)，Mesh 之间的边是约束条件，自由度就等于顶点数*3减边数。
$Do F s = 3 * v er t i ces - E d g es = 3 + b o u n d a ry e d g es$

Locking 问题在弹簧弹性较弱、Mesh 的分辨率低的时候比较明显，那时候模拟就会发现布料弯不下去，因为所有的弹簧都撑在那里

分辨率高可以改善的原因并不是因为加了点导致的自由度高，而是因为顶点相对较密，而改善的，只是增加内部顶点，自由度和约束会同时增加互相抵消。

在这里插入图片描述

解决方法：

压缩的时候把弹性系数减小一点（可以理解为之前由于k太大轴在那，直接把k改小让它可以弯曲）
假定弹簧在一定变化范围内没有力，超过了一定的阈值才开始产生力
把自由度定义在边上（很难实际应用）
参考：Animating Developable Surfaces Using Nonconforming Elements

但以上方法也只能在视觉上减少这个问题，物理本质上还是没有改变。

二、约束限制

在这里插入图片描述

真实世界的布料拉伸到一定程度就会很难再拉伸了，如果只是单纯的增加弹簧系数 $k$ ，显式积分计算会增加很多的不稳定性，隐式积分计算会导致线性系统 $i ll - co n d i t i o n$ ，解决他们的办法都需要进行更大的计算量。

ill-condition：一般指问题的条件数非常大，从而比较难以优化，或者说需要更多迭代次数来达到同样精度

1、spring model

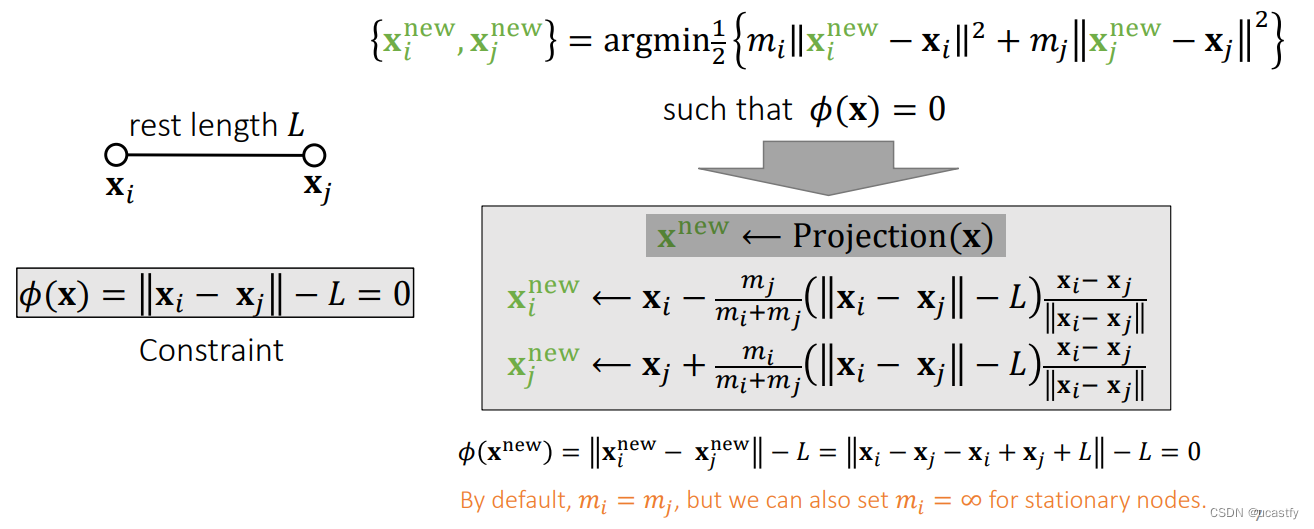
当弹簧的弹性系数无限大时，弹簧的长度成为了一个约束条件。可以定义一个6维的平面，使得平面上的点都满足弹簧长度不变（ $\phi (x)=0$ ），在这种约束下寻找新的点使得弹簧的形变量是最小的。

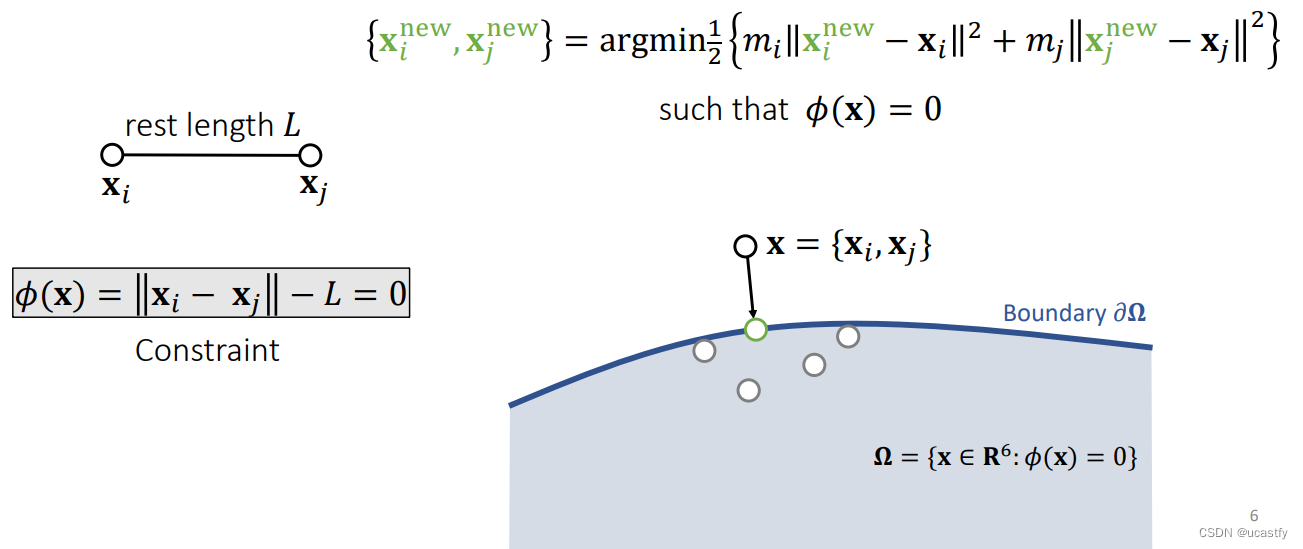
在这里插入图片描述

可以直接算出新的点坐标，直观上理解对于边而言质心是不变的， $x_i$ 、 $x_j$ 则沿着这条边上的方向靠近或远离，而他们移动的距离取决于两个点相对的质量质量大挪的小，质量小挪的大。

新的点的距离仍然保持不变，对于不动点，可以直接让其质量设置为无穷大或者在运行的时候不进行更新。

在这里插入图片描述

Gauss-Seidel Approach

对于多弹簧系统，我们可以对两根弹簧分别更新，不断迭代收敛到最后的两根弹簧的位置。

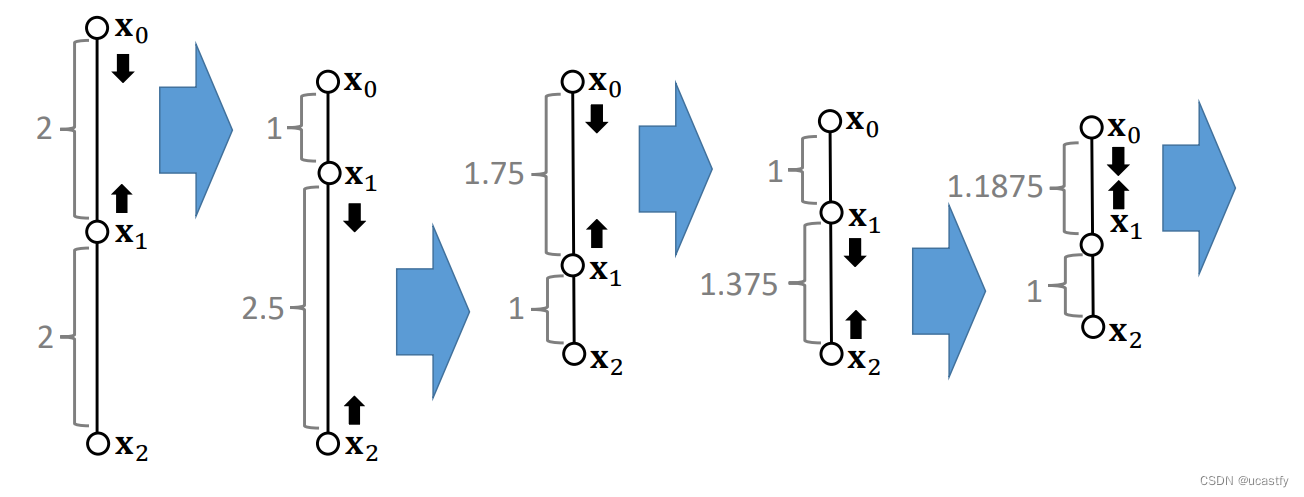
在这里插入图片描述

$G a u ss - S e i d e l$ 类似于深度学习中的随机梯度下降 $(SG D)$ ，迭代次数越多越稳定。对边处理的顺序会影响结果（可能导致最终结果偏向某一边）或者效率（不同顺序所用时间不同）

在这里插入图片描述

Jacobi Approach

为了减小运算顺序对结果的影响，以及为了更好的使用GPU并行计算（Gauss-Seidel也可以并行，但是要复杂一些，可以用一种叫着色法的方法对边进行分类处理)。

$J a co bi$ 方法针对每次对顶点的更新，都先保存下来，等到该顶点的所有更新都保存完毕以后，对得到的所有更新值取一个加权，就可以得到更新的最终结果。

$n_i$ 存储了某个顶点需要更新的数量（因为顶点连着很多条弹簧，每个弹簧都会对同一点更新一次）， $x_i^{new}$ 为每个弹簧对 $x_i$ 的更新，这里的 $α$ 是一个已知的参数，可通过调参来得到最优值。

$J a co bi$ 运行起来很容易，但是迭代次数要多一些。

在这里插入图片描述

2、Position Based Dynamics（PBD)

PBD前半段类似 shape matching 让粒子自由运动，然后通过边长的约束来得到真实的 $x$ 、 $v$

PBD中没有涉及弹性的过程，只约束了边长，它的弹性体现在 迭代次数 和 网格分辨率。迭代数量越多，约束满足越好，就显得越有弹性，网格密度越小，越有弹性。

PBD中更新 $v$ 有加号是因为被相加的 $v$ 是更新过后的，所以要加上原来的速度。

PBD的约束也可以用于体积的约束或者是碰撞约束，关键是需要去定义一个投影函数。
在这里插入图片描述

PBD优点：

非常易于并行，易于实现
通用性强，弹性体甚至流体都可以使用
在不到1000顶点的网格还是可以以实时的效率去进行模拟

PBD缺点：

迭代结果收到网格数量和迭代次数影响，如果使用非常多的网格模拟，反而会导致无法拉伸，产生locking Issue，因此它是没有一个精确解的。所以PBD的方法是没有物理定义的。
在高分辨率的网格下效果下降会非常明显。

解决方法：

Hierarchical approaches：使用一个网格构造低分辨率和高分辨率网格，然后在低分辨率网格上模拟一次，把模拟的结果在放到高分辨率网格上再做一次，再传到更高的分辨率上，层层递进来得到最后的结果。但容易产生抖动问题。

参考： Hierarchical Position Based Dynamics.

迭代加速，例如 $C h e b ys h e v$

PBD方法广泛用于现在的游戏中，由于它每次对内存的访问只有一个更新后的顶点坐标，所以可以提高模型的训练速度，事实上，目前对于矩阵的计算并不是影响计算速度的瓶颈，真实的速度瓶颈还是在内存访问上。

3、Spring Strain Limit

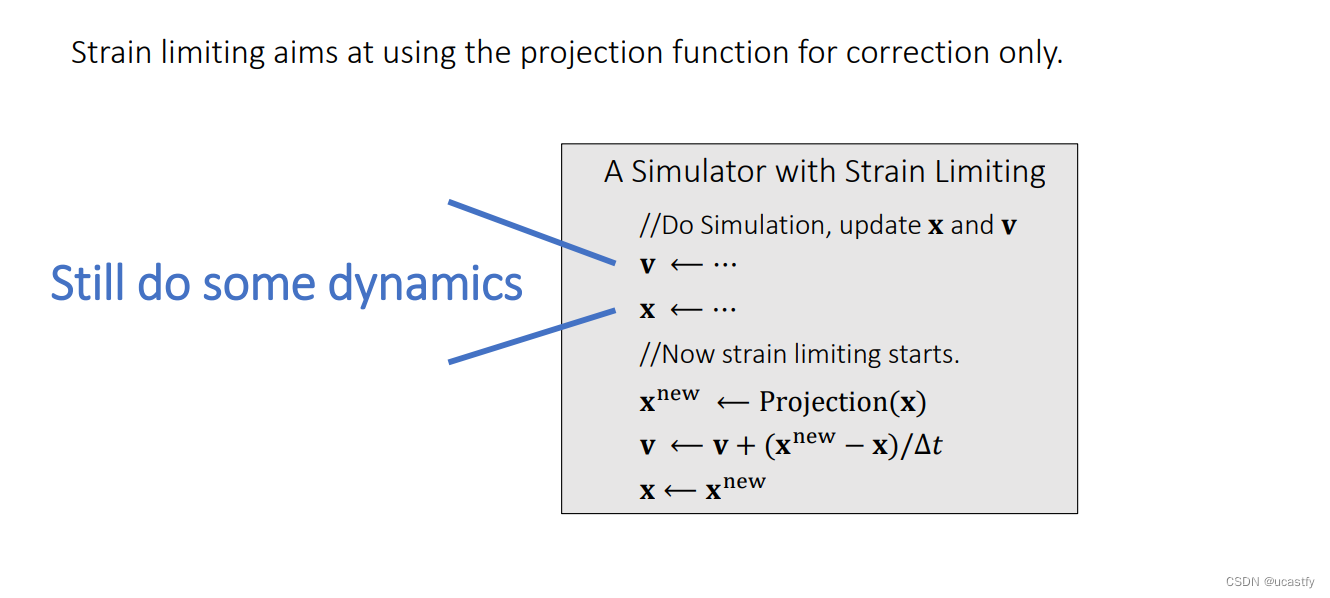
为了减轻投影函数对模型的负担，让模型可以有一些物理含义，因此考虑继续做正常模拟（例如隐式积分、有限元），但是在模拟过程中加入一步防止产生大形变。

在 $Sp r in g St r ain L imi t in g$ 模型中第一步仍然做一些模拟的过程（弹簧、有限元等），而后面的第二步只是做一些约束，让模拟更稳定，而不是完全靠后面的 $St r ain L imi t in g$ 来做模拟。

在这里插入图片描述

首先定义一个弹簧的拉伸比，弹簧的压缩和拉伸都不超过比例范围即可，相比于PBD 的确定长度这个宽松了限制条件。

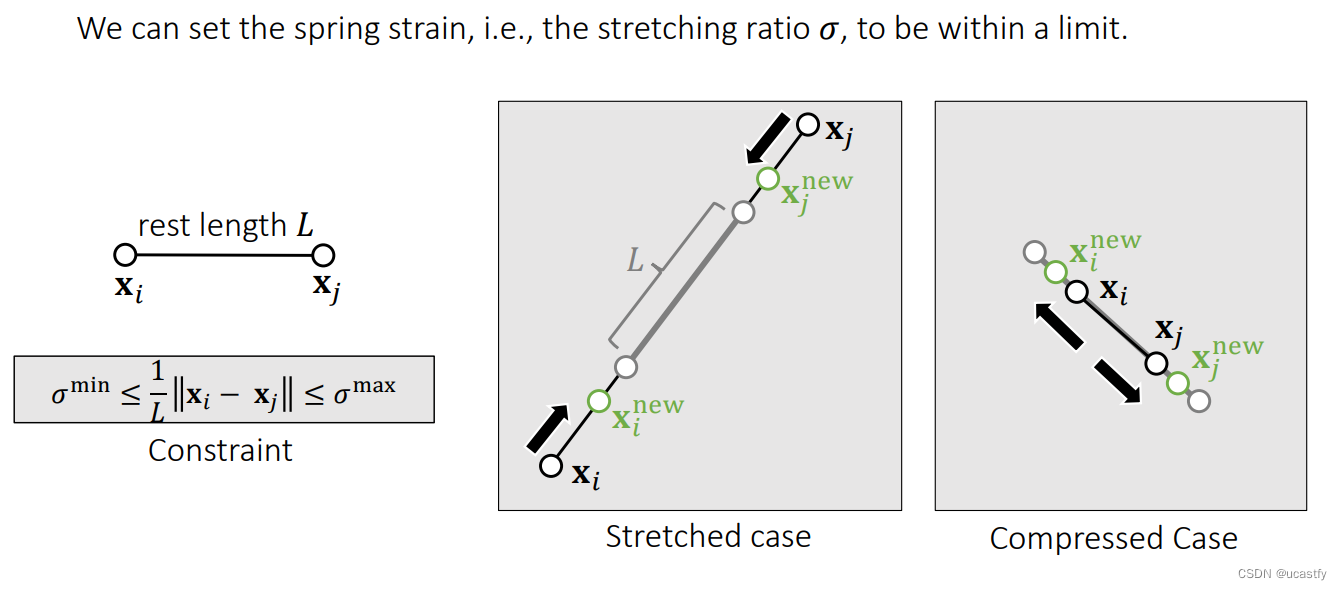
在这里插入图片描述

然后对弹簧进行限制，求出一个约束下的拉伸比，使用拉伸比来更新弹簧两端的位置

在这里插入图片描述

这种方法的本质是为了解决拉伸的问题，但也可以用于解决模拟一些布料拉伸到一定程度很僵硬的情况，或是解决一些弹性体拉伸到很大程度时产生的数值不稳定。

PBD可以看作是该方法的一种特例。

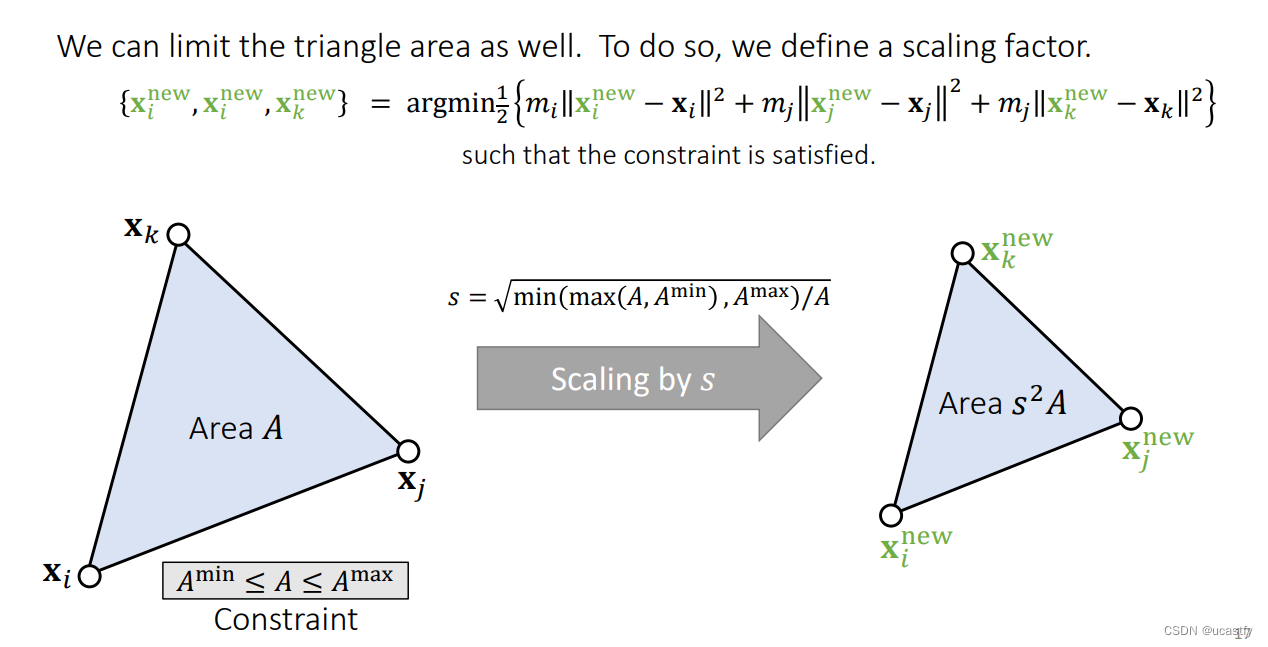
在这里插入图片描述

同理可对三角形的面积进行约束，求出一个面积的缩放比范围，在尽量保持质心不变的情况下，对三角形的三个点进行缩放，三个点缩放的程度依据点与质心的距离。

在这里插入图片描述

这里的 $s$ 要开根号是因为依据面积公式，面积与点与点间的距离是平方关系。保持质心不变从数学上讲是为了满足顶点运动更少的要求，从物理上讲是为了让物体只有本地的运动，没有动量上的变化。

4、Projection Dynamics（PB)

PB 方法与PBD方法最大的不同在于用约束处理不同的东西。PBD是用约束条件直接修改顶点的位置，而PB方法是用约束条件得到新的顶点位置之后，使用定义的能量函数来进行模拟。

新算出的顶点位置 $x_{e,i}^{new}$ 、 $x_{e,j}^{new}$ 应该满足保持弹簧原长（弹性势能最小），并且移动的方向是在原来的 $x_i-x_j$ 方向上。由于 $\frac {x_i-x_j}{||x_i-x_j||}$ 是一个单位向量，依据范数的齐次性可以直接提出去，最后得到的 $E (x)$ 和弹簧能量函数是一样的。

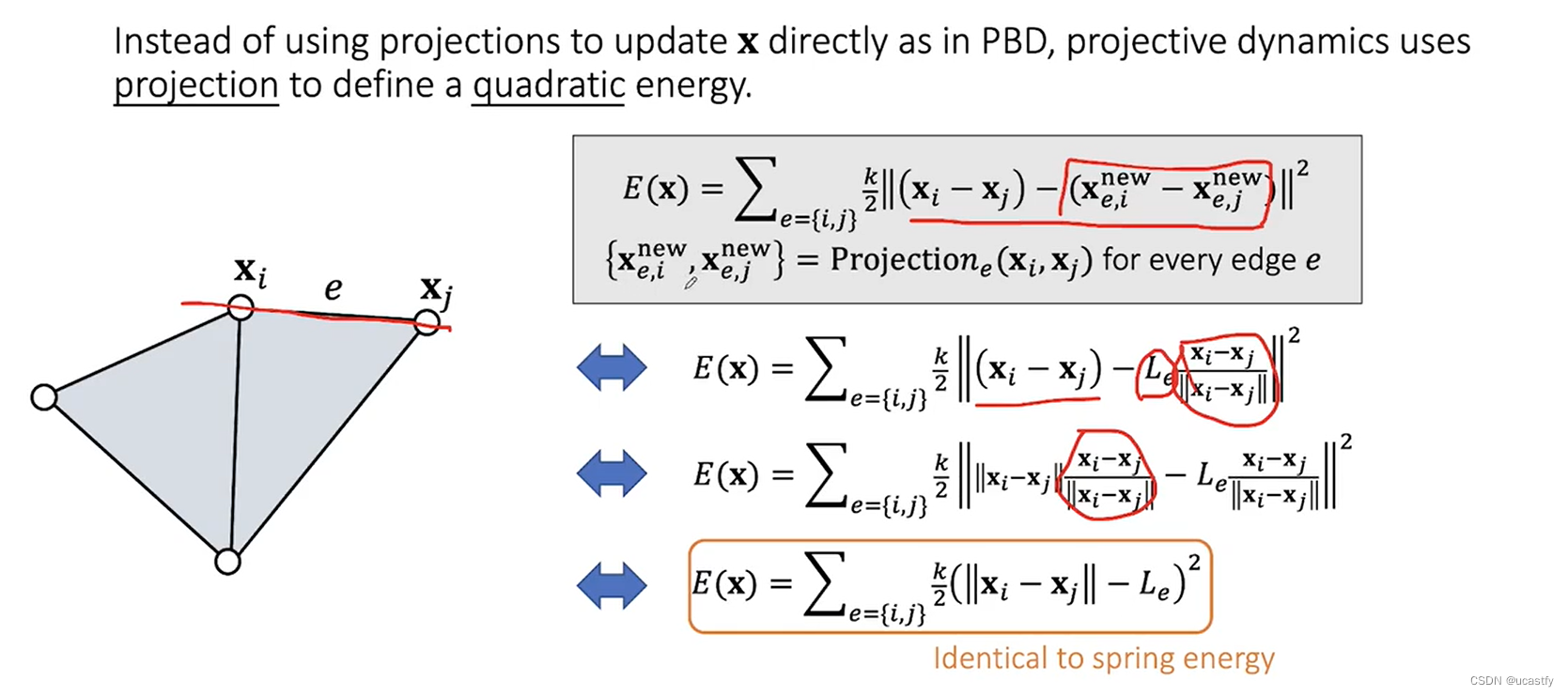
在这里插入图片描述

将能量中的 $x_{e,i}^{new}-x_{e,j}^{new}$ 定义为一个不变量，这样能量函数中只有一个变量 $x_i$ 再求导即可得到 $x_i$ 的力，可以发现该点收到的力和弹性势能和弹簧模型中定义的是一致的。

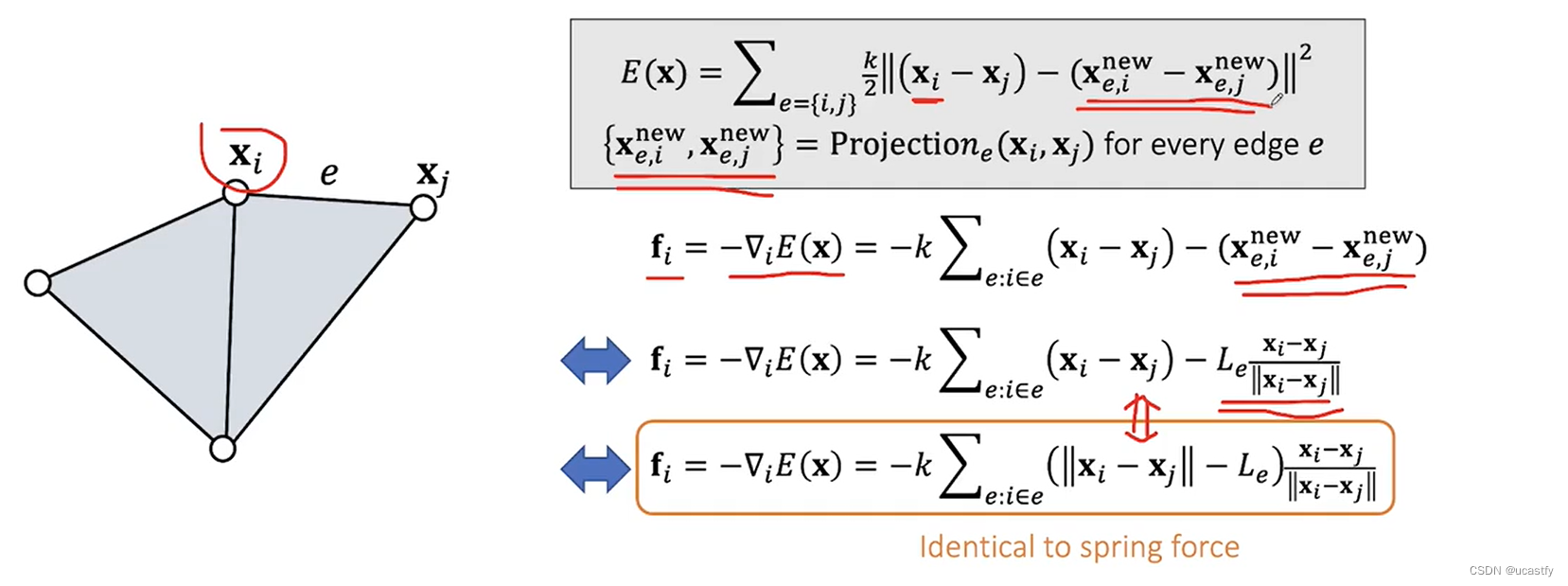
在这里插入图片描述

虽然力和能量与弹簧模型一致，但 $PB$ 方法构造出的 $Hess ian$ 是不一样的，这是 $PB$ 方法的关键。由于我们假定了新的弹簧长度部分是一个常数，所以能量函数可以看作为是关于 $x_i$ 的一个二次函数，对他两次求导后得到的 $Hess ian$ 矩阵就会是一个常数矩阵。

$Hess ian$ 的主对角线上 $H_{ii}$ 系数标明了对应点 $x_i$ 受到几个力的约束，非对角线 $H_{ij}$ 则标明了 $x_i$ 与 $x_j$ 之间的受力。

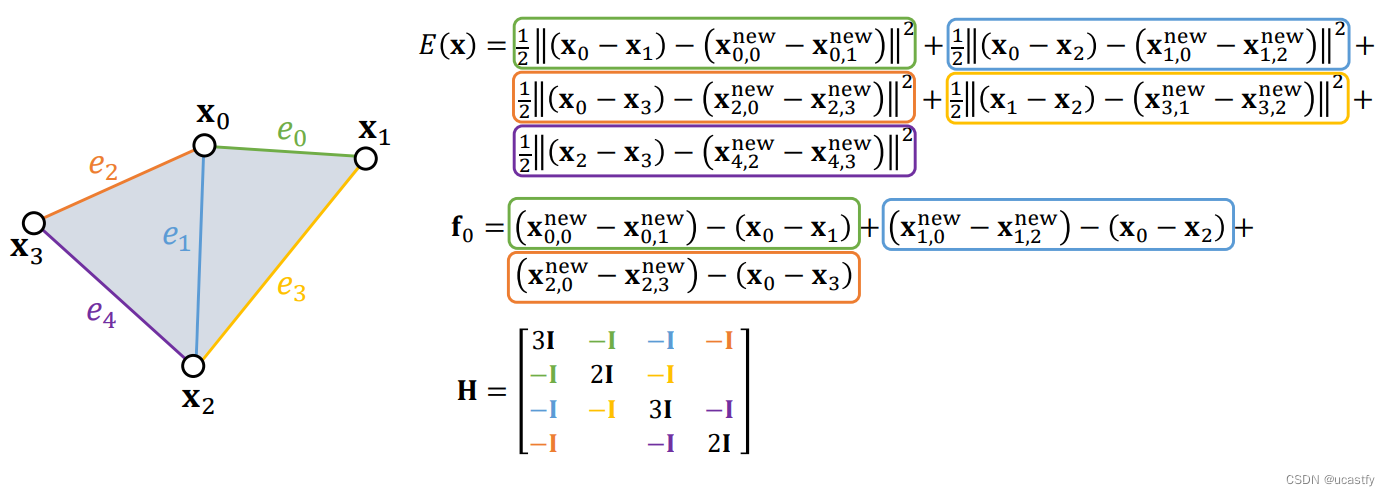
在这里插入图片描述

剩下过程和隐式积分一样，只是多了一步用约束求出新坐标（弹簧模型可以直接用弹力计算，但如果使用 shape matching 还是需要使用投影来算出新坐标），然后在求解线性系统的时候用一个常数的 $Hess ian$ 矩阵。

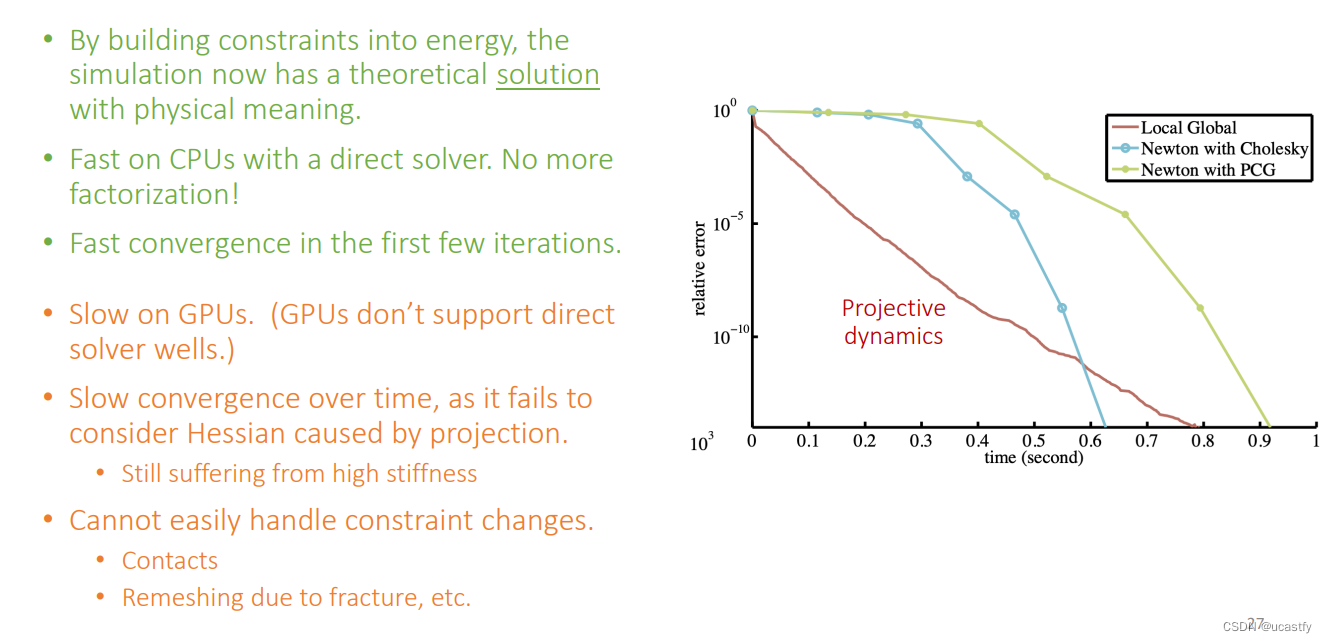
由于迭代时 $\Delta x$ 左边是个常数矩阵用 LU 分解这样的直接法来解线性系统时就只用分解一次，减少了大部分开销。

在这里插入图片描述

只要在模拟的时候保证 $Hess ian$ 矩阵是正定的，可以收敛，那么只要让实际计算的 $Hess ian$ 矩阵与标准的 $Hess ian$ 矩阵是近似的就可以，包括去掉使其不正定的部分、作业里的对角化方法或者现在变成常数正定矩阵，因此模拟的关键点在于如何让计算的 $Hess ian$ 矩阵与真实的 $Hess ian$ 矩阵靠近

在这里插入图片描述

PD 方法中变量具有物理意义，并且在初次迭代时很快，易于在CPU上实现，但是由于是直接法分解矩阵，所以不适合在GPU上并行处理，迭代次数一多性能就会下降，并且无法处理一些约束上的变化，例如接触、破碎等。

在这里插入图片描述

参考：Bouaziz et al. 2014. Projective Dynamics: Fusing Constraint Projections for Fast Simulation. TOG (SIGGRAPH).

5、Constrained Dynamics

动机：为了解决弹簧模型在弹性很大的时候，需要迭代次数很多的问题

除了用在弹簧上，还用在刚体模拟，通常用在多刚体的模拟，例如人体动画中关节之间的接触，对关节之间的距离约束很强。

照样定义弹性约束，将E个约束写成矩阵相乘，其中的 $C$ 为柔性矩阵，用弹性系数的倒数表示柔度。将 $\lambda = -C^{-1}\phi$ 定义为一个拉格朗日算子。

在这里插入图片描述

对新得到的 $f (x)$ 做隐式积分，由于 $J$ 、 $\lambda$ 都含有 $x$ ，所以与之前的单变量隐式积分不同，这里是是做多变量隐式积分。

利用动量守恒定律：
$mv_{new} - mv_{old} = f*t$
以及对 $-\phi = C\lambda$ 进行泰勒展开，通过 $\frac {\partial \phi}{\partial x}$ ， $x_{new}-x=v^{new}\Delta t$ 可以推出

在这里插入图片描述

称 $v$ 为主变量， $\lambda$ 为 $v$ 的对偶变量。

解线性系统有两种方法，直接求解得出两变量的方法称为 primal-dual 方法，但需要注意保证系数矩阵正定，否则常规方法如共轭梯度法可能用不了，需要使用特殊方法例如GMRES方法；第二种方法先求出 $\lambda_{new}$ 再求出 $v_{new}$ ，但 $\lambda_{new}$ 系数矩阵可能不好构造，也有可能比较稀疏。

Constrained Dynamics 方法好处是 $k$ 越大，它的 $C$ 越小，系统反而更稳定。因此常用于 Articulated Rigid Bodies (ragdoll animation)。

方法二对 $\lambda$ 高斯消元后得到的式子，就是一个隐式积分的式子，只不过隐式积分里面的一部分 $Hess ian$ 在高斯消元后是不存在的，把消失的东西加回去，可以增加隐式积分的稳定。

在这里插入图片描述

参考：Tournier et al. 2015. Stable Constrained Dynamics. TOG (SIGGRAPH)

总结：

在这里插入图片描述

ucastfy

关注

0
点赞
踩
5

收藏

觉得还不错? 一键收藏
0
评论
GAMES103（三）Cloth

因此我们需要设定一种数据结构来寻找内部重复的边，使用一种三元列表的结构来存储边，前两个元素存储顶点索引，第三个元素存储边所在的三角形索引，这样对边结构一排序，重复的边就会相邻，从而可以找出相邻的三角形和不重复的边。PBD方法广泛用于现在的游戏中，由于它每次对内存的访问只有一个更新后的顶点坐标，所以可以提高模型的训练速度，事实上，目前对于矩阵的计算并不是影响计算速度的瓶颈，真实的速度瓶颈还是在内存访问上。所以我们也可以推断在拉伸的时候，我们整个系统比较稳定，因为一定是正定的，但压缩的时候就有可能导致。
复制链接

扫一扫