【GAMES103学习笔记】刚体（Rigid Body）

小破站链接：https://www.bilibili.com/video/BV12Q4y1S73g?p=3
课程主页：http://games-cn.org/games103/

0 什么是刚体及刚体模拟

我们生活的空间中，存在着非常多的不会轻易变形的物体，在计算机图形学中，被称为刚体（Rigid Body）。

刚体模拟（Rigid Body Simulation）的核心目标，就是给定了物体初始状态后，根据时间的变化，求得物体的新状态。

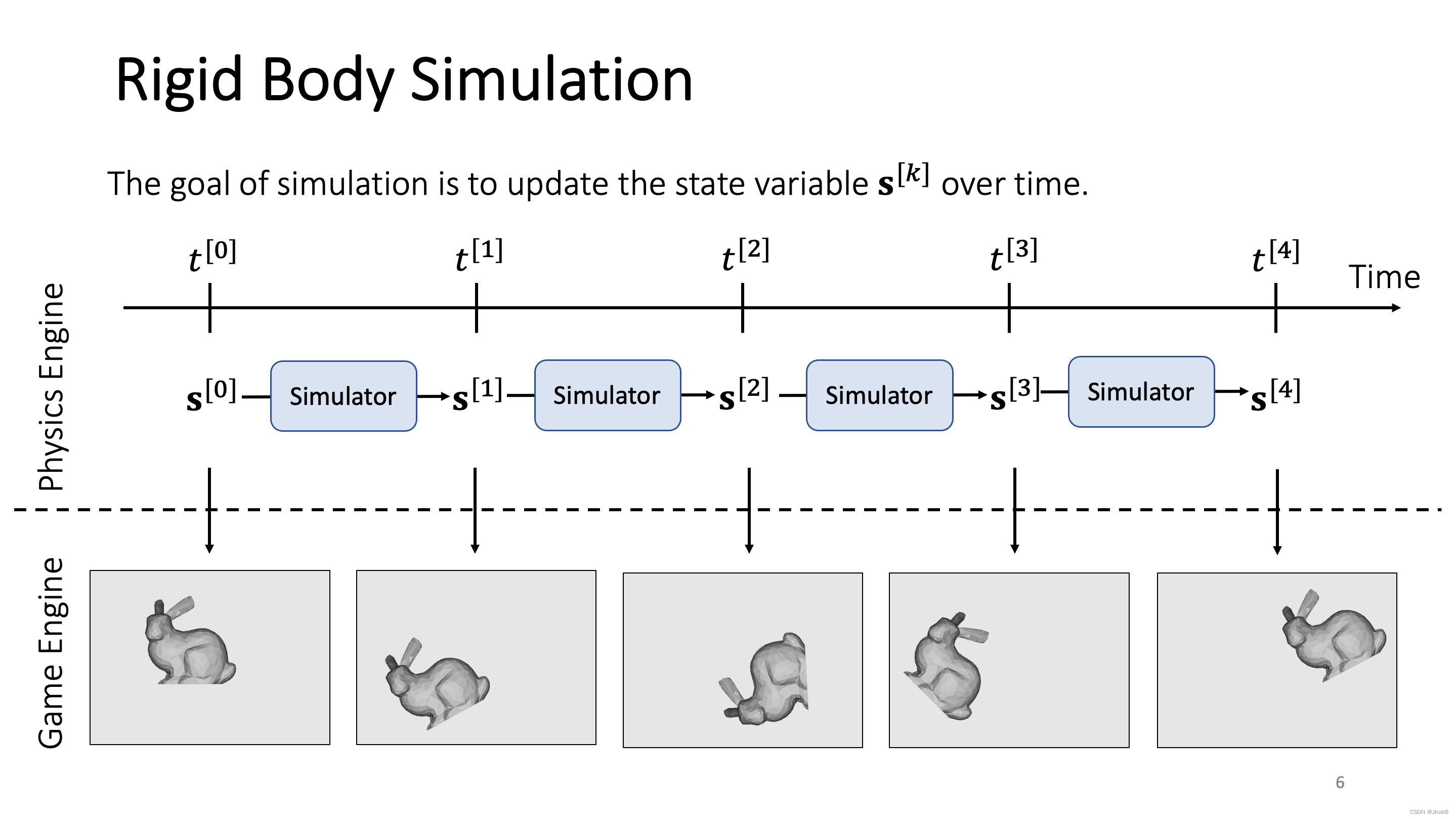
我们这里定义的刚体物体不会形变，所以刚体运动（Rigid Body Motion）只允许做平移和旋转运动。

1 平移

1.1 平移运动

平移运动（Translation Motion）的状态变量包含物体的速度$\mathbf{v}$和物体的位置$\mathbf{x}=[x,y,z]$。

1.1.1 速度

上图公式的第一行描述了速度如何随着时间的变化而变化。

$t^{[1]}$时刻的新的速度$\mathbf{v}$等于$t^{[0]}$时刻的速度$\mathbf{v}$加上加速度。

后面这一串就是在求加速度${\mathbf{M}}^{-1}{\int }_{t^{[0]}}^{t^{[1]}}f(\mathbf{x}(t),\mathbf{v}(t),t)dt$。

根据牛顿第二定律，加速度等于力除以质量。这里的计算力的写成了位置、速度还有时间的函数$f(\mathbf{x}(t),\mathbf{v}(t),t)$，考虑到现实世界中物体的受力比较复杂，因此写的也比较复杂。

1.1.2 位置

上图公式的第二行描述了位置如何随着时间的变化而变化。

$t^{[1]}$时刻新的位置$\mathbf{x}$等于$t^{[0]}$时刻的位置$\mathbf{x}$加上速度对时间的积分。

透过上述两个公式可以看到，解刚体的模拟方程，就是在解公式中的积分；又因为都是对「时间」这个参数的积分，因此也称时间积分。

1.2 时间积分

在基于物理模拟的计算机图形学中，我们会经常看到这个词。

要想在计算机中解决积分，肯定不会是使用牛顿-莱布尼茨公式求原函数来求解。

回想定积分的物理含义，他是一条曲线段被积分的上下限截断，与x轴围成的面积。

根据这个原理，当$\Delta t$足够小的时候，计算一个小矩形的面积，当做积分结果对积分进行估算。

我们既可以采用积分的下限去估算面积，也可以采用积分的上限去估算面积，甚至是上限和下限的中点。

这就产生了计算机中解时间积分的三个常用的方法：显示欧拉（Explicit Euler）、隐式欧拉（Implicit Euler）和中点法（Mid-point）。

这里面最准确的是中点法。

1.3 半隐式欧拉

回到平移的积分公式，这里面有两个积分“嗷嗷待解”。这里我们采用显示欧拉与隐式欧拉结合的方式求解。

求解速度的时候采用显示欧拉，使用积分下限；求解位置的时候用隐式欧拉，使用积分上限。

在有些文献中，称这个方法为半隐式欧拉（Semi-implicit Euler）。他有另一个比较有趣的名字，叫做Leapfrog Integration。

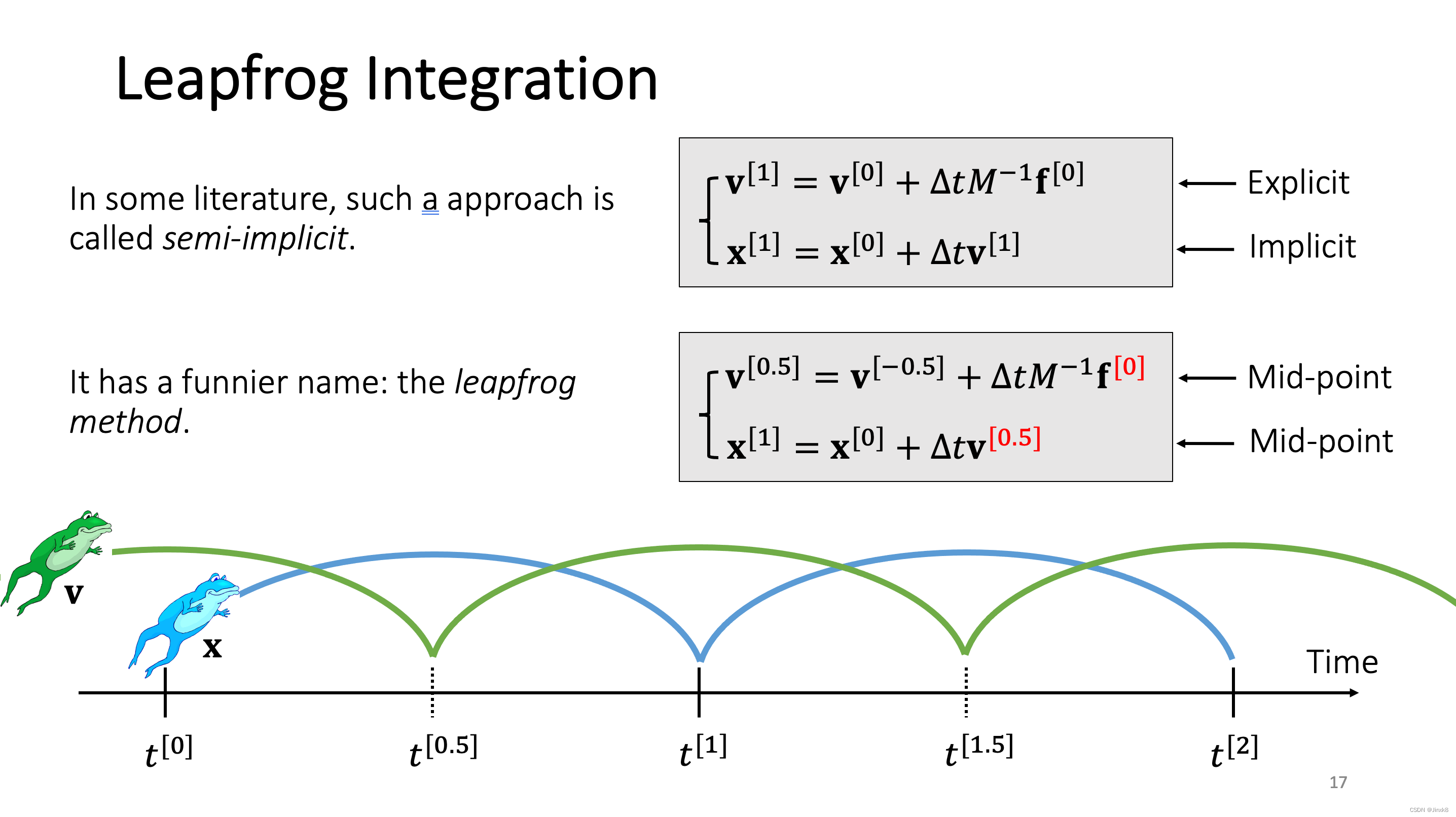
有了这样的迭代的更新方法，我们就可以在计算机中进行模拟了。

1.4 力的分类

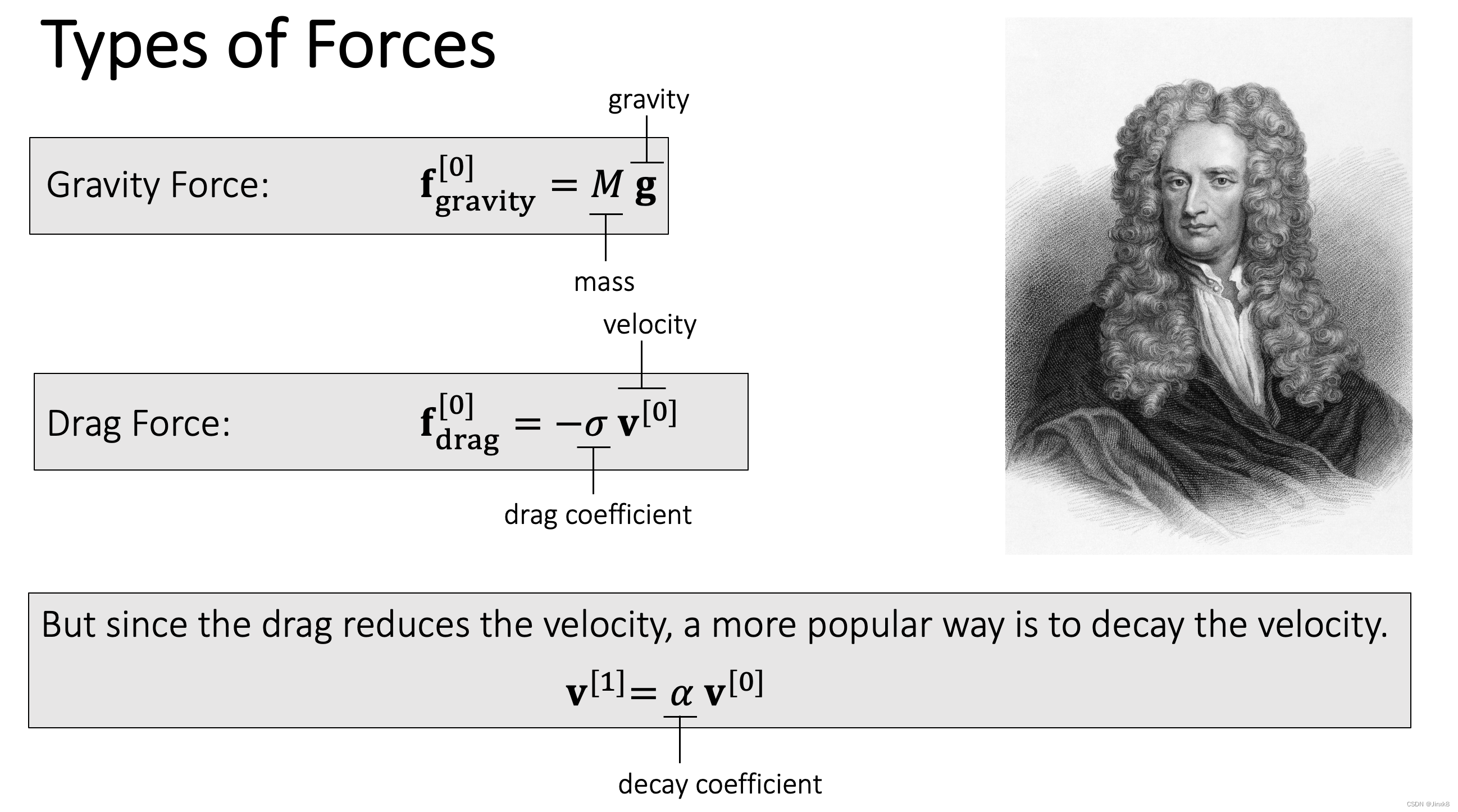
最后一条的意思是模拟Drag Force可以对速度做一个衰减来简单的实现。乘一个$\alpha$，例如$\alpha =0.99$。

2. 旋转

2.1 采用什么状态参数描述旋转

不用旋转矩阵，太复杂且有多余的信息。

不用欧拉角，有万向节死锁问题（这个up主讲的不错，和别人讲的不一样）。

采用四元数（Quaternion）。

2.2 四元数

2.2.1 什么是四元数

四元数（Quaternion）的发明是想用复数系统来描述三维空间中的一个点。之所以会有这个想法是因为3D空间中的一个点如果仅仅用xyz坐标表示，是无法定义除法运算的。

发明了四元数后就可以定义了，四元数之间的乘法和除法可以用下图的乘法表来描述。

一个四元数$q$由两部分组成，实数部分$s$和虚数部分$v$，$q=[s\mathbf{v}]$。$v$是一个3D向量，代表$ijk$。四元数与四元数之间的运算如下图。

2.2.2 四元数与旋转

一个物体绕一个轴$v$旋转$\theta$度，写成四元数的形式如下图所示。

我们给四元数添加了一个约束$\Vert q\Vert =1$，即$v$的模长为1。因为实数部分$s=cos\frac{\theta }{2}$，所以导出$\Vert v{\Vert }^2=si{n}^2\frac{\theta }{2}$。

把一个四元数转换成矩阵，记住公式即可。下图中$xyz$是四元数的三个虚部。

为什么只用一个轴和一个角度表示成的四元数就表示了三维空间中的所有旋转呢？欧拉角可是有三个数啊！

仔细想想，当我们只观察旋转的起始状态和终止状态时，似乎真的只让某个物体绕着某个轴旋转一下即可。

2.3 旋转运动

接下来的我们要用四元数来模拟旋转运动（Rotation Motion）。旋转运动的状态变量包含角速度$\omega$和描述旋转的四元数$\mathbf{q}$。

旋转运动的公式如下：

$$\begin{array}{rl}{\omega }^{[1]}& ={\omega }^{[0]}+\Delta t({\mathbf{I}}^{[0]}{)}^{-1}{\tau }^{[0]}\\ {\mathbf{q}}^{[1]}& ={\mathbf{q}}^{[0]}+[0\frac{\Delta t}{2}{\omega }^{[1]}]\times {\mathbf{q}}^{[0]}\end{array}$$

这里面有不认识的$\mathbf{I}$、$\tau$，我们接下来逐步讲解。

2.3.1 角速度

除了知道如何用四元数表示旋转，我们还需要知道单位时间旋转的速率，即旋转对于时间的导数，用于求解当力作用于物体上时，物体将如何旋转。

这里我们用一个3D向量$\omega$来表示。$\omega$的方向表示旋转轴的方向，$\omega$的大小表示旋转的速率。

这里在更新角速度的时候，不能简单的使用牛顿第二定律了。对于旋转运动而言，我们需要知道力矩（Torque）和惯量（Inertia）。

2.3.1.1 力矩

计算力矩使用如下公式。

假设物体的质心为局部空间原点，物体上的一个受力点${\mathbf{r}}_i$受力${\mathbf{f}}_i$后，变成了$\mathbf{R}{\mathbf{r}}_{\mathbf{i}}$（$\mathbf{R}$为旋转矩阵）。那么该点所受的力矩为$\mathbf{R}{\mathbf{r}}_{\mathbf{i}}$与${\mathbf{f}}_i$的叉积。

$${\tau }_{\mathbf{i}}=(\mathbf{R}{\mathbf{r}}_{\mathbf{i}})\times {\mathbf{f}}_{\mathbf{i}}$$

接下来对所有顶点求和，得到物体整体的力矩。

$$\tau =\sum {\tau }_{\mathbf{i}}$$

2.3.1.2 惯量

惯量的计算方法，记公式吧。

首先计算一个reference状态下的Inertia矩阵${\mathbf{I}}_{\mathbf{ref}}$。

$${\mathbf{I}}_{\mathbf{ref}}=\sum {\mathbf{m}}_{\mathbf{i}}({\mathbf{r}}_{\mathbf{i}}^{\mathbf{T}}{\mathbf{r}}_{\mathbf{i}}1-{\mathbf{r}}_{\mathbf{i}}{\mathbf{r}}_{\mathbf{i}}^{\mathbf{T}})$$

为了避免和$\mathbf{I}$搞混，这里粗体的$1$就是个单位矩阵。

上述求出的${\mathbf{I}}_{\mathbf{ref}}$是一个3x3的矩阵。

然后使用物体的旋转矩阵，求得物体旋转后的Inertia。

$$\mathbf{I}=\mathbf{R}{\mathbf{I}}_{\mathbf{ref}}{\mathbf{R}}^{\mathbf{T}}$$

2.3.1.3 小结

有了$\tau$和$\mathbf{I}$，就能看懂旋转运动的第一条公式了。

$$\begin{array}{rl}{\omega }^{[1]}& ={\omega }^{[0]}+\Delta t({\mathbf{I}}^{[0]}{)}^{-1}{\tau }^{[0]}\end{array}$$

2.3.2 四元数

第二条公式比较简单，就是更新表示物体旋转的四元数的数值。

$$\begin{array}{rl}{\mathbf{q}}^{[1]}& ={\mathbf{q}}^{[0]}+[0\frac{\Delta t}{2}{\omega }^{[1]}]\times {\mathbf{q}}^{[0]}\end{array}$$

这里需要注意，$[0\frac{\Delta t}{2}{\omega }^{[1]}]$和${\mathbf{q}}^{[0]}$中间的乘号不是向量叉乘，是四元数的乘法，定义在四元数的乘法表中。

$[0\frac{\Delta t}{2}{\omega }^{[1]}]$的实数部分是0，后面是由角速度$\omega$计算得到的虚数部分。

最后，最好再将${\mathbf{q}}^{[1]}$归一化一下。

3 刚体运动小结

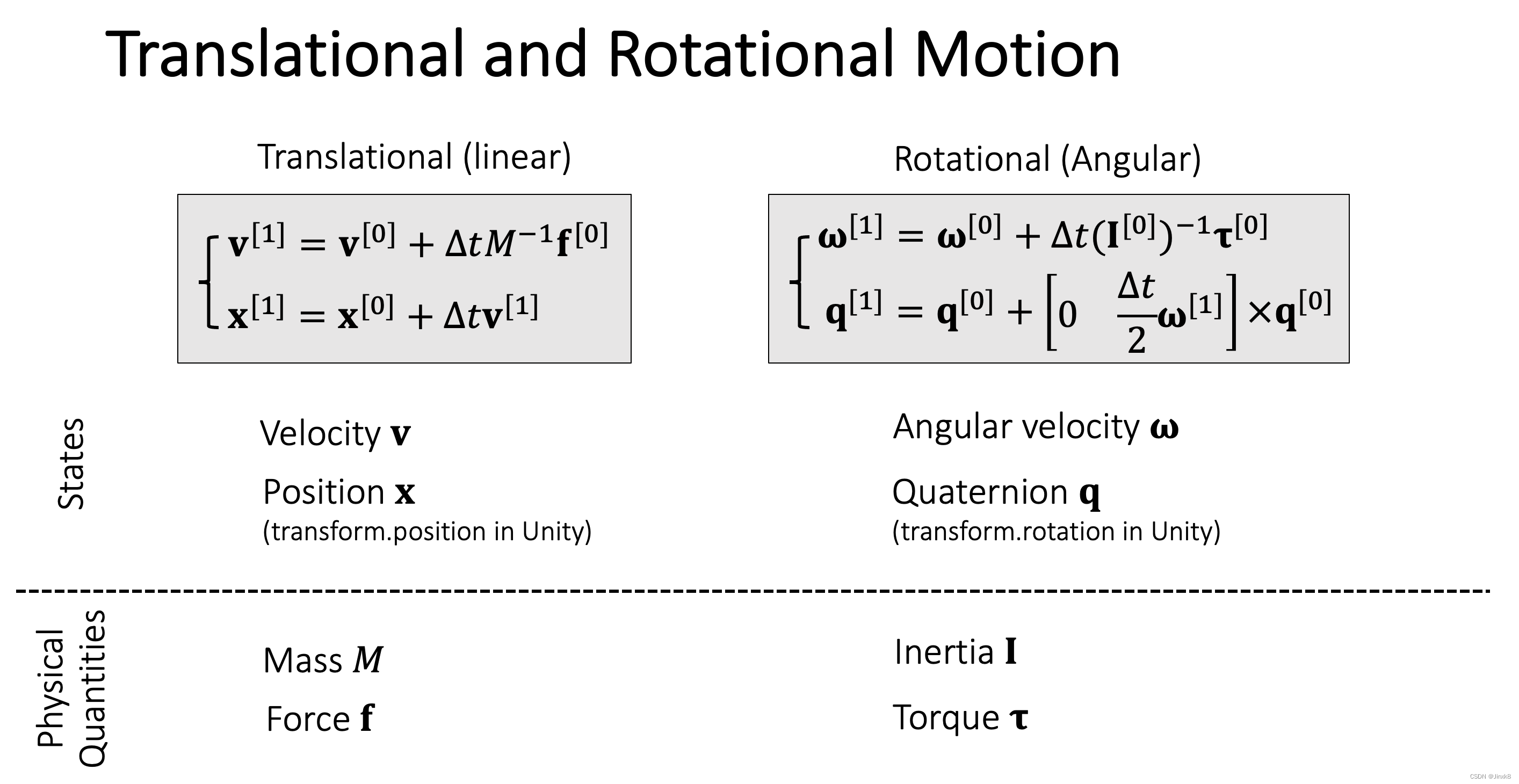
状态变量有四个，速度$\mathbf{v}$，位置$\mathbf{x}$，角速度$\mathbf{w}$，旋转四元数$\mathbf{q}$。

还有一些物理的中间变量，质量$\mathbf{M}$，作用于每个质点上的力${\mathbf{f}}_i$以及合力$\mathbf{f}$，惯量$\mathbf{I}$，力矩$\tau$。

还有需要注意的就是重力不产生力矩，如果要模拟的系统没有重力以外的力，可以不用更新$\mathbf{w}$。