在日常的生产生活中人们使用的电子功率放大器一般分为线性功率放大器和非线性功率放大器两大类。其中线性功率放大器易于实现,不会产生除信号外的其它频率成分,具有高保真的特点,但是它的缺点就是效率底下,在大功率的时候需要加装大面积的散热片来进行散热,这样不利于体积小型化。而非线性功放是要将输入的信号进行调制,因此产生了一些除了信号本身外其它的频率成分,而这些频率成分一般都是高于信号本身的频率的,因此需要在功放的输出端进行低通滤波处理,它的优点是效率很高理论上可达100%实际的也能达到80%以上,因此在大功率的情况下体积也可以做的很小,在一般的对信号质量要求不是过分高的场合它是首选。
功率放大器还可以分为Class-A, Class-AB,Class-B, Class-C, Class-D, Class-E, Class-F, Class-G, Class-H, Class-S等。其中Class-D最为常用,它属于非线性功放。Class-A, Class-AB, Class-B次之。其它的在一些特殊的场合才会使用到。
Class-A
此类功率放大电路的静态工作点Q通常固定在交流负载线重点,功放管在输入信号整个周期内都有不失真的电流输出,信号的正、负半周功放电路都处于放大状态。甲类功放静态电流大,功率损耗大,效率低;在没有信号输入时,功率损耗最大,理想效率只有50% 。该类功放的非线性失真很小,因此常见于音频高保真功放电路。
Class-B
此类功率放大电路的静态工作点Q在横轴(Ic = 0)上,其特点是在输入信号的整个周期内,功率管只在半个周期内导通,另半个周期截止,无静态电流,因此,没有输入信号时,电源不消耗功率,效率高,理想效率可达78.5%。此类功放通常工作在推挽方式下,由于三极管都存在一个导通角,小于导通角时上下两个功放管都不工作,出现交越失真。
Class-AB
此类功放的静态工作点在class–A和class-B之间,靠近截止区,在输入信号的一个周期内,功放管导通时间大于半个周期,静态电流小,效率较高,但电流波形失真较大。实际上,AB类并不能真正算一类,它只是A和B的结合。如果一个A类功放偏入B类,那么偏得更多些就变成了AB类。AB类的线性度比A类和B类差,有观点认为,AB类功放唯一合理的用处在于使A类功放在低负载阻抗下也能够继续合理工作。
Class-D
此类功放的功放管工作在开关状态,即饱和和截止两种极端工作状态,因此不用关心功率管的线性性能,可由数字信号控制功率管的通断。
功率管通常使用MOSFET管,当功放管工作在开关状态时,理想情况下功放管导通时内阻为零,截止时内阻无穷大,效率是100% 。通常在导通状态下功率管的导通内阻很小,远小于功放管的负载,因此功耗小、效率高,实际达到的效率通常都高于80%。
信号源的形式采用方波,控制方波的宽度可以改变信号的幅度(PWM)。
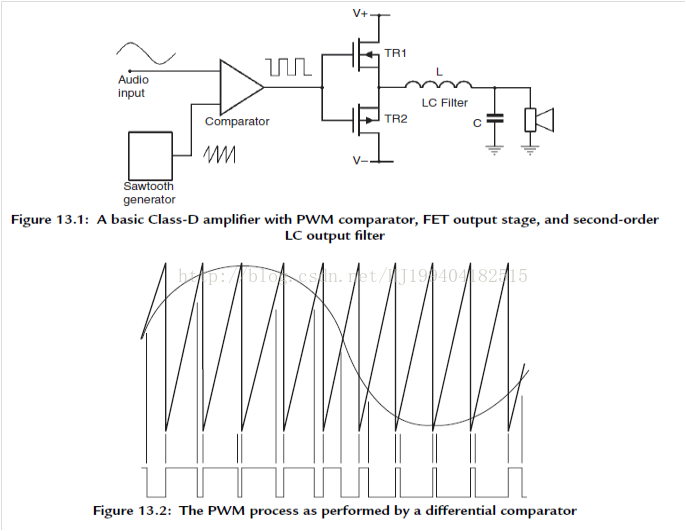
下图是D类功放实现的电路结构及信号调制方式:
经过调制的信号表达式为:
由上式可知,PWM信号的频谱有三部分组成:调制信号的频谱,载波信号的频谱及调制信号与载波信号相互作用而产生的边带信号。其中,角频率为ω的基波信号以及角频率为ω-Ω的边带信号对调制信号的滤出影响较大。当ω≫Ω时,可以减少调制信号的失真。
Matlab仿真
下面给出的是按照上述原理实现的PWM调制仿真代码:
close all;
clear all;
clc;
fs = 56e5; %采样率
Ts = 1/fs; %采样周期
f_tri = 28e4; %三角波频率
T_tri = 1/f_tri; %三角波周期
f0 = 28e3; %CW信号频率
T0 = 1/f0; %CW信号周期
Time_len = 100*T0; %采样总时长
nTs = 0:Ts:(Time_len-Ts); %采样时刻
num = size(nTs,2);
nFs = (0:num-1)*fs/num;
%%
%生成待调制信号
y_original = sin(2*pi*f0*nTs);
%生成三角波数据
y_tri = 1.5*Triangle_Wave_Generate(fs,f_tri,Time_len);
%生成调制信号
y_modulation = zeros(size(y_original));
y_modulation(1:end) = -1;
set = find(y_original>y_tri); %找出大于三角波值的位置
y_modulation(set) = 1;
figure;
plot(nTs,y_original,'b',nTs,y_tri,'g',nTs,y_modulation,'r-*');
legend('原始信号','三角波','调制的PWM');
title('时域波形');
%%
num1 = 1*num; %fft点数
nFs1 = (0:num1-1)*fs/num1; %频谱坐标
abs_fft_y_original_num1 = abs(fft(y_original,num1));
abs_fft_y_tri_num1 = abs(fft(y_tri,num1));
abs_fft_y_modulation_num1 = abs(fft(y_modulation,num1));
max_abs_fft_y_original_num1 = max(abs_fft_y_original_num1);
max_abs_fft_y_tri_num1 = max(abs_fft_y_tri_num1);
max_abs_fft_y_modulation_num1 = max(abs_fft_y_modulation_num1);
max_abs_fft_y = max([max_abs_fft_y_original_num1,max_abs_fft_y_tri_num1,max_abs_fft_y_modulation_num1]);
figure;
plot(nFs1,abs_fft_y_original_num1/max_abs_fft_y,'b',nFs1,abs_fft_y_tri_num1/max_abs_fft_y,'g',nFs1,abs_fft_y_modulation_num1/max_abs_fft_y,'r');
legend('原始信号','三角波','调制的PWM');
title('归一化的频域波形');
axis([0,5*f_tri,0,1]);
%%
%恢复波形
%********************** FIR低通滤波器系数 Fpass=28KHz Fstop=280KHz fs=5.6MHz 32阶
hn = [0.0097 0.0076 0.0103 0.0133 0.0168 0.0205 0.0244 0.0284 0.0324 0.0363 0.0400 0.0434 0.0463...
0.0487 0.0505 0.0516 0.0519 0.0516 0.0505 0.0487 0.0463 0.0434 0.0400 0.0363 0.0324 0.0284...
0.0244 0.0205 0.0168 0.0133 0.0103 0.0076 0.0097];
LPF_y_modulation = filter(hn,1,y_modulation);
abs_fft_LPF_y_modulation = abs(fft(LPF_y_modulation,num1));
figure;
plot(nTs,y_original,'b',nTs,y_modulation,'r-*',nTs,LPF_y_modulation,'g-*');
legend('原始信号','调制的PWM','恢复的信号');
title('时域波形');
figure;
plot(nFs1,abs_fft_y_original_num1/max_abs_fft_y,'b',nFs1,abs_fft_y_modulation_num1/max_abs_fft_y,'r-*',nFs1,abs_fft_LPF_y_modulation/max_abs_fft_y,'g-*');
legend('原始信号','调制的PWM','恢复的信号');
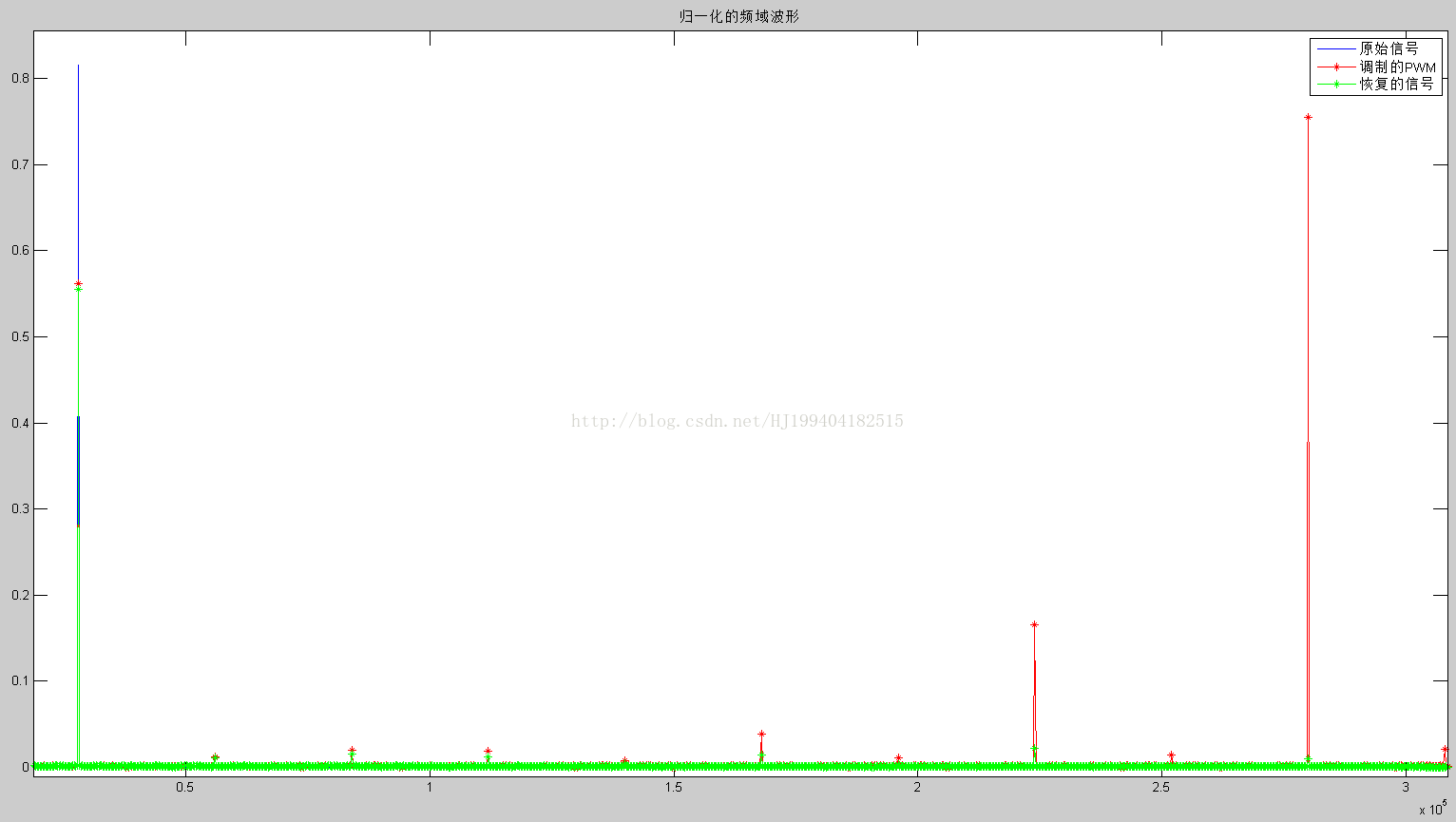
title('归一化的频域波形');
axis([0,5*f_tri,0,1]); function y = Triangle_Wave_Generate(fs,f0,Time_len)
%******************triangle wave generate function*************************
%****Input parameter specification****
% fs Sample rate Unit:Hz
% f0 Frequency of triangle wave Unit:Hz
% Time_len The length of sample time Unit:s
%****Output parameter specification****
% y the result of funcion
%**************************************************************************
% Time of last update 20171102
% Update note write for the first time
%%
Ts = 1/fs; %Sampling period
T0 = 1/f0; %Period of triangle wave
k = 4/T0; %Absolute value of slope(斜率)
nTs = 0:Ts:(Time_len-Ts);
num = size(nTs,2);
y = zeros(1,num);
for i=1:num
cycle = fix(nTs(i)/T0); %求当前所在的周期数
t = nTs(i) - cycle*T0; %把时间限定在[0,T0)内
if t<T0/4
y(i) = k*t;
elseif t<T0*3/4
y(i) = -k*(t-T0/2);
else
y(i) = k*(t-T0);
end
end
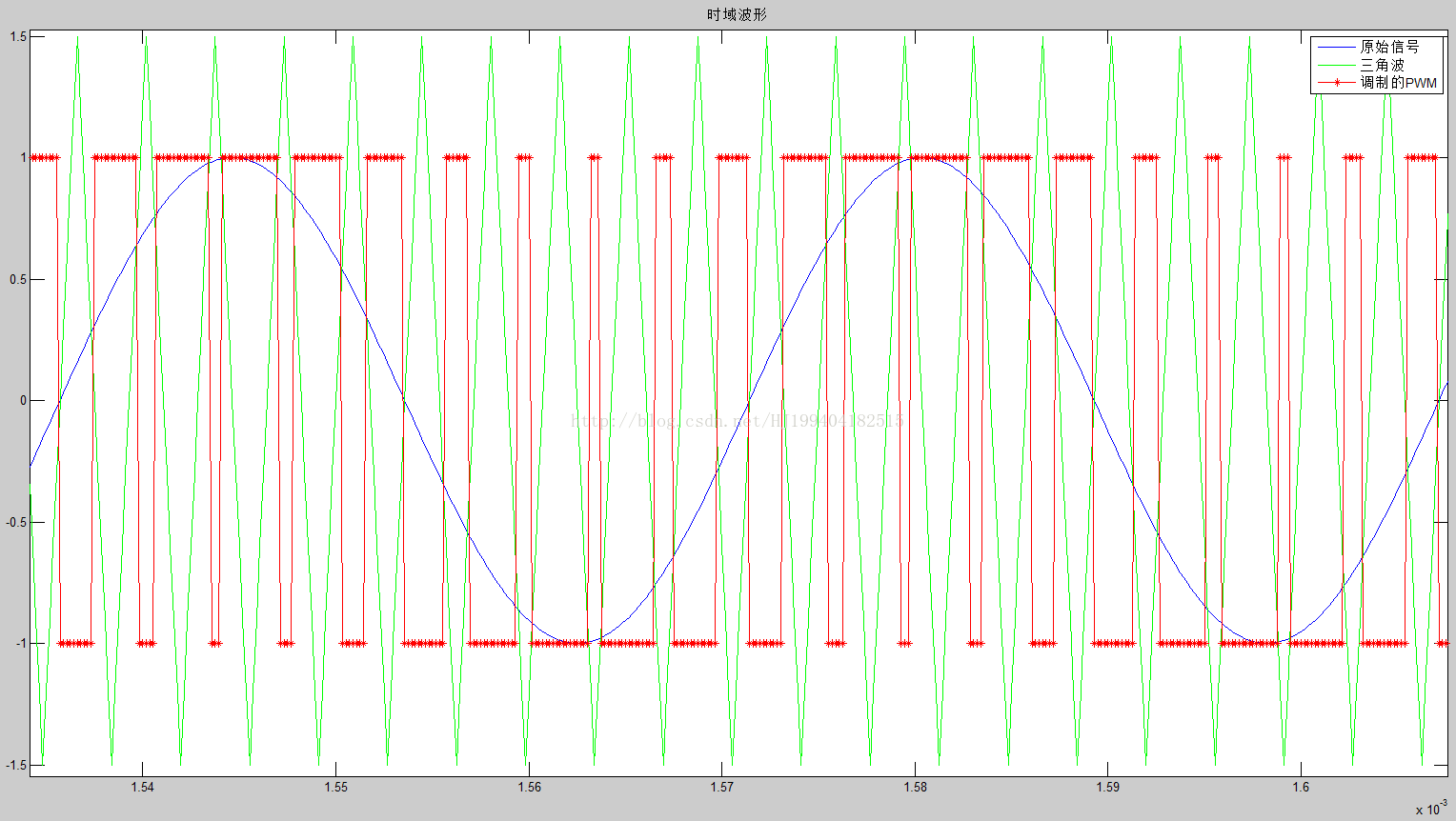
将局部放大如下图所示:
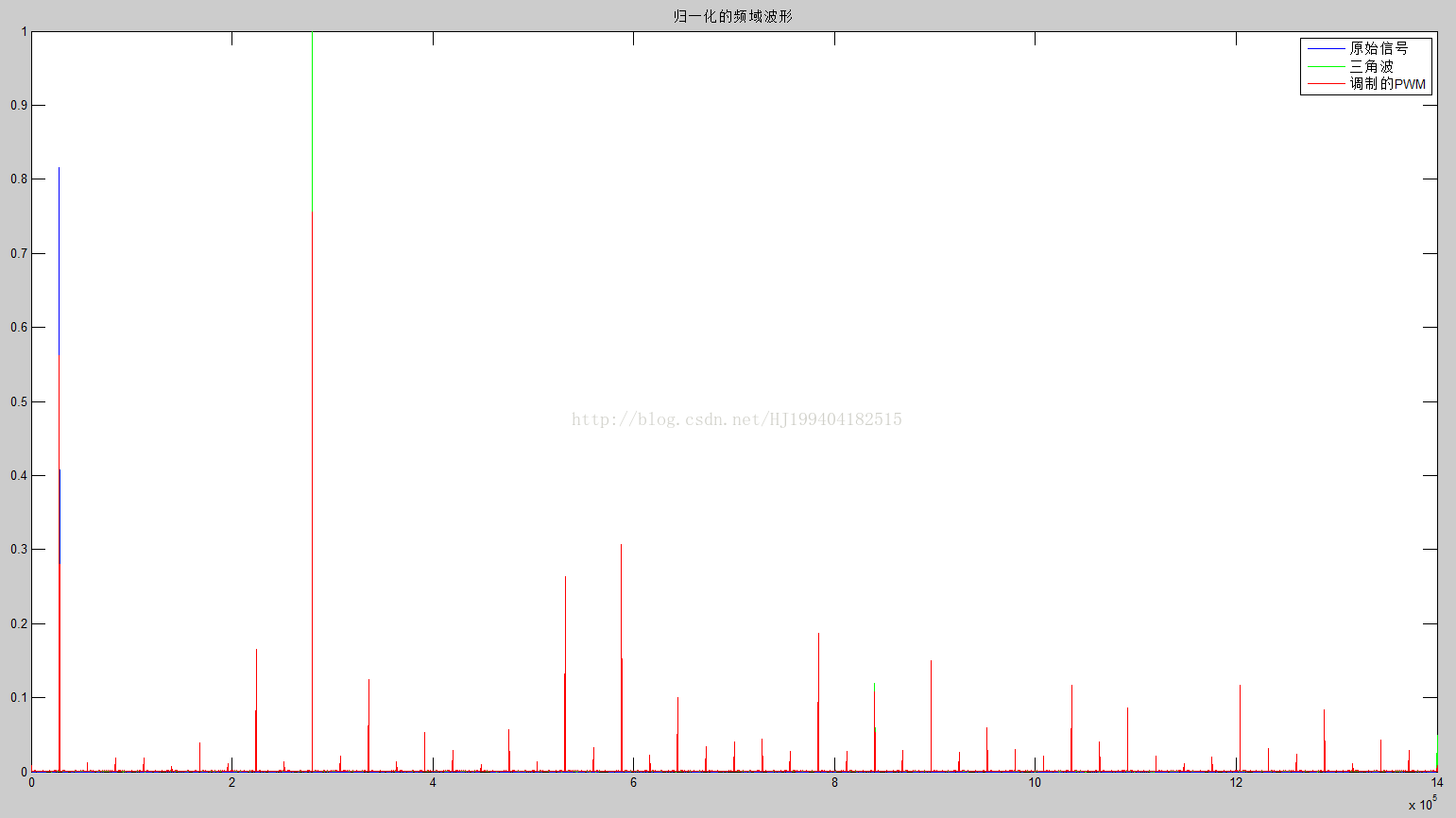
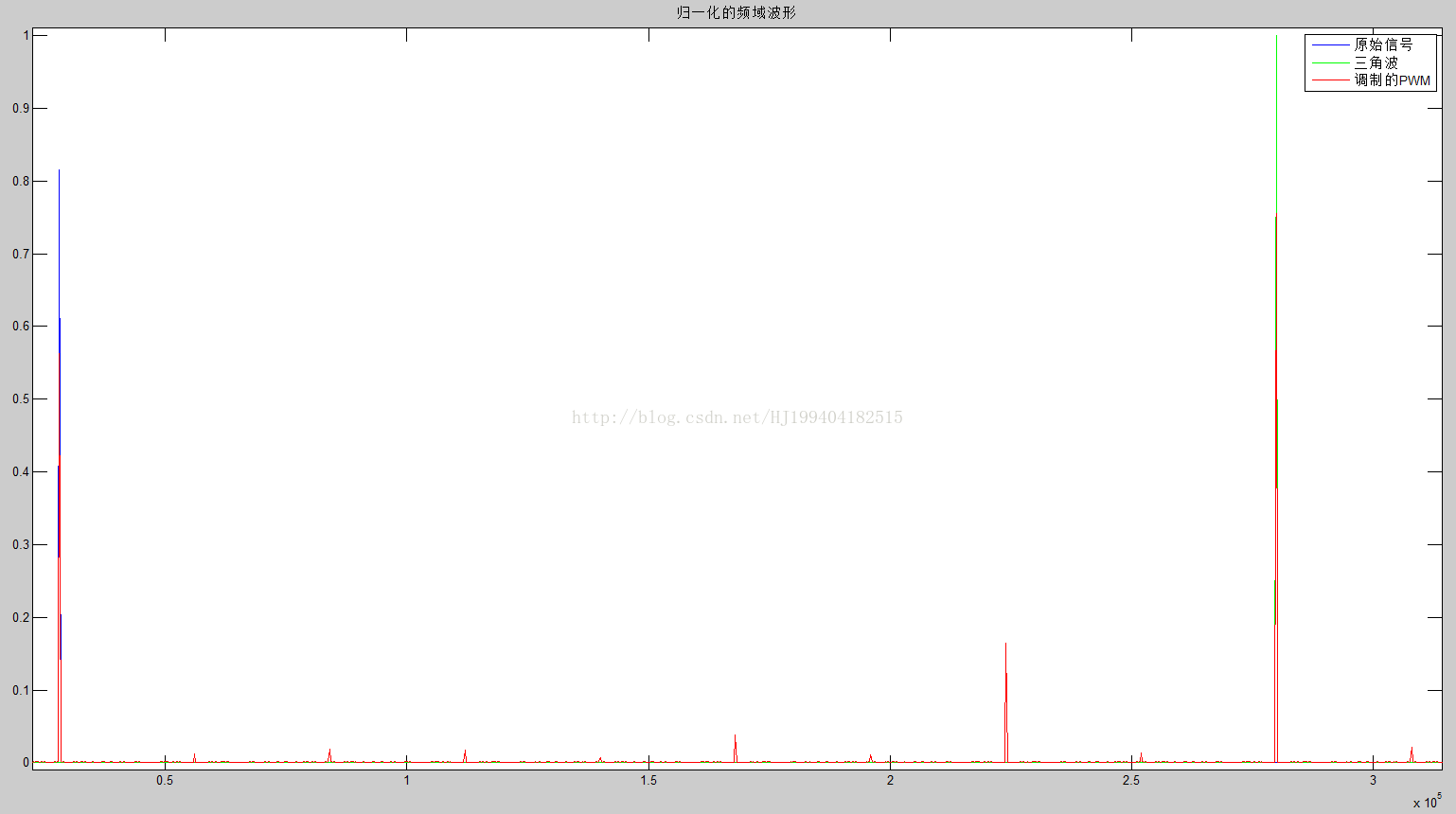
第二图是其频谱:
将低频部分放大如下图所示:
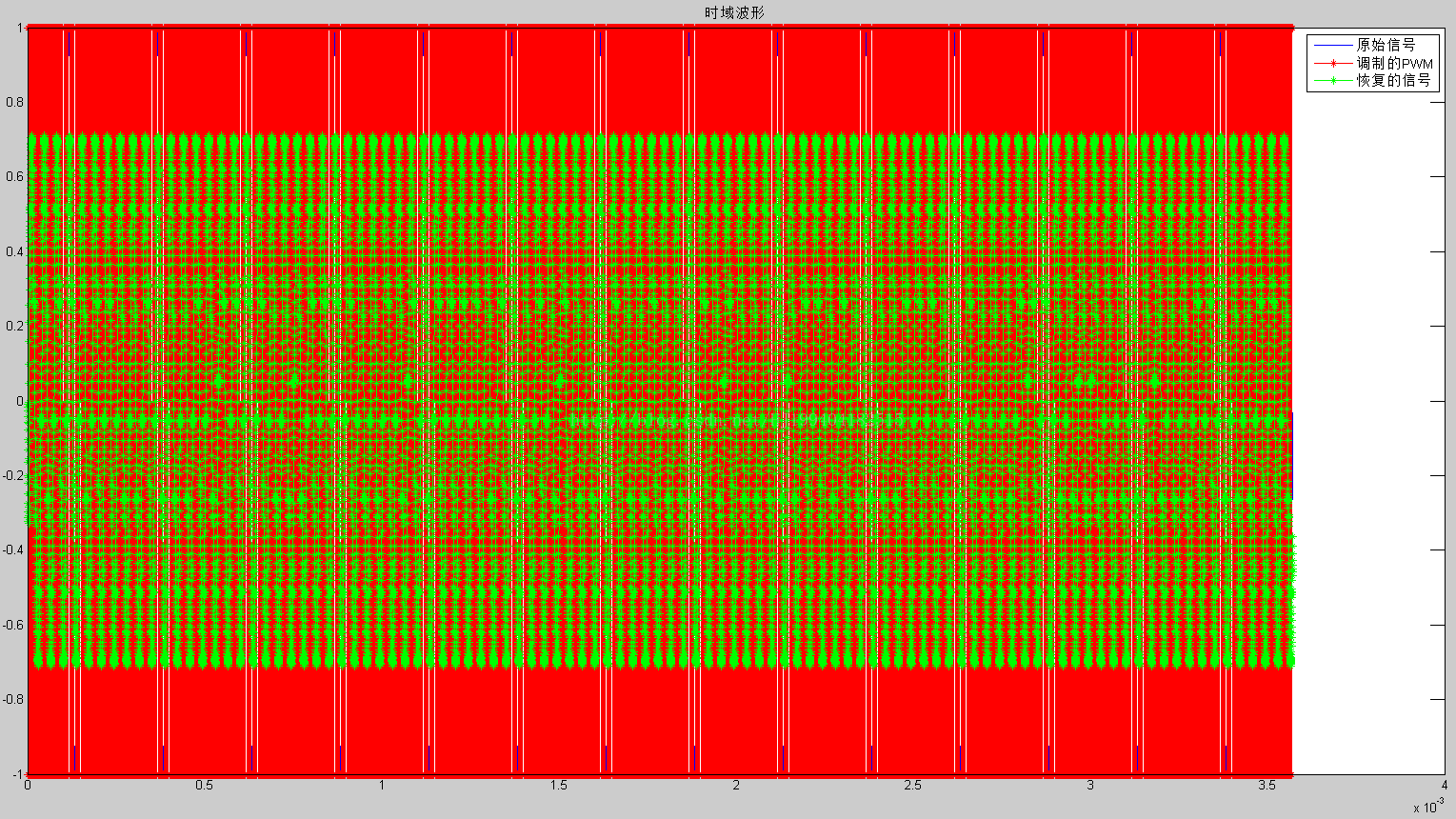
第三张图是模拟低通滤波器滤波后的时域图:
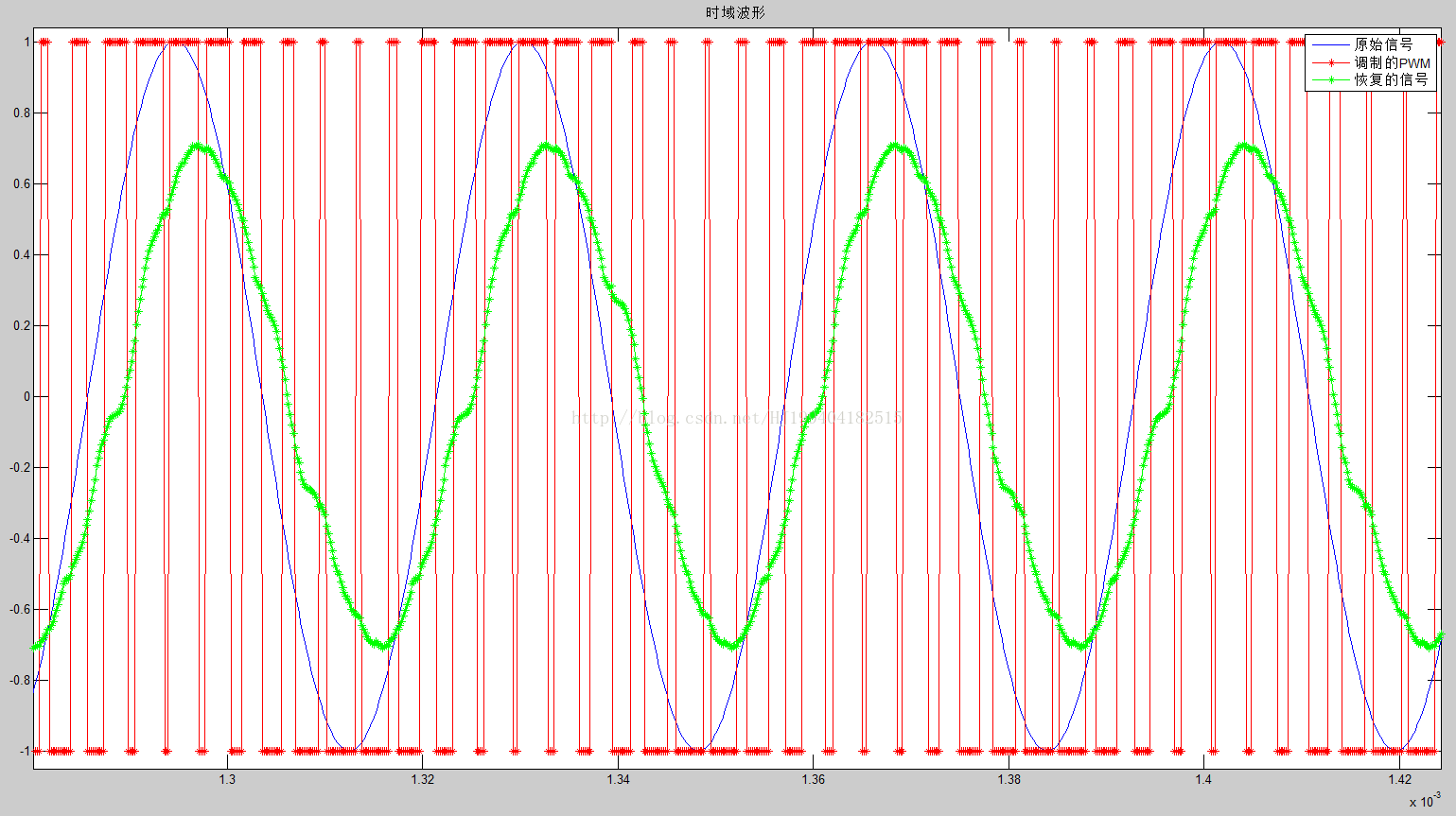
局部放大如下图:
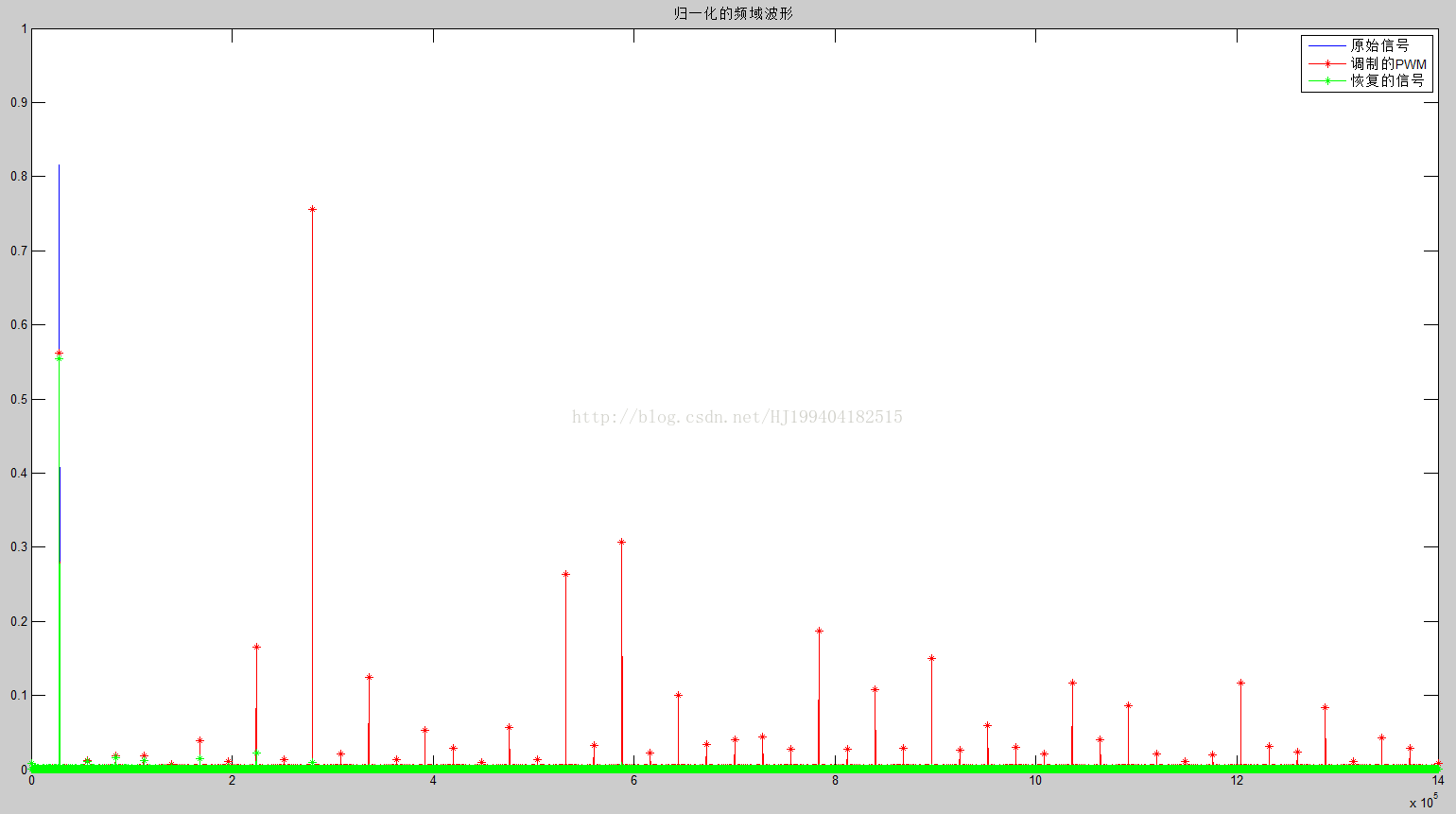
可以看到绿色的部分就是恢复的波形,第四张是其对应的频谱:
将低频放大如下图所示:
可以看到绿色部分的频谱和蓝色的频谱基本一致,如果想要更好的滤波效果可以使用阶数更高的滤波器,然而阶数越高所需要的滤波元件越多,体积也就越大,而一般的负载都是一个低通滤波器因此输出的滤波可以不用使用阶数太高的滤波器,甚至有的时候可以不用使用,直接利用负载本身的低通滤波器特性对波形进行滤波。










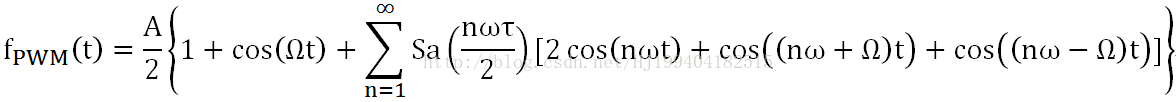
















 604
604

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










