Minimax and Biobjective Portfolio Selection Based on Collaborative Neurodynamic Optimization
基于协同神经动力学优化的极大极小双目标投资组合选择
文章目录
一. 基本信息
Author
- Man-Fai Leung , Member, IEEE
- 梁文辉(IEEE会员)于2019年从香港城市大学获得计算机科学博士学位。目前,他就职于香港香港开放大学科学与技术学院。他目前的研究兴趣包括投资组合优化、多目标优化和计算智能。(基于2021年7月14日发表的文件)。
- Jun Wang , Fellow, IEEE
- 王军(IEEE 终身院士)获得理学学士学位电气工程学位和硕士学位分别于1982年和1985年在大连理工大学获得系统工程学士学位,并于1985年在大连理工大学获得博士学位。 1991年获得美国俄亥俄州克利夫兰凯斯西储大学系统工程博士学位。凯斯西储大学;北达科他大学,美国北达科他州大福克斯;和香港中文大学。他还在美国俄亥俄州代顿市的美国空军阿姆斯特朗实验室担任过各种短期或兼职访问职位; RIKEN脑科学研究所,东京,日本;华中科技大学,武汉,中国;和上海交通大学,中国上海。现任香港城市大学计算机科学系及数据科学学院讲座教授。(基于 2023 年 4 月 4 日发布的文件)。
Abstract
投资组合选择是金融投资中的重要问题之一。本文研究了基于协同神经动力学优化的投资组合选择。将经典的马科维茨(Markowitz)均值方差(MV)框架及其变体均值条件风险值(CVaR)表述为极小极大和双目标投资组合问题。然后应用神经动力学方法求解这些优化问题。对于每个问题,多个神经网络协同工作,通过基于**粒子群优化(PSO)**的权值优化来表征有效边界。基于四个主要市场股票数据的实验结果显示了协同神经动力学方法在组合优化问题上的性能和特点。
Index Terms
-
Conditional value-at-risk 条件风险值
-
mean–variance (MV) 均值方差
-
minimax optimization 极大极小优化
-
multiobjective optimization 多目标优化
-
neurodynamics 神经动力学
-
portfolio selection 投资组合选择
专有名词缩写:
- MV:mean–variance
- CVaR:conditional value-at-risk
- PSO:particle swarm optimization
二. 论文正文
I. INTRODUCTION
作为现代金融的基石,至少有五位诺贝尔奖得主[1]-[5]的著作涉及到投资组合选择或优化问题。从学术和经济的角度来看,投资组合选择或优化是金融投资领域的重要问题(参见[6]-[13]及其参考文献)。
投资组合优化是一种通过分散低预期业绩可能导致的损失风险来优化一组金融工具以获得高预期收益的重要方法。
自诺贝尔奖得主Markowitz的开创性工作以来[1],均值-方差(MV)优化成为资产配置的经典方法[6]。这项工作介绍了三个主要的重要概念:
- 多样化,以尽量减少投资组合的风险;
- 用统计方法对投资组合的风险和收益进行量化;
- 同时考虑风险和收益,以达到最优权衡。
在文献中,有许多结果可用于投资组合优化。将投资组合问题重新表述为单目标优化问题是研究方向之一:
- 最小化特定投资组合预期收益水平下的风险函数,或最大化特定风险水平下的投资组合预期收益(见[1],[14]-[17]),
- 最大化投资组合的夏普比率(期望收益除以收益的标准差)[3],[18],
- 基于风险参数优化最小化最坏情况下可能损失的minimax模型[19]-[21]等。
通过对其中一个优化问题进行优化,生成一个有效的解,该解表示每个资产在集合中投资的比例。
此外,投资组合选择也可以同时将风险函数最小化和投资组合预期收益最大化表述为一个双目标优化问题[22],[23],并通过优化优化问题生成一组最优资产配置。尽管有大量的研究,但通过实时机制开发计算智能方法来优化投资组合是非常可取的。在这种情况下,由于信息处理的并行性和分布性,神经动力学方法能够胜任投资组合选择。
多目标优化涉及在一组约束条件下,同时优化至少两个相互冲突且不相称的目标函数。它可以在各个领域找到,包括商业和工程[22],[24]-[26]。与寻找单个最优解的单目标优化不同,多目标优化的目的是生成一组有效解,称为有效边界或帕累托边界(an efficient frontier or a Pareto frontier)[27]。
自Hopfield和Tank[28],[29]的开创性工作以来,神经动力学优化作为一种受生物学启发的方法出现(参见[30]-[34],以及其中的参考文献)。许多神经网络模型可用于解决各种优化问题,如伪凸优化 pseudoconvex optimization[35]、非光滑逆优化nonsmooth invex optimization[36]、二次双层优化 quadratic bilevel optimization[37]、[38]、全局优化global optimization[39]、[40]等。
近年来,神经动力学优化方法得到了极大极小和多目标优化的扩展。例如,提出了一种神经网络[41]来解决带约束的凸二次极大极小问题;提出了一种投影神经网络[42]来解决更一般的带约束的二次极大极小优化问题;提出了一种双时间尺度的神经动力学方法[43];协作神经动力学方法被用于多目标优化[44],[45]。
本文基于我们之前在神经动力学优化方面的工作,介绍了各种神经动力学方法来优化投资组合。将马科维茨投资组合选择问题重新表述为极大极小和双目标优化问题。在双层层次结构中,采用多神经动力学优化模型计算下层pareto最优解,采用粒子群优化算法优化上层pareto最优解的权重。使用四个主要的市场数据集来测试开发的方法在基于MV和平均条件风险值(CV aR)公式的极大极小和双目标问题中对最优投资组合的全局收敛性。
所提出的神经动力学方法在生物学上是合理的,并且具有并行分布和实时优化能力。与现有的固定权重问题公式[6]、[22]和仅优化SR的神经动力学方法[18]、[46]不同,本文开发了两种协同神经动力学方法来优化四种不同的目标函数和期望收益与风险之间的权重。因此,所提出的方法在公式合理性、解的最优性和实时可实现性方面具有优势。
本文的其余部分组织如下。
第二节介绍了投资组合优化的一些初步概念。第三节回顾了一些现有的神经动力学方法,用于极大极小和双目标优化。
第四节给出了用神经动力学方法求解极大极小和双目标投资组合问题的实验结果。第五节得出结论。
II. PROBLEM FORMULATIONS
在经典的Markowitz框架下,投资组合选择可以表述为基于MV及其变体均值-CVaR的极大极小和双准则优化问题。
A. MV 投资组合优化 与 SR
在本文中,我们做了如下假设[3],[21]:
1)所有资产都是无限可分的;
2)任何交易都可以即时执行;
3)与交易相关的成本和税收可以忽略不计。
设:
- n为投资组合的总资产数。
- u是投资组合平均收益的向量。
μ = ( μ 1 , μ 2 , . . . , μ n ) T μ = (μ_1, μ_2,... ,μ_n)^T μ=(μ1,μ2,...,μn)T
- y是投资财富占资产的比例。
y = ( y 1 , y 2 , . . . , y n ) T y = (y_1, y_2,... , y_n)^T y=(y1,y2,...,yn)T
- V为协方差矩阵。
- 投资组合的收益为 μ T y μ^Ty μTy
- 其方差为 y T V y y^TVy yTVy,衡量收益与均值的离散度。此外,回报率的标准差衡量波动性。
在实践中,方差和标准差都被用来衡量投资组合的风险。
MV框架旨在最小化风险或最大化投资组合的回报

其中 μ m i n μ_{min} μmin为投资组合收益的下界, σ m a x σ_{max} σmax为方差的上界,e为n维的单位向量, e T y e^T y eTy = 1为预算约束,且y的非负值(0 ~ 1之间)的限制表明不允许卖空。
在MV框架的基础上,以投资组合的收益与风险之比作为目标函数[46]-[48],提出了SR
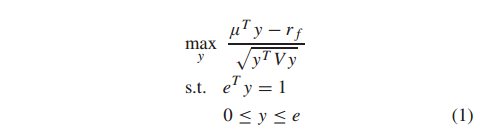
其中 r f r_f rf为无风险收益率。该比率将投资组合的超额收益(即 μ T y − r f μ^Ty − r_f μTy−rf )以标准差[49]进行标准化。SR值越高,表明持有风险较高的资产所带来的额外波动性带来的超额收益越大。没有超额收益的投资组合可能具有零SR值。然而,我们发现,在显著性水平小于0.9的情况下,最大化该比值有较高的概率会导致较大的损失[50]。
拓展:
显著性水平(Significance Level)是统计学中一个重要的概念;
通常用于评估研究结果的可靠性和统计显著性;
在假设检验中,显著性水平表示了对某个假设进行拒绝的临界值或阈值。
通常用α(alpha)来表示,它代表了犯第一类错误(错误地拒绝了一个正确的假设)的概率。
B. Conditional Value-at-Risk
MV框架的一个主要限制是方差不能衡量波动性的方向(即上行和下行风险)[16],[51]。
文献[6]提出了各种风险措施。其中,风险价值(VaR)是克服局限性的最常用的风险度量之一。
设 f l ( y , ξ ) f_l(y,ξ) fl(y,ξ)是一个关于 y y y的损失函数和一个随机向量 ξ ξ ξ, VaR定义为
V
a
R
=
m
i
n
{
ρ
∈
R
:
P
(
f
1
(
y
,
ξ
)
≤
ρ
)
≥
Θ
}
VaR = min\{ρ∈\mathbb{R}:\mathbb{P}(f_1(y,ξ)≤ρ)≥Θ\}
VaR=min{ρ∈R:P(f1(y,ξ)≤ρ)≥Θ}
其中$ 0 < θ < 1 $。
让我逐步解释这个公式👍:
- V a R VaR VaR:表示Value at Risk,也就是在给定的风险置信度下,可能的最大损失值。
- ρ ρ ρ:表示损失的金额,它是我们在寻找的VaR。
- P ( f 1 ( y , ξ ) ≤ ρ ) \mathbb{P}\left(f_1(y, ξ) ≤ ρ\right) P(f1(y,ξ)≤ρ):这是损失函数 f 1 ( y , ξ ) f_1(y, ξ) f1(y,ξ)小于等于 ρ ρ ρ的概率。也就是说,我们关心的是损失函数小于等于某个特定值的概率。
- Θ Θ Θ:是我们所设定的风险置信度,也就是我们希望的置信水平。例如,如果我们设定 Θ = 0.95 Θ = 0.95 Θ=0.95,那么我们希望在95%的情况下,损失不会超过 V a R VaR VaR。
所以,这个公式的意思是,在所有可能的损失值中,找到一个最小的 ρ ρ ρ,使得损失小于等于 ρ ρ ρ的概率大于等于我们设定的风险置信度 Θ Θ Θ。
然而,VaR具有非次可加性和非凸性等不良数学特性。
CVaR是在VaR基础上修正的一种一致性风险度量,定义为
C V a R = E { f l ( y , ξ ) ∣ f l ( y , ξ ) ≥ V a R } CVaR = \mathbb{E}\{f_l(y,ξ)|f_l(y,ξ)≥VaR\} CVaR=E{fl(y,ξ)∣fl(y,ξ)≥VaR}
其中 E ( ) \mathbb{E()} E() 是一种数学期望。
让我解释一下👍:
C V a R CVaR CVaR:表示 Conditional Value at Risk,也就是在给定 VaR 水平下的条件风险。
E { f l ( y , ξ ) ∣ f l ( y , ξ ) ≥ V a R } \mathbb{E}\{{f_l(y,ξ)|f_l(y,ξ)≥VaR}\} E{fl(y,ξ)∣fl(y,ξ)≥VaR}:这部分是一个条件期望(Conditional Expectation)的表达式。它表示在损失超过 VaR 的情况下,对损失函数 f l ( y , ξ ) f_l(y,ξ) fl(y,ξ) 进行期望。
具体来说,这个表达式的意思是,给定损失函数 f l ( y , ξ ) f_l(y,ξ) fl(y,ξ) 的取值超过 VaR 的情况,对这些超过 VaR 的情况下的损失值进行平均,这就得到了 CVaR。
这种表达方式强调了 CVaR 是在 VaR 水平之上的损失的平均值,而不考虑 VaR 以下的情况。因此,它提供了一个对高于 VaR 水平的风险的更为详细和全面的描述。
投资组合的CVaR可以用有限个的收益观测值 ξ 1 , ξ 2 , … ξ N ξ_1,ξ_2,…ξ_N ξ1,ξ2,…ξN (来计算)[15]
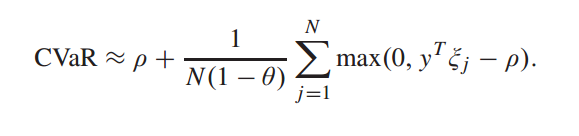
C. Minimax Portfolio Optimization
在实践中,投资者很难决定rf或σmax的值来实现他们的预期目标。因此,投资者自然会最大化最坏的预期回报(称为极大极小法)。将极大极小投资组合选择问题[21]表述为:
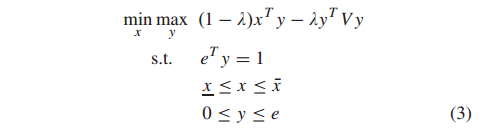
式中x = (x1, x2,…), xn)T为期望收益率,λ∈(0,1)为权值,x和x¯为x的下界和上界,分别为[55]。λ值越大,说明投资者的风险厌恶程度越高。投资者只在λ = 1时才考虑风险。相反,投资者是激进的,只在λ = 0时才考虑回报。请注意,方差可以用其他风险度量代替,例如(2)中的CVaR目标函数,对所有j具有约束zj≥yT ξ j−ρ
考虑一个一般的二次极大极小优化问题

这里的X、Y都是非空的封闭凸集
S和Q都是对称的半正定矩阵。
设φ(x, y)表示优化问题(4),x∧∈n, y∧∈n是两个非空紧凸集,f: x × y→∈一个实值函数,使得φ(x, y)对每一个固定的y在x上连续且凸,φ(x, y)对每一个固定的x在y上连续且凹。根据极大极小定理[56],存在一个鞍点(x∗,y∗)∈x × y,即
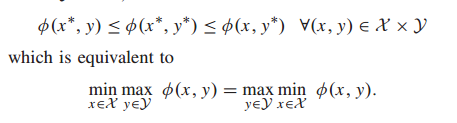
D. Biobjective Portfolio Optimization
投资组合优化问题也可以表述为一个双目标投资组合优化问题
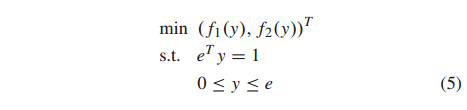
其中,f1(y)是投资组合风险度量,可以是方差或CVaR, f2(y)是投资组合预期收益的负值。将CVaR作为优化问题(5)的目标函数,对所有j的约束条件为 z j ≥ y T ξ j − ρ z_j≥y^Tξ_j−ρ zj≥yTξj−ρ,建立了一个多目标线性规划问题。
由于投资组合优化问题包含两个目标,因此通过优化问题可以找到一个最优投资组合集合,该集合由可行集中所有不受其他组合支配的可行投资组合组成。
考虑到两个解y’以及y’‘。如果y’‘的两个目标都大于y’的值,则成为y‘’支配y’
帕累托最优解y*:不存在支配于它的解。
由于目标函数相互冲突,双目标优化问题不存在单一的最优解,这时候的解就是Pareto optimal解。
标量化是一种流行的方法,可用于解决(5)[22],[23]。它提出了一个具有预定义权重的标化优化问题(单目标)

鉴于(6)是非光滑的,可以将其重新表述为约束优化问题。让ζ= max{λ(f1 (y)−f∗1),(1−λ)(f2 (y)−f∗2)}。(6)中的优化问题重新表述为
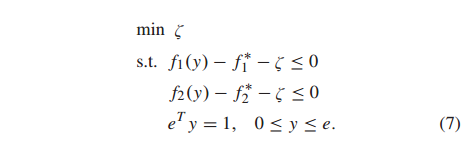
这是一个约束凸优化问题。如果使用CVaR作为风险函数,则需要在(7)中添加对所有j的约束 z j ≥ y T ξ j − ρ z_j≥y^T ξ_j−ρ zj≥yTξj−ρ
极大极小和双目标投资组合公式都是基于风险和回报。然而,双目标公式对投资者的风险行为是敏感的,而极大极小组合公式对投资者的风险行为是稳健的,这在第四节的计算结果中得到了证明。
III. NEURODYNAMIC OPTIMIZATION
A. Neurodynamic Approach to Biobjective Optimization
-
为了使(3)具有分布良好的非支配解的Pareto最优性和多样性,在双层层次结构中使用了一种带有权重优化的多目标优化协同神经动力学方法[45]。
-
为了达到最优性,多个神经网络并行使用,通过在底层通过加权切比雪夫标量化最小化一个标化的目标函数来生成一组帕累托最优解。
-
为了通过分布良好的解决方案实现多样性,预期收益和风险之间的权重根据更高级别的性能度量(即最大化hypervolume)进行优化。
-
PS:
-
非支配解其定义为:假设任何二解
S1及S2对所有目标而言,S1均优于S2,则我们称S1支配S2,若S1的解没有被其他解所支配,则S1称为非支配解。 -
切比雪夫标量化是一种常用的数据预处理方法,它可以将数据映射到一个特定的区间,以便更好地进行数据分析和建模。切比雪夫标量化的目标是通过对数据进行线性变换,使得数据在某个区间内分布均匀,并尽可能地保持数据的原始相对位置关系。
如图1所示,hypervolume和权重之间的关系不能用函数表示。
因此,使用元启发式优化算法(即PSO[59])来最大化相对于权重{λ1,…,λM},因为不需要目标函数[60],[61]。基于神经动力学的Parento解搜索和基于pso的权重优化交替进行,以实现解的最优性和多样性。
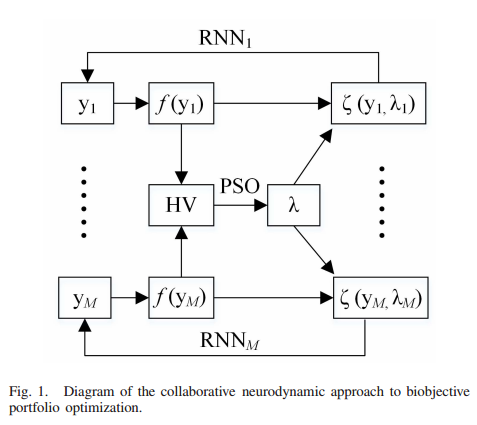
图1:双目标投资组合优化的协同神经动力学方法示意图
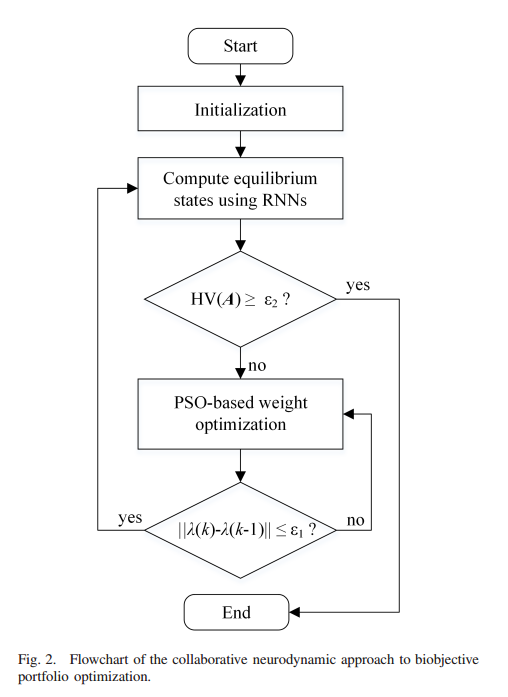
图2显示了该方法的流程图:用粒子群算法更新权值,直到收敛(即用λ(k)−λ(k−1)或超体积值大于阈值(即, H V ( A ) ≥ ε 2 HV(A)≥ε_2 HV(A)≥ε2,其中A为最佳组合的集合, ε 2 ε_2 ε2为阈值)为止。
许多全局收敛的神经动力学模型(见[30],[31],[62]-[65])可用于标化后的双目标优化。
以双目标投资组合优化为例(7),神经动力学优化模型[64]的动力学方程定义如下:
{
ϵ
d
η
d
t
=
−
η
+
P
Ω
[
η
−
e
n
+
1
−
∇
g
(
η
)
δ
−
∇
h
(
η
)
γ
]
ϵ
d
δ
d
t
=
−
δ
+
[
δ
+
g
(
η
)
]
+
ϵ
d
γ
d
t
=
−
h
(
η
)
\left\{\begin{array}{l} \epsilon \frac{d \eta}{d t}=-\eta+P_{\Omega}\left[\eta-e_{n+1}-\nabla g(\eta) \delta-\nabla h(\eta) \gamma\right] \\ \epsilon \frac{d \delta}{d t}=-\delta+[\delta+g(\eta)]^{+} \\ \epsilon \frac{d \gamma}{d t}=-h(\eta) \end{array}\right.
⎩
⎨
⎧ϵdtdη=−η+PΩ[η−en+1−∇g(η)δ−∇h(η)γ]ϵdtdδ=−δ+[δ+g(η)]+ϵdtdγ=−h(η)
(8)式中
R是德文尖角体(fraktur),\mathfrak{}
- ε ε ε为正时间常数(读音:epsilon)
- η = ( y T , ζ ) T ∈ R n + 1 η= (y^T,ζ)^T∈\mathfrak{R}^{n+1} η=(yT,ζ)T∈Rn+1为状态向量(读音:伊塔)
- δ ∈ R 2 , γ ∈ R δ∈\mathfrak{R}^2,γ∈\mathfrak{R} δ∈R2,γ∈R为隐藏状态向量和变量。
- e n + 1 = ( 0 , 0 , … ,, 0 , 1 ) T ∈ R n + 1 e_{n+1} =(0,0,…,, 0,1)^T∈\mathfrak{R}^{n+1} en+1=(0,0,…,,0,1)T∈Rn+1,
- g ( η ) = ( f 1 ( y ) − f 1 ∗ − ζ , f 2 ( y ) − f 2 ∗ − ζ ) T g(η) = (f_1(y)−f^∗_1−ζ, f_2(y)−f^∗_2−ζ)^T g(η)=(f1(y)−f1∗−ζ,f2(y)−f2∗−ζ)T
- h ( η ) = e T y − 1 h(η) = e^T y−1 h(η)=eTy−1
- 且 P Ω ( ⋅ ) P_Ω(·) PΩ(⋅)是分段线性激活函数,定义为
P Ω ( v i ) = { v ˉ i , v i > v ˉ i v i , v ‾ i ≤ v i ≤ v ~ i v ‾ i , v i < v ‾ i ( 9 ) P_{\Omega}(v_i)=\begin{cases}\bar{v}_i,&v_i>\bar{v}_i\\v_i,&\underline{v}_i\leq v_i\leq\tilde{v}_i\\\underline{v}_i,&v_i<\underline{v}_i\end{cases}\quad(9) PΩ(vi)=⎩ ⎨ ⎧vˉi,vi,vi,vi>vˉivi≤vi≤v~ivi<vi(9)
其中 v ‾ i \underline{v}_i vi和 v ˉ i \bar{v}_i vˉi分别为v的下界和上界, [ η ] + = m a x { η , 0 } [η]+=max\{{η, 0\}} [η]+=max{η,0}是另一个分段线性(ReLu)激活函数,其中 v = 0 v = 0 v=0, v ˉ = e \bar{v}=e vˉ=e。
PS:这个公式描述了一个用于双目标投资组合优化的神经动力学模型。让我们逐步解释每个部分:
-
ϵ d η d t = − η + P Ω [ η − e n + 1 − ∇ g ( η ) δ − ∇ h ( η ) γ ] \epsilon \frac{d \eta}{d t}=-\eta+P_{\Omega}\left[\eta-e_{n+1}-\nabla g(\eta) \delta-\nabla h(\eta) \gamma\right] ϵdtdη=−η+PΩ[η−en+1−∇g(η)δ−∇h(η)γ]
- η \eta η 是一个表示投资组合的向量,它的动态变化受时间的影响。
- ϵ d η d t \epsilon \frac{d \eta}{d t} ϵdtdη 表示随时间变化的 η \eta η 的变化率, ϵ \epsilon ϵ 是一个正常数,可能用来调整变化的速率。
- P Ω P_{\Omega} PΩ 可能表示投影算子,用来确保 η \eta η 始终保持在某个特定的约束集合 Ω \Omega Ω 中。
- η − e n + 1 − ∇ g ( η ) δ − ∇ h ( η ) γ \eta-e_{n+1}-\nabla g(\eta) \delta-\nabla h(\eta) \gamma η−en+1−∇g(η)δ−∇h(η)γ 是一个关于 η \eta η、 δ \delta δ 和 γ \gamma γ 的复杂表达式。
这个方程描述了 η \eta η 随时间变化的规律,右侧的表达式包含了关于当前投资组合 η \eta η、目标 δ \delta δ 和 γ \gamma γ 以及函数 g g g 和 h h h 的信息。
-
ϵ d δ d t = − δ + [ δ + g ( η ) ] + \epsilon \frac{d \delta}{d t}=-\delta+[\delta+g(\eta)]^{+} ϵdtdδ=−δ+[δ+g(η)]+
- δ \delta δ 也是一个表示投资组合的向量,它的动态变化也受时间的影响。
- [ δ + g ( η ) ] + [\delta+g(\eta)]^{+} [δ+g(η)]+ 表示将 δ + g ( η ) \delta+g(\eta) δ+g(η) 的正部分(即大于零的部分)保留,小于零的部分置零。
- ϵ d δ d t \epsilon \frac{d \delta}{d t} ϵdtdδ 表示随时间变化的 δ \delta δ 的变化率,同样, ϵ \epsilon ϵ 是一个正常数。
这个方程描述了 δ \delta δ 随时间变化的规律,右侧的表达式包含了关于当前投资组合 η \eta η 和函数 g g g 的信息。
-
ϵ d γ d t = − h ( η ) \epsilon \frac{d \gamma}{d t}=-h(\eta) ϵdtdγ=−h(η)
- γ \gamma γ 是另一个表示投资组合的向量,它的动态变化也受时间的影响。
- ϵ d γ d t \epsilon \frac{d \gamma}{d t} ϵdtdγ 表示随时间变化的 γ \gamma γ 的变化率,同样, ϵ \epsilon ϵ 是一个正常数。
- h ( η ) h(\eta) h(η) 是一个关于 η \eta η 的函数。
这个方程描述了 γ \gamma γ 随时间变化的规律,右侧的表达式包含了关于当前投资组合 η \eta η 和函数 h h h 的信息。
总的来说,这组方程描述了一个动态系统,其中投资组合的三个部分 η \eta η、 δ \delta δ 和 γ \gamma γ 都随时间变化。系统的动态变化受到目标函数 g g g 和 h h h 的影响,同时受到约束条件以及投影算子的限制。这种动态系统的模型可以用于双目标投资组合优化问题。
B. Neurodynamic Approaches to Minimax Optimization
几种神经动力学模型可用于极大极小优化[41]-[43]。例如,[41]中求解(4)的投影神经网络模型定义如下:
{
ϵ
d
x
d
t
=
−
(
x
−
P
X
[
x
−
α
(
S
x
+
s
−
H
y
)
]
)
ϵ
d
y
d
t
=
−
(
y
−
P
Y
[
y
−
α
(
Q
y
+
q
+
H
T
x
)
]
)
.
\left\{\begin{array}{l} \epsilon \frac{d x}{d t}=-\left(x-P_{\mathcal{X}}[x-\alpha(S x+s-H y)]\right) \\ \epsilon \frac{d y}{d t}=-\left(y-P_{\mathcal{Y}}\left[y-\alpha\left(Q y+q+H^T x\right)\right]\right) . \end{array}\right.
{ϵdtdx=−(x−PX[x−α(Sx+s−Hy)])ϵdtdy=−(y−PY[y−α(Qy+q+HTx)]).
(公式10)
如果满足其中一个充分条件,则证明了它是 Lyapunov stable (稳定)
为了降低模型复杂度和解决更普遍约束的二次极大极小优化问题,在[42]中提出了一个投影神经网络,其状态方程如下:
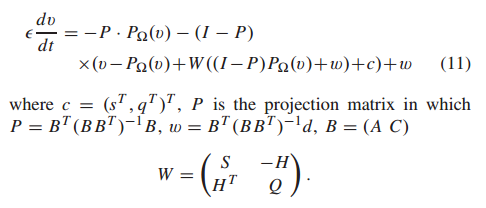
神经动力学模型(11)被证明是全局稳定的,并收敛于(4)[42]的最优解。
为了解决一般的凸凹极小极大优化问题,提出了一个双时间尺度神经动力学框架[43],该框架也可用于解决(4)等问题。该方法由两个不同时间尺度的耦合递归神经网络组成:一个用于目标函数的最小化,另一个用于目标函数的最大化。这个动力方程的一般形式如下:
{
ϵ
1
d
x
d
t
∈
F
(
∂
ϕ
(
x
,
y
)
,
X
)
ϵ
2
d
y
d
t
∈
F
(
−
∂
ϕ
(
x
,
y
)
,
Y
)
\begin{cases}\epsilon_1\dfrac{dx}{dt}\in F(\partial\phi(x,y),\mathcal{X})\\[2ex]\epsilon_2\dfrac{dy}{dt}\in F(-\partial\phi(x,y),\mathcal{Y})\end{cases}
⎩
⎨
⎧ϵ1dtdx∈F(∂ϕ(x,y),X)ϵ2dtdy∈F(−∂ϕ(x,y),Y)
其中
F
(
⋅
)
F(·)
F(⋅)是
∂
φ
(
x
,
y
)
∂φ(x, y)
∂φ(x,y)与
x
x
x或
y
y
y的函数,
∂
φ
(
x
,
y
)
∂φ(x, y)
∂φ(x,y)是
φ
(
x
,
y
)
φ(x, y)
φ(x,y)的Clarke广义梯度[66],φ(x, y)不一定是二次的。请注意,ζ1和ζ2是两个不同的时间常数,因此两个神经网络具有不同的收敛速率。[43]表明,双时间尺度神经动力学方法收敛于极大极小优化问题的最优解。
与双目标投资组合优化的神经动力学方法类似,在双层层次结构中开发了一种解决极大极小投资组合优化问题的协作神经动力学方法(3),并通过使用多个神经动力学优化模型(11)(解决方案最优性)和PSO(解决方案多样性)来产生分布良好的有效前沿。
PS:
广义梯度(generalized gradient)是梯度或导数概念的一种推广,这是克拉克(Clarke,F.H.)对于局部李普希茨函数类提出的概念,由此形成的理论已成为非光滑分析中最成熟的一部分,并且有广泛的应用。
广义梯度是对梯度的一种推广,它可以用来描述任意维度的函数。
广义梯度的定义是:对于一个函数f(x),它的广义梯度是一个向量值函数,它的每个分量都是f(x)在相应坐标轴上的偏导数。也就是说,广义梯度是一个向量,它的每个分量都是函数在相应坐标轴上的变化率。
该框架由两个递归神经网络组成,一个用于最小化目标函数,另一个用于最大化目标函数。该方法的核心在于使用两个不同时间尺度的神经网络来处理优化问题,其中较小时间尺度的网络用于调整权重和偏差,较大时间尺度的网络则用于更新权重和偏差。
在具体实现上,该方法使用了Clarke广义梯度来计算目标函数的梯度,因此能够处理非二次目标函数。此外,由于使用了不同的时间常数,两个神经网络具有不同的收敛速率,从而能够更好地处理不同时间尺度的优化问题。
最后,该段内容提到了类似的方法也被应用于解决极大极小投资组合优化问题。通过使用多个神经动力学优化模型和粒子群优化(PSO)来产生分布良好的有效前沿,从而得到更好的解决方案。
IV. COMPUTATIONAL RESULTS(实验部分)
本节分为三个部分。
-
第IV-A节介绍了从真实市场数据构建的四个数据集。
-
第IV-B节介绍了基于MV和mean- cvar公式的极大极小和双目标投资组合优化问题的状态向量和目标函数的瞬态行为,使用应用的神经动力学模型,使用权重优化的权重和平均超体积值的变化,以及生成的有效边界。对于投资组合选择问题,神经动力学模型的数量和权重设置为20。
-
第IV-C节讨论了与其他投资组合策略进行极大极小和双目标投资组合优化的比较结果
注意:千万不要被大量的图给劝退了,这里的实验主要是控制变量后组合排列形成的实验。
A. Test Data Sets
基于HDAX、FTSE、HSI和SP500四个全球知名股票市场构建了四个数据集。
HDAX(德国交易所DAX100的继承者)数据集包括DAX(30家主要公司),MDAX(50家主要标准股票)和TecDAX(30家最大的科技公司)的股票信息。
FTSE富时指数公司数据集由伦敦证券交易所市值最高的100只股票信息组成。
富时指数公司(Financial Times and Stock Exchange)
HSI恒生指数的数据集包括香港交易所恒生综合大型股指数和恒生综合中型股指数的股票信息。
恒生指数(Hang Seng Index)
标准普尔500指数数据集包括在纽约证券交易所和纳斯达克股票市场上市的500家大型公司的普通股。数据为雅虎财经2000年1月1日至2018年1月1日每周调整后的收盘价。根据惯例[67]-[69],期间内的停牌和新上市股票被排除在外。因此,测试数据
从HDAX、FTSE、HSI和SP500数据库中提取的数据集包含48、58、90和384只股票的信息;
B. Simulation Results
在极大极小和双目标组合优化问题中,当权重设置为0.5时,描述了神经网络状态向量的瞬态行为,并对状态向量进行了表征。从图3和图4可以看出,神经动力学模型(11)在求解各种数据集的极大极小组合优化问题(3)时是收敛的。每个子图都表明状态向量y收敛于向量x对每个数据集的最差预期收益下的最优资产配置。通过对比图3和图4可以看出,基于MV和均值-cvar公式,每个数据集的资产配置略有不同。
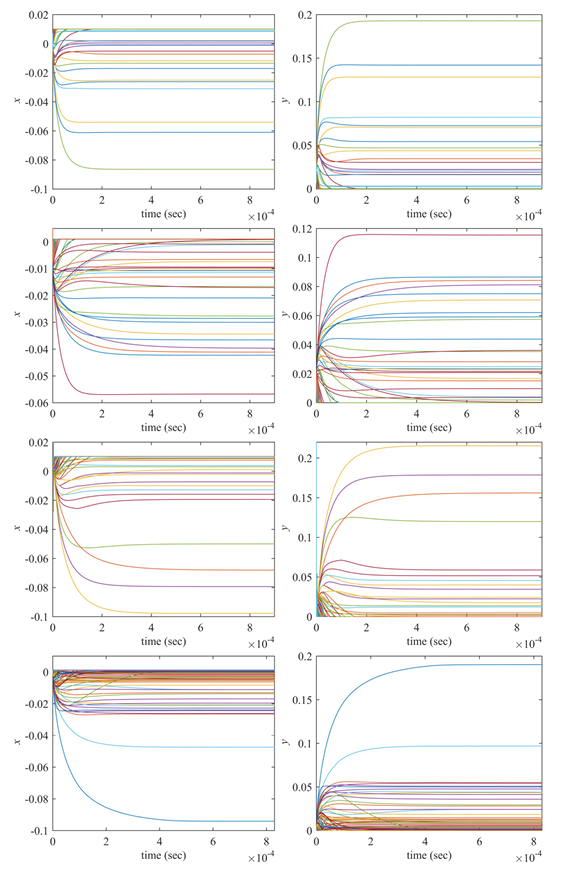
Fig3:基于HDAX(第一行子图)、FTSE(第二行子图)、HSI(第三行子图)和SP500(最后一行子图)数据集的MV公式求解极大极小投资组合优化问题(3)的神经动力学模型(11)中的瞬态x和y。
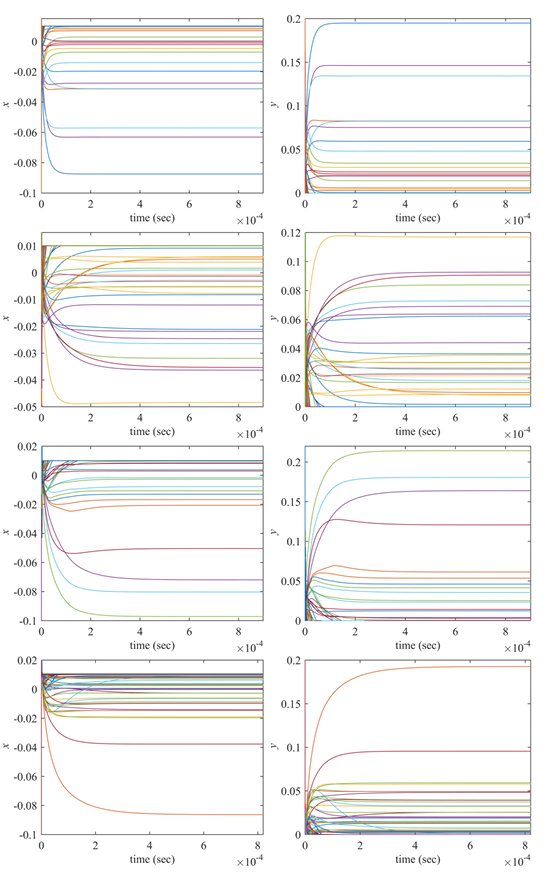
Fig 4:以HDAX(第一行子图)、FTSE(第二行子图)、HSI(第三行子图)和SP500(最后一行子图)为数据集,基于均值-cvar公式的最小化投资组合优化问题(3)中神经动力学模型(11)的瞬态x和y。
图5和图6显示了问题(3)中基于粒子群算法的权重优化在不同数据集下λ的变化。可以看出,权重在20次迭代内收敛。
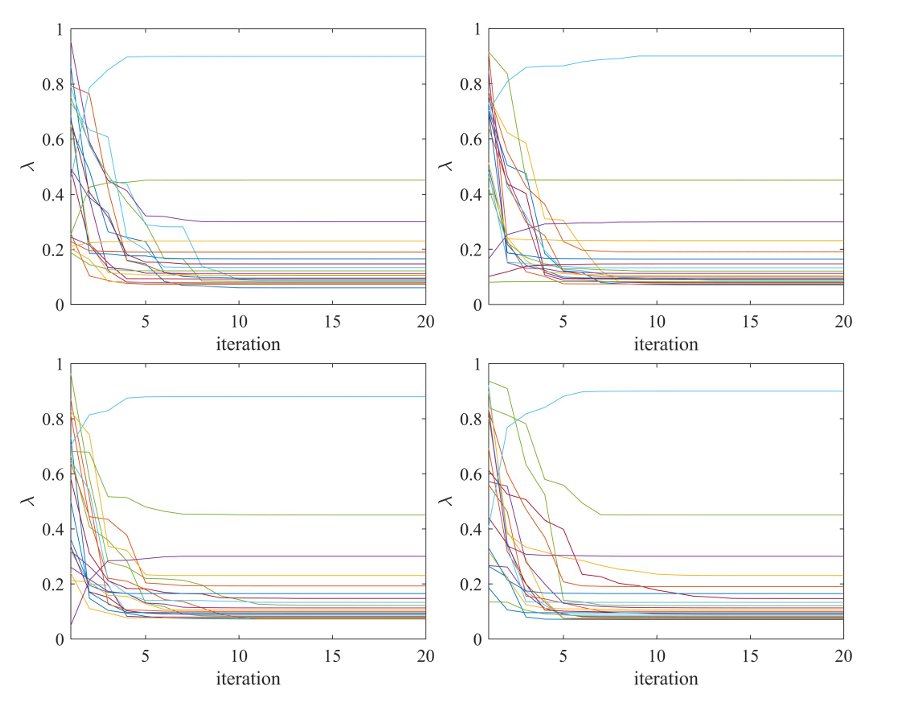
Fig 5:HDAX(左上子图)、FTSE(右上子图)、HSI(左下子图)、SP500(右下子图)数据集基于MV公式的极大极小投资组合优化问题(3)中基于pso的权重优化过程。
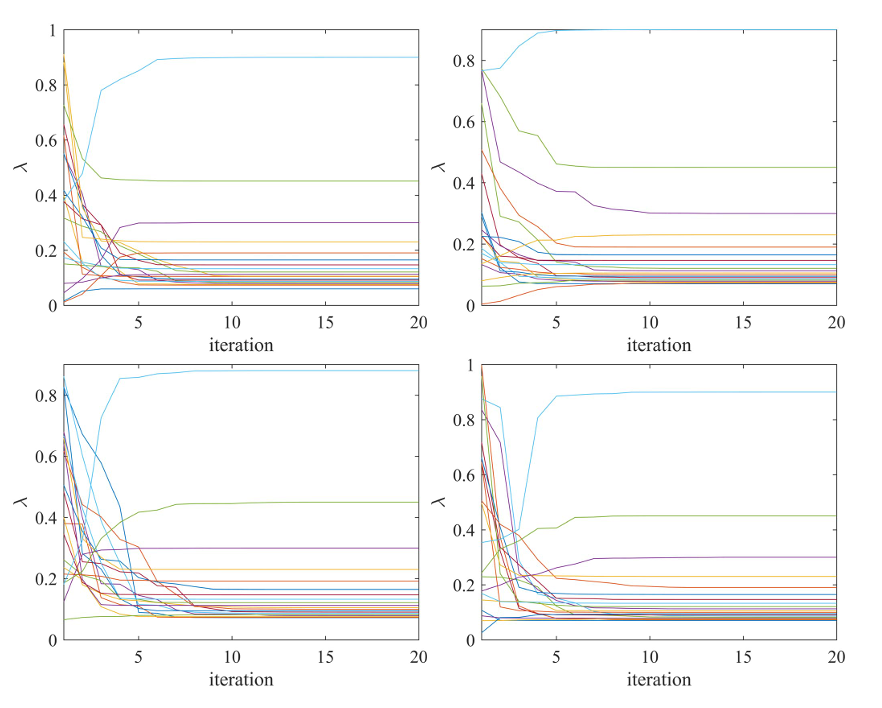
Fig 6 :基于均值-CVaR公式,HDAX(左上子图)、FTSE(右上子图)、HSI(左下子图)和SP500(右下子图)数据集的最小化投资组合优化问题(3)中基于pso的权重优化过程。
图7和图8显示了问题(3)中目标函数值在不同权重下的瞬态行为。
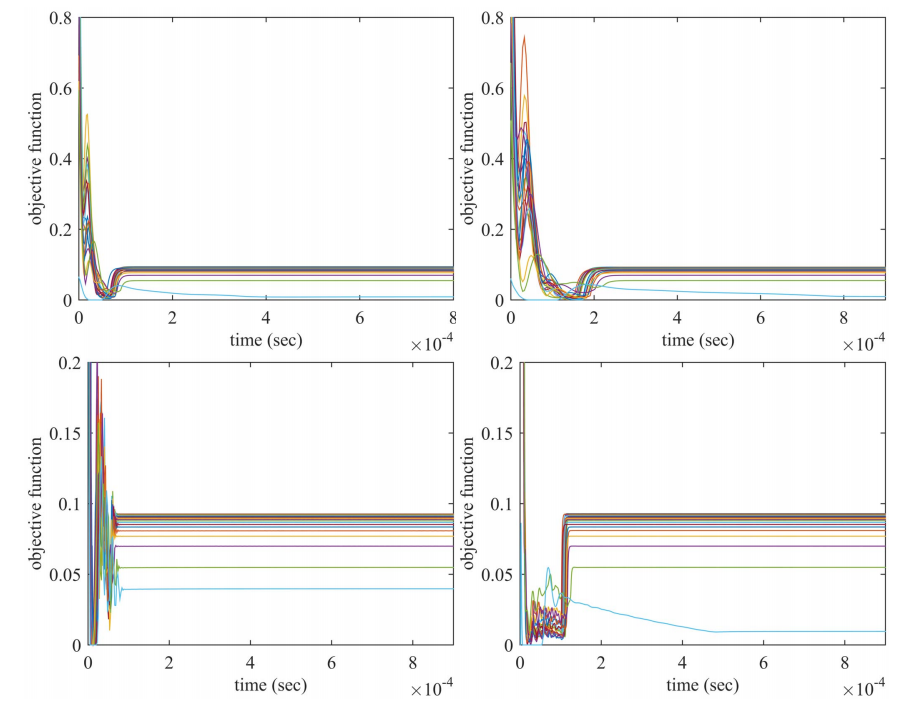
Fig.7. 基于MV公式的HDAX(左上子图)、FTSE(右上子图)、HSI(左下子图)和SP500(右下子图)数据集的极大极小投资组合优化问题(3)中目标函数值的瞬态行为
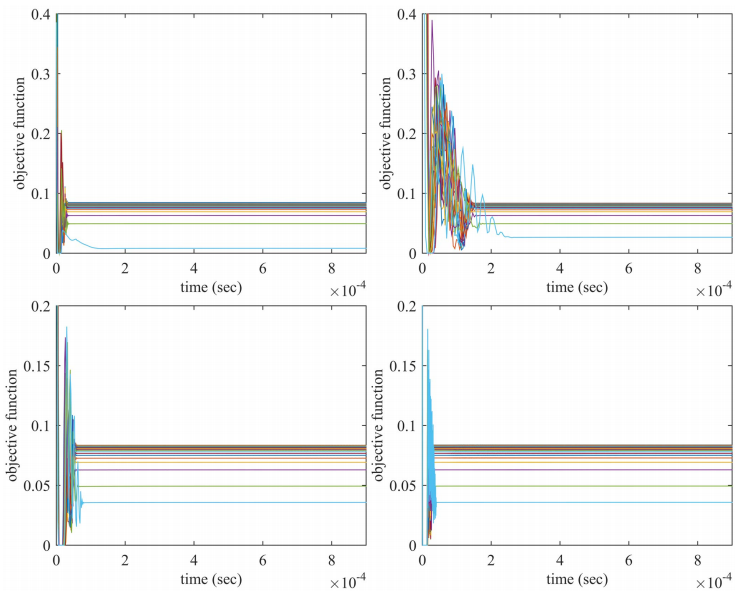
Fig.8. 利用HDAX(左上子图)、FTSE(右上子图)、HSI(左下子图)和SP500(右下子图)数据集,基于均值-CVaR公式的极大极小投资组合优化问题(3)中目标函数值的瞬态行为。
从图9和图10可以看出,神经动力学模型(8)在用数据集求解问题(7)时是收敛的,从子图可以看出状态向量y收敛于各种最优资产配置。
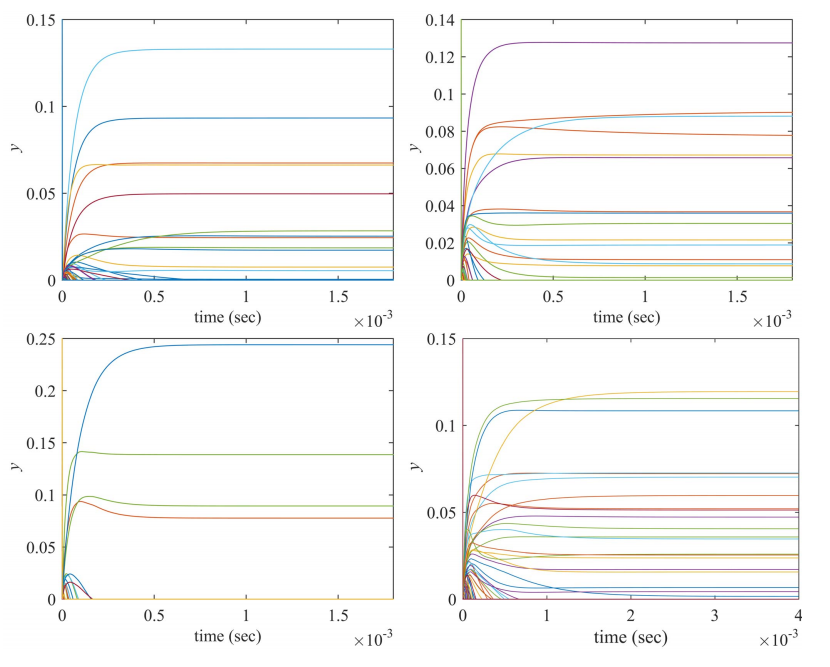
Fig.9. 基于MV公式的HDAX(左上子图)、FTSE(右上子图)、HSI(左下子图)和SP500(右下子图)数据集的双目标投资组合优化问题(7)中神经动力学模型(8)的瞬态y。
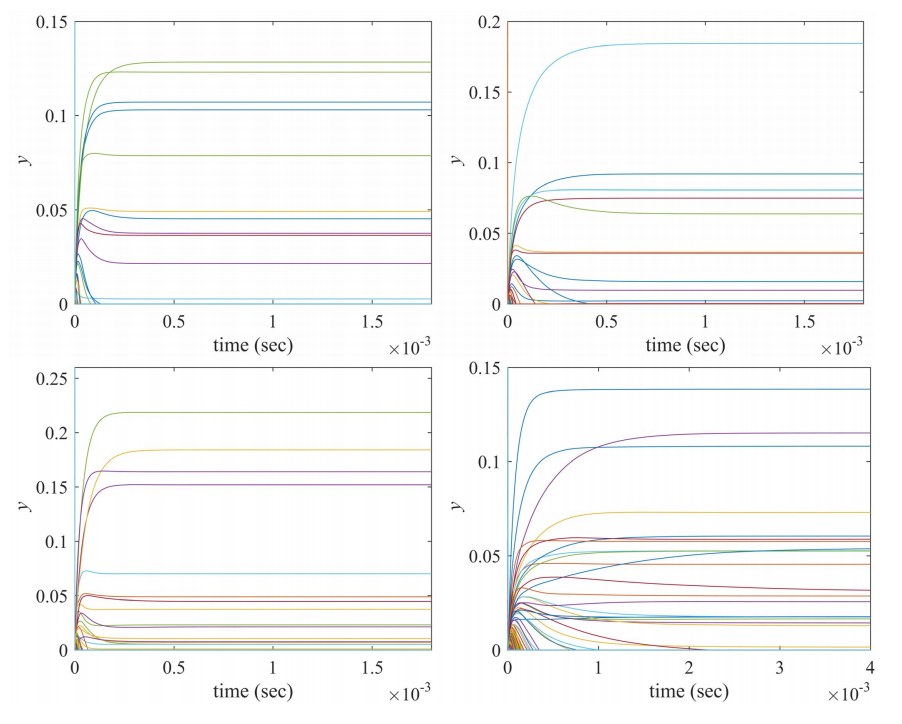
Fig.10. 基于均值- cvar公式的HDAX(左上子图)、FTSE(右上子图)、HSI(左下子图)和SP500(右下子图)数据集的双目标投资组合优化问题(7)中神经动力学模型(8)的瞬态y
图11和图12显示了优化问题(7)的目标函数值在数据集下的瞬态行为。
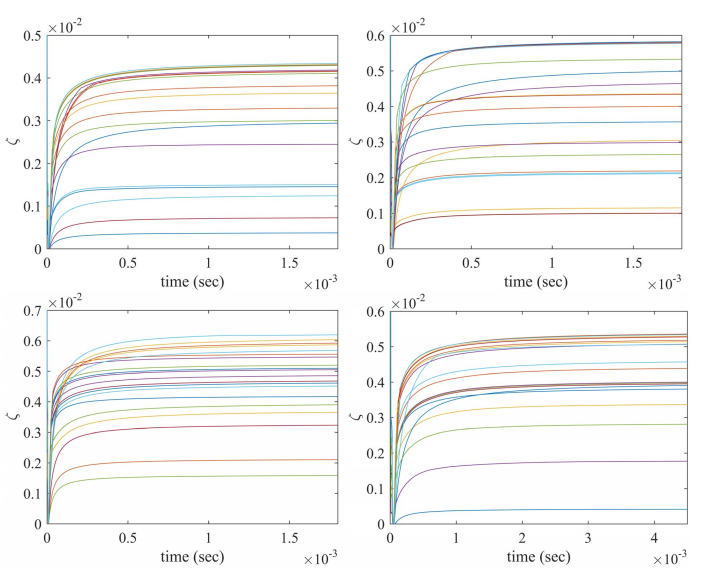
Fig.11. 基于MV公式的HDAX(左上子图)、FTSE(右上子图)、HSI(左下子图)和SP500(右下子图)数据集的双目标投资组合优化问题(7)中标化目标函数值的瞬态行为
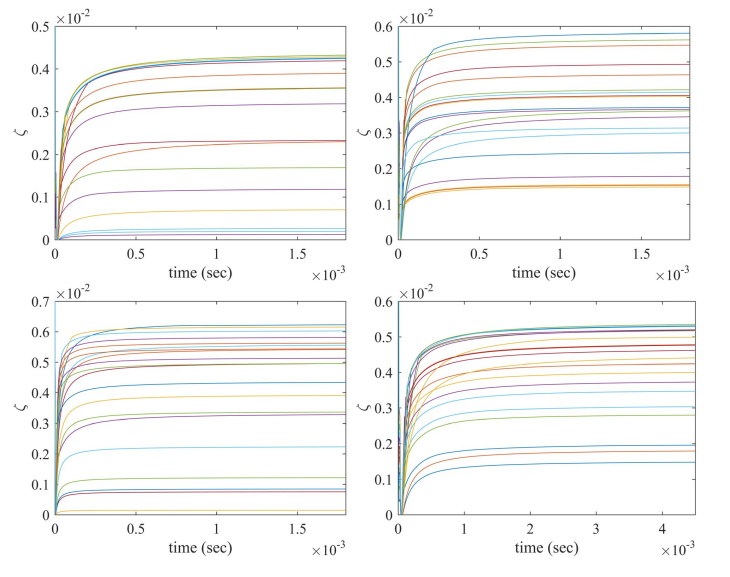
Fig.12. 基于均值- cvar公式的HDAX(左上子图)、FTSE(右上子图)、HSI(左下子图)和SP500(右下子图)数据集的双目标投资组合优化问题(7)中标化目标函数值的瞬态行为。
图13和图14分别显示了基于pso的权重优化在问题(7)中基于MV和mean-CVaR公式的λ变化。
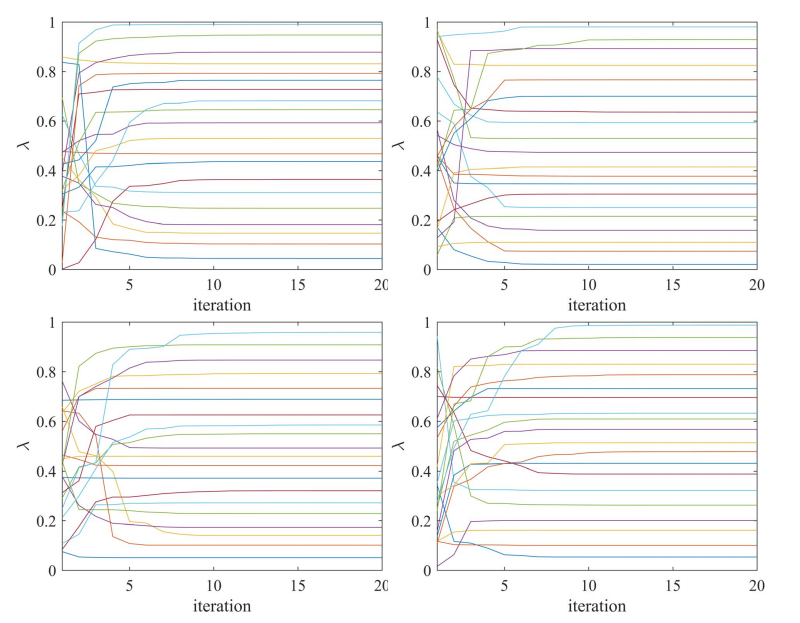
Fig.13. 基于MV公式的HDAX(左上子图)、FTSE(右上子图)、HSI(左下子图)和SP500(右下子图)数据集的双目标投资组合优化问题(7)中基于pso的权重优化过程。
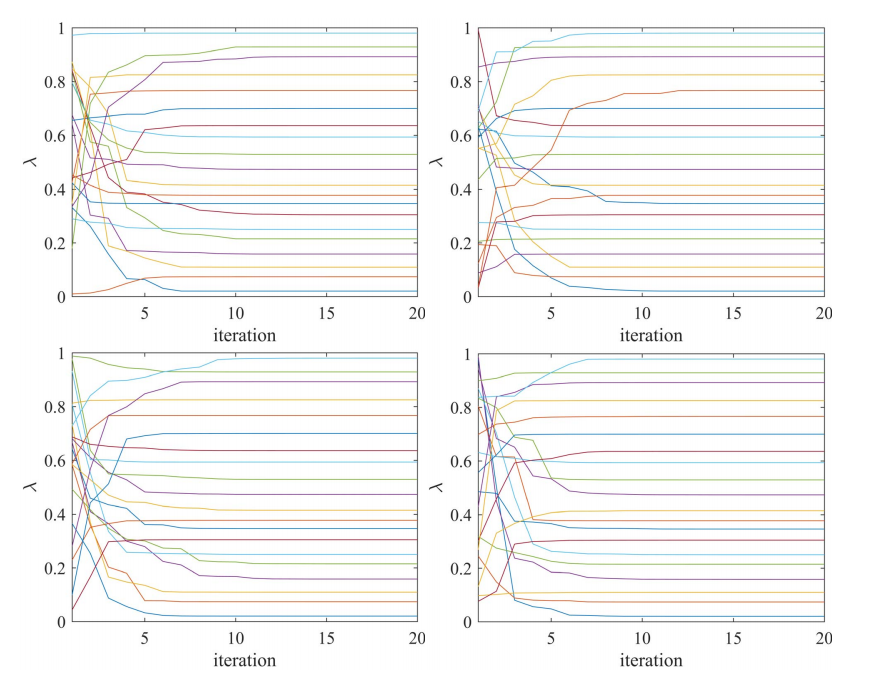
Fig.14. 基于均值- cvar公式的双目标投资组合优化问题(7)中基于pso的权重优化过程,HDAX(左上子图)、FTSE(右上子图)、HSI(左下子图)和SP500(右下子图)数据集。
图15显示了基于pso的权重优化对极大极小和双目标投资组合优化问题基于其MV和均值cvar公式的平均超容积值hypervolume的变化,其中MMMV和MMMC分别表示基于MV和均值cvar公式的最优极大极小投资组合,BOMV和BOMC分别表示基于MV和均值cvar公式的最优双目标投资组合。可以看出BOMC总是获得最大的超卷值,而BOMV总是获得最小的超卷值。
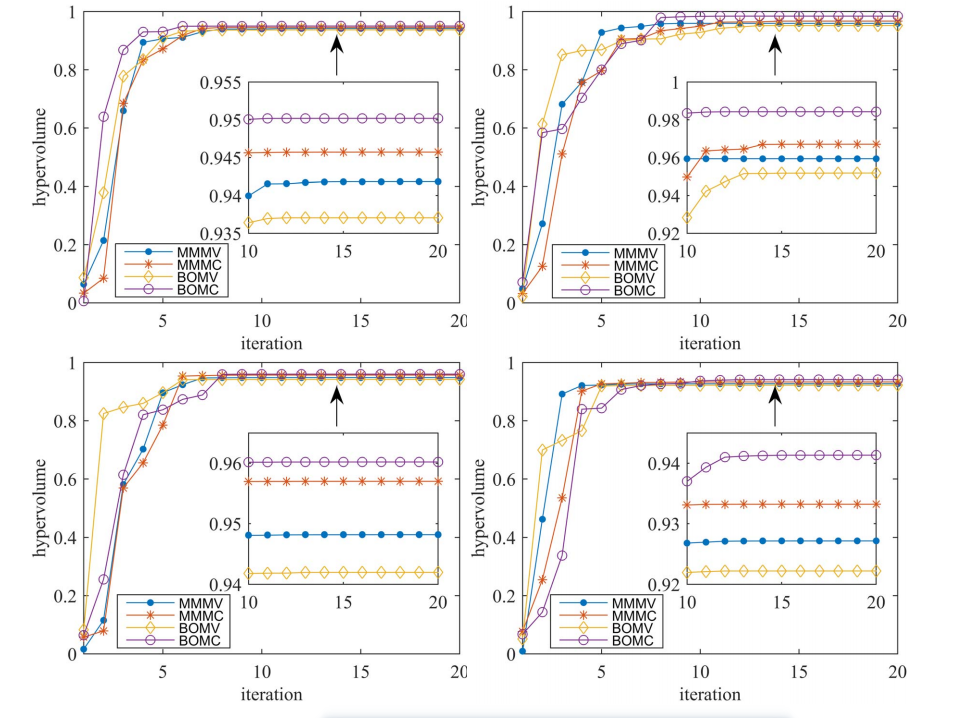
Fig.15. 基于MV和Mean - cvar公式的最小化和双目标投资组合优化问题中基于pso的权重优化中的平均超容积值,数据集为HDAX(左上子图)、FTSE(右上子图)、HSI(左下子图)和SP500(右下子图)。
此外,在50次独立运行的双目标均值- cvar组合优化中,将粒子群优化算法与差分进化(DE)[70]、蚁群优化(ACO)[71]、遗传算法(GA)[72]等元启发式算法的权重优化性能进行了比较。
每个算法的人口大小设置为20。所有算法在第20次迭代时终止。图16记录了通过比较算法得到的解的hypervolume值。图16还显示了PSO在四个数据集上的收敛速度比其他算法快。
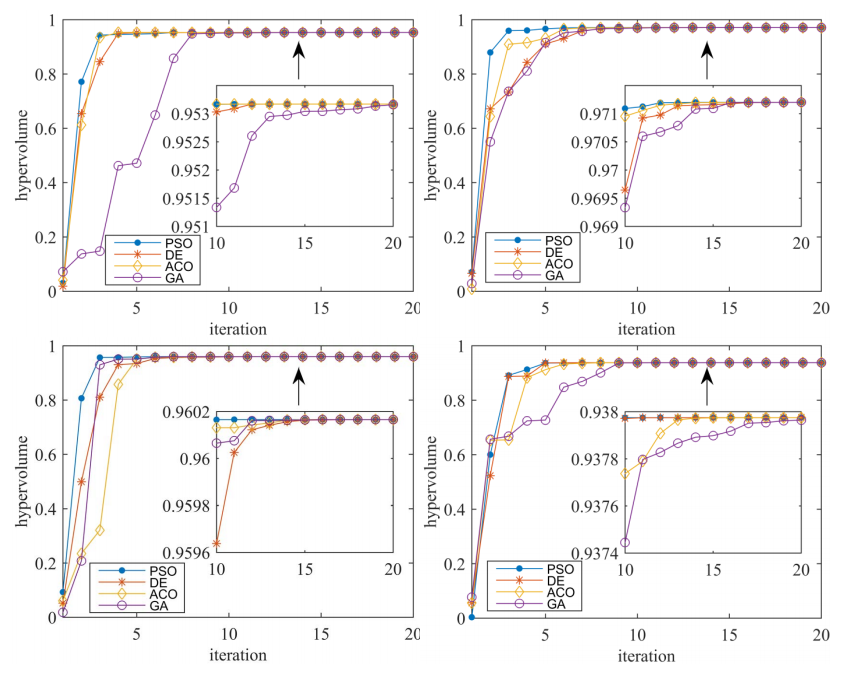
Fig.16. 基于HDAX(左上子图)、FTSE(右上子图)、HSI(左下子图)和SP500(右下子图)数据集的均值- cvar公式的双目标投资组合优化中迭代的平均超容量值。
图17显示了使用神经动力学方法通过极大极小和双目标组合优化问题获得的组合回报。可以看出,考虑到投资组合收益和波动率,双目标解的范围比极大极小解的范围更大。
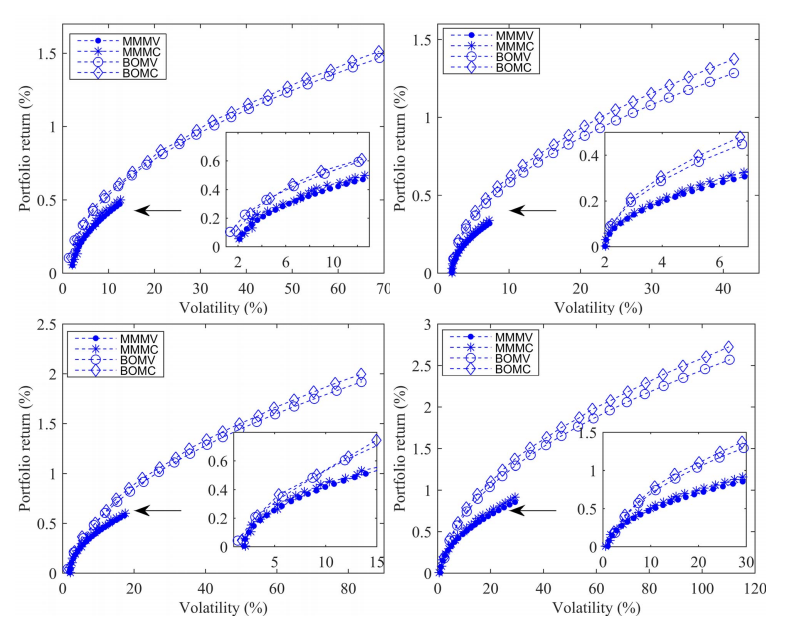
Fig.17. 通过基于MV和mean-CVaR公式的极大极小和双目标投资组合优化问题获得的PFs,数据集为HDAX(左上子图)、FTSE(右上子图)、HSI(左下子图)和SP500(右下子图)。
图17清楚地表明,双目标方法对λ很敏感,而极大极小方法则更加稳健。
C. Comparative Studies
样本内和样本外检验是根据数据集中股票的历史收益进行的
表1记录了基于数据集的不同投资组合的年化收益,其中MI表示市场指数(在数据序列开始时归一化为1),EW表示在实践中广泛使用的等权重投资组合[73],[74],
SR表示利用投影神经网络[46]实现SR最大化(1)的最优投资组合。最小最大值和双目标投资组合的平均值(圆括号内为标准差)和范围也被记录下来
Table1 : 来自于不同的投资组合年化收益
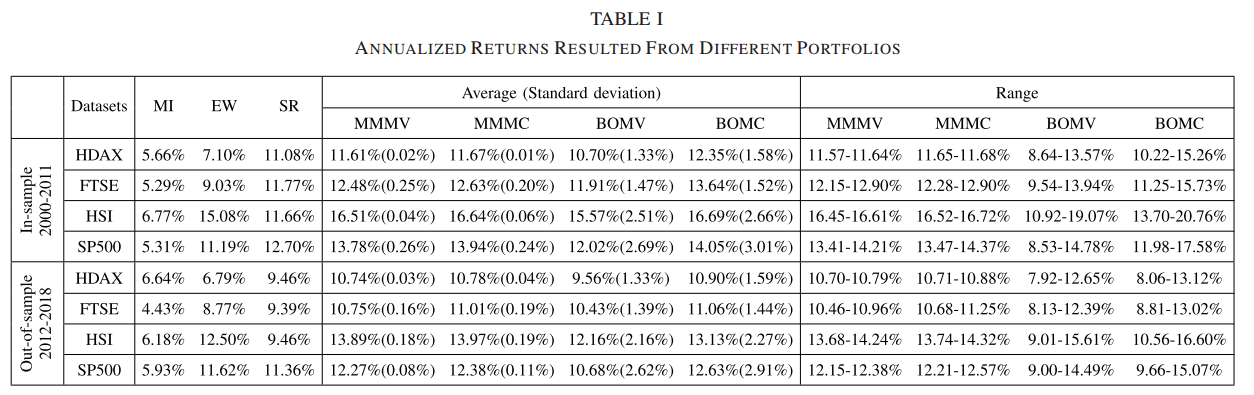
根据表1的结果可以发现一些观察结果。对于忽略市场指数的每个投资组合,样本内检验的表现通常优于样本外检验,这是不适用的。
此外,基于均值- cvar公式的投资组合选择优于基于MV的投资组合选择,减轻了波动率测量方向的限制,并且双目标均值- cvar (BOMC)公式可以在每个数据集上产生最高的年化收益。此外,应该注意的是,MMMC和MMMV的年化收益率范围较小,而BOMC和BOMV的年化收益率范围在样本内和样本外检验中都要大得多。一方面,保守型投资者适合选择年化收益更稳定的极大极小投资组合。另一方面,激进的投资者可以选择双目标投资组合,如果使用适当的权重,可以带来更高的回报。
图18显示了基于四个数据集的不同投资组合在2000 - 2018年的累计对数收益。
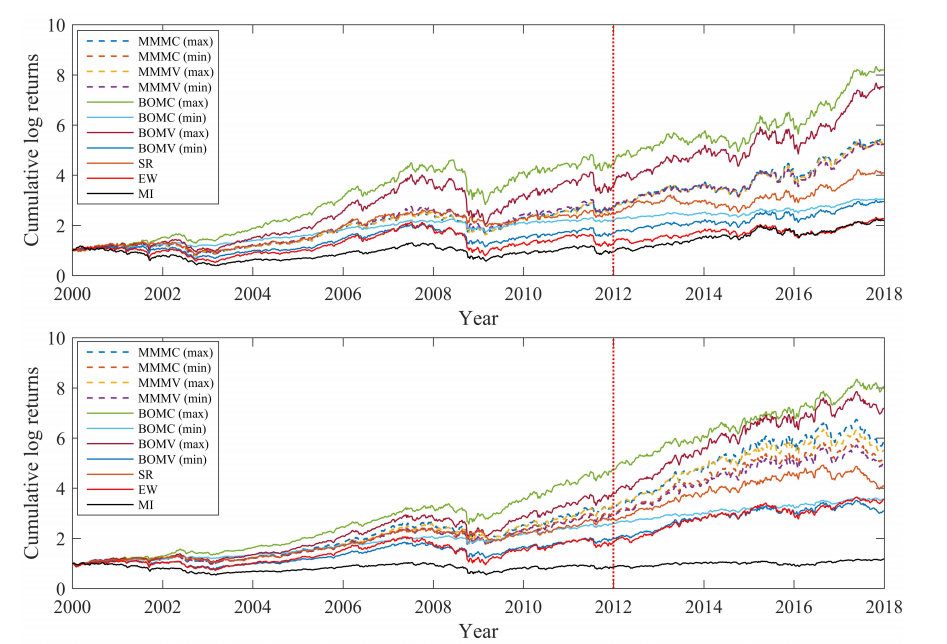
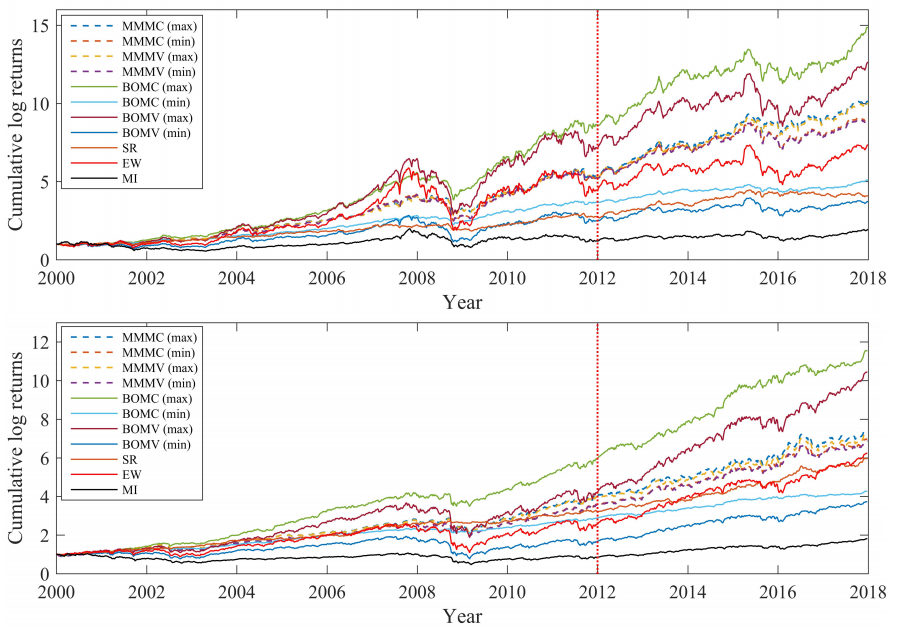
Fig.18. 基于HDAX(第一个子图)、FTSE(第二个子图)、HSI(第三个子图)和SP500(最后一个子图)数据集的不同投资组合的累积对数回报。
2000年至2011年底的曲线属于样本内检验,其余属于样本外检验(即以垂直红色虚线分隔)。其中MMMV (max)和MMMV (min)分别表示基于MV公式的年化收益最大和最小的最优minimax投资组合,BOMV (max)和BOMV (min)分别表示基于MV公式的年化收益最大和最小的最优双目标投资组合,MMMC (max)和MMMC (min)分别表示基于均值- cvar公式的年化收益最大和最小的最优minimax投资组合。BOMC (max)和BOMC (min)分别表示基于均值- cvar公式的年化收益最大和最小的最优双目标投资组合。可以看出,极大极小组合在每个数据集中具有相似的趋势,其累积对数收益与双目标组合相比差异相对较小。因此,双目标投资组合一方面在每个数据集上都优于其他投资组合,但另一方面,它们在富时指数、恒生指数和标准普尔500指数数据集上的表现可能不如其他投资组合
还需要指出的是,在2008年的金融危机中,全球股市都出现了大幅下跌。
如图所示,所有的投资组合都跟随每个市场的趋势。此外,在2007年第二季度至最后一个季度,由于本土资产泡沫,恒指的等权重投资组合表现良好。然而,股票市场的螺旋式下跌导致投资组合在随后一年的累计对数回报方面大幅下降。如图18所示,极小极大组合在同一时期表现出对急剧下跌的阻力(与其他组合相比波动较小)。2015年,恒指市场也出现了类似的情况。
V. CONCLUSION
本文将协作神经动力学方法应用于基于极大极小和双目标组合优化问题的组合选择。神经动力学方法被证明是全局收敛的最优投资组合在四个选定的市场。对比研究表明,基于均值cvar的双目标投资组合优化神经动力学方法优于其他方法
此外,极大极小组合的结果对权重不太敏感,而双目标组合在高风险水平上产生较高的年化收益。
许多途径可供进一步调查。未来的工作可能包括发展神经动力学方法,以实现基数约束、多时期和多层次的投资组合优化,以及考虑其他金融活动(如期权定价)的投资组合优化。























 8011
8011











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










