【学习】双三相永磁同步电机弱磁控制

 1.引言  

   对于电动车用永磁电机，需要具有较高的功率密度，要求电机不仅在恒功率工作区具有良好的工作特性，在弱磁工作区也需要有较宽的弱磁调速范围。 概括地说，可以从两个方面提高电机的弱磁输出能力。

  （1）优化电机结构，即通过改善磁路提高电机的弱磁能力[46]。 从本质上说，凸极电机较隐极电机具有更优异的弱磁性能。通过优化改进电机的电磁结构，也可以大幅提高电机弱磁扩速的能力。以上特殊结构的电机加工工艺更加复杂，但均在不同程度上提高了电机的弱磁能力，对于高性能需 求的场合具有非常广阔的应用前景。

 （2）通过控制算法实现优化的弱磁控制。 基本思路是在原本控制策略的基础上，通过算法对电机的直轴、交轴电流合理分配，利用直轴电枢反应削弱励磁磁场，以达到弱磁升速的目的，但这种 同时增加了电机的铜损，并且较大的负直轴电流将可能造成永磁体的不可逆去磁，对电机造成严重影响。这种方式目前应用更加广泛，也更容易实现，但难以极大程度地提高电机的弱磁调速范围，适用于一般性能需求的普及应用的场合。

2.1.双三相永磁同步电机弱磁控制实现

       对于双三相电机，经过矢量空间解耦变换后 o1-o2 子平面恒为零，故定子 电压矢量仅取决于α-β子平面和 z1-z2 子平面。当采用 SVPWM 调制方式时， 易得各子平面电压矢量应满足：

式中 Vr ——α-β子平面电压合成矢量；Vrz——z1-z2 子平面电压合成矢量； Udc——母线电压。 

      将四维电流矢量控制变为二维电流 矢量控制，即对 z1-z2 谐波子平面进行开环控制，如图 1，并设置其电压给定为零，从而进一步提高电压调制范围。在上述调制方式下，双三相电机α-β子平面的电压矢量满足：

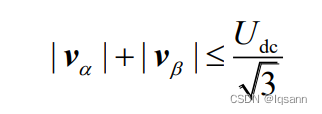
 2.2.双三相永磁同步电机弱磁控制约束条件

       通过将四维电流矢量控制和二维电流矢量控制相结合，双三相电机和传统三相电机的电压调制模型相统一。因此，在分析双三相电机的电压极限圆和电流极限圆时，就可以得到完全类似的结论：

式中 ulim——逆变器可输出的最大电压。 

式中 ilim——逆变电路可承受的最大电流。 

       电机的输出特性同时受逆变器母线电压的限制以及功率器件极限电流的限 制，如上两式。对于表贴式的永磁同步电机，其电压极限圆为和电机转 速相关的一族同心圆，且圆心坐标为(-ψf /Ld ,0) ，ψf /Ld称为同步电机的特征电流，电压极限圆随转速升高而向圆心收缩。而对于凸极永磁同步电机，由于其直轴电感小于交轴电感，其电压极限圆为长轴落在 d 轴的一族椭圆。电流极限圆的形状与电机参数无关，为圆形且半径不随转速变化，如图 2。电机工作在任意转速时，电流矢量的幅值和相位不能为任意值，应落在转速所对应的电压极限圆以及电流极限圆的内部，这称为电机工作点的约束条件。

3.1.全速段 MTPA 的弱磁控制算法设计 

        对于表贴式PMSM，在低速时通常采用id=0的矢量控制方式，也就是最大 转矩电流比（MTPA）控制方式，工作点落在图2中q轴上的线段OA上，其中 A点为电流极限圆与q轴的交点。此时，根据SPMSM的电压和电流极限圆的关系曲线，定义通过A点的电压极限圆所对应的速度为转折速度ωrt1，联立求得：

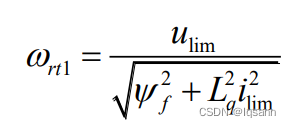
 根据转折速度将电机的工作区间分为：

（1）恒转矩区。当ω<ωrt1时，可控制电机在线段OA上的任意工作点处实现恒转矩控制，因此称转折速度以下的速度区间为电机的恒转矩控制区。如图 2，此时电压极限圆和电流极限圆相交于线段OA外部，所以最大输出转矩仅受到系统最大允许电流的限制，即可以在任意转速上输出最大转矩。

（2） 弱磁区。在电机转速不断增加至ω>ωrt1时，电压极限圆也将不断收缩，并与id=0控制曲线相交于电流极限圆的内部，故此时定子电流将受到电压极限的制约，交轴电流不能为任意大小。随转速不断升高，电压极限圆沿q轴方向快速收缩，若仍采用id=0的控制策略，电机可输出的最大电磁转矩明显下降，转矩的调节能力也因此降低，功率也比较低。若采用弱磁控制策略，当定子电流矢量沿id=0控制曲线达到电压极限时， 可通过适当增加负直轴分量的方法使工作点左移而偏离饱和，从而提高了转矩的输出范围。这种控制策略较原本的id=0控制策略增加了负的直轴分量，削弱了永磁体产生的励磁磁场，故称为弱磁控制。

3.1.1 现有弱磁方案的分析比较

       进行弱磁控制时，电机的q轴电流指令由转速外环确定，而d轴电流的大小决定了弱磁程度的深浅，可以根据控制目标选取不同的值，只要保证定子电流矢量在电压、电流极限圆内部，且直轴电流不超过永磁体去磁电流即可，因此 有多种弱磁控制策略。如何产生最简单高效的直轴去磁电流，即用最小的直轴电流满足电机转矩、转速输出要求，从而将不必要的损耗降至最小，是弱磁控制需要解决的问题。

       梯度下降法是实现弱磁控制的一种简单算法，其基本原理如图3。id和iq为矢量控制模块输出的电流给定信号，算法对电流调节器的输出电压进行采样，并求得其在极坐标系下的幅值，与逆变器最大输出电压值进行比较。当电流调节器未达到饱和时，差值△u 为正，意味着此时不需要弱磁，则弱磁补偿模块输出的补偿电流为零。当电机工作点落在电压极限圆之外时，差值△u 为负，则算法产生 α△u 的补偿电流，使工作点向电压极限圆内部的方向进行调整，从而实现了弱磁控制。

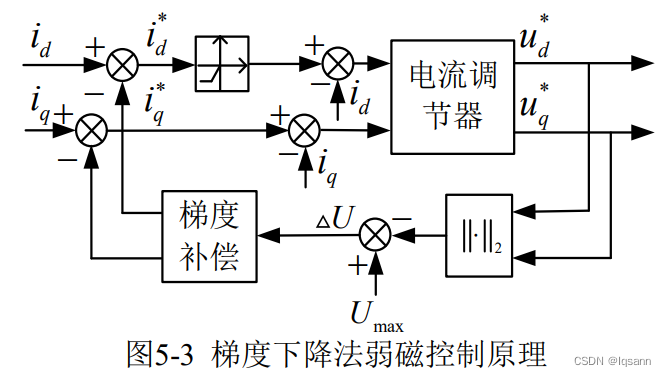
        梯度下降法需要计算转矩矢量和电压矢量的夹角，并判断电流下降的方向， 从而采取不同的算法计算补偿电流，因此算法在各区间内不一定连续变化。

        自动PI法就是用PI调节器代替上述算法中的梯度补偿环节，仍然采用电压反馈的方式确定弱磁时刻，其控制原理如图4。通过对PI调节器正向限幅为零，实现了弱磁时刻的的判断。算法仅对直轴电流进行修正，对于特征电流较小的电机 模型，不能保证工作点能够在电压极限圆内。

       超前角算法是基于以上算法的改进算法，其原理如图5所示。定义电流矢量和交轴正半轴夹角为超前角，若电压闭环PI调节器的输出正向限幅为零， 表示夹角为零，此时直轴电流为零，不进行弱磁。当电流矢量超出电压极限时， 通过改变超前角使得工作点沿指定轨迹运动，从而实现弱磁控制。

3.1.2 全速段 MTPA 算法 

       当电机的转速ω>ωrt1时，电机进入弱磁控制区。根据电压极限圆与交轴是否存在交点，可将弱磁区进一步分为完全弱磁区和不完全弱磁区。在完全弱磁区内，电压极限圆与交轴完全脱离，不再相交，若继续采用id=0控制策略电机将完全失去带载能力，故必须采取深度弱磁的算法。记通过原点的电压极限圆所对应的转速为ωrt2，通过电压极限圆方程可求得：

     在弱磁区，根据转速需要和电机带载情况，由弱磁模块计算直、交轴电流 指令。并且为避免转速在临界转速附近波动而频繁切换工作区导致的电流不稳定，需保证算法在各工作区之间圆滑过渡。 

（1）完全弱磁区（ωrt2<ω<ωrt3）

       当电机工作在完全弱磁区时，由于电压极限圆不再与q轴存在交点，故传 统的id=0控制控制策略完全失效，必须通过增加直轴电流分量，使得工作点向 电压极限圆偏移才能输出相应的转矩。定义转矩电流比函数：

      则根据式求偏导得：

 

       由于电流矢量落在第二象限，故转矩电流比的偏导均为正值，若要获得最 大转矩，应使得id在允许范围内取其最大值，因此最大转矩电流比曲线落在第 二象限内电流极限圆包围的电压极限圆右半圆弧上。如图6，当电机转速为w 时，对应虚线所示的电压极限圆，此时最大转矩电流比曲线为粗实线部分的电压极限圆圆弧。最大转矩电流比控制策略充分的利用了母线电压，并且输出相同电磁转矩时，电机铜损也最小。 由于工作点落在电压极限圆上，故电流给定应满足电压极限圆方程，则直轴电流给定应为：

       式中 Rw——电压极限圆的半径，且 Rw=ulim/ w*Ld。

       当转速不断增加至ωrt3以后，电压极限圆与电流极限圆脱离，无论怎样给定弱磁电流，定子电流矢量都不能同时满足电压极限和电流极限的约束，故 ωrt3为弱磁控制可以实现的最高转速，为：

 

（2）不完全弱磁区（ωrt1<ω<ωrt2）

       当电机工作在不完全弱磁区时，其转速所对应的电压极限圆与交轴相交于电流极限圆内部。故当电机带轻载工作时，所需的电磁转矩较小，仍可以采用 id=0控制策略，省去了不必要的弱磁环节；而当负载较大时，则采用MTPA弱磁控制策略，从而使得电机在不同工作条件下均输出最优的性能。 当电机工作在完全弱磁区和不完全弱磁区的重载条件下时，算得的ida0，故可以通过ida的正负判断电机的带载状态，从而确定相应的控制策略，而不需要额外检测负载大小。 最终将计算得到的ida经正向限幅为零后作为直轴电流给定即可。由于两个弱磁区算法一致，此而保证了电流给定信号自然过渡。

[1] 李怡蒨. 电动车用双三相永磁同步电机 驱动控制技术的研究[D].