1、简介
理解SVM,咱们必须先弄清楚一个概念:线性分类器。
给定一些数据点,它们分别属于两个不同的类,现在要找到一个线性分类器把这些数据分成两类。如果用x表示数据点,用y表示类别(y可以取1或者-1,分别代表两个不同的类),一个线性分类器的学习目标便是要在n维的数据空间中找到一个超平面(hyper plane),这个超平面的方程可以表示为( wT中的T代表转置):
可能有读者对类别取1或-1有疑问,事实上,这个1或-1的分类标准起源于logistic回归。
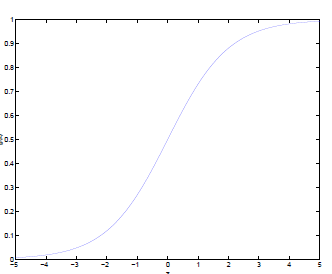
Logistic回归目的是从特征学习出一个0/1分类模型,而这个模型是将特性的线性组合作为自变量,由于自变量的取值范围是负无穷到正无穷。因此,使用logistic函数(或称作sigmoid函数)将自变量映射到(0,1)上,映射后的值被认为是属于y=1的概率。
假设函数
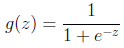 的图像是
的图像是
从而,当我们要判别一个新来的特征属于哪个类时,只需求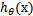 即可,若
即可,若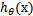 大于0.5就是y=1的类,反之属于y=0类。
大于0.5就是y=1的类,反之属于y=0类。
此外,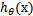 只和
只和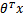 有关,
有关,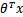 >0,那么
>0,那么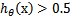 ,而g(z)只是用来映射,真实的类别决定权还是在于
,而g(z)只是用来映射,真实的类别决定权还是在于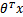 。再者,当
。再者,当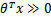 时,
时,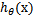 =1,反之
=1,反之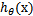 =0。如果我们只从
=0。如果我们只从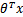 出发,希望模型达到的目标就是让训练数据中y=1的特征
出发,希望模型达到的目标就是让训练数据中y=1的特征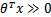 ,而是y=0的特征
,而是y=0的特征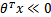 。Logistic回归就是要学习得到
。Logistic回归就是要学习得到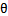 ,使得正例的特征远大于0,负例的特征远小于0,而且要在全部训练实例上达到这个目标。
,使得正例的特征远大于0,负例的特征远小于0,而且要在全部训练实例上达到这个目标。
接下来,尝试把logistic回归做个变形。首先,将使用的结果标签y = 0和y = 1替换为y = -1,y = 1,然后将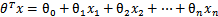 (
(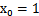 )中的
)中的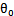
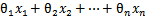 替换为
替换为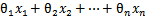 (即
(即 )。如此,则有了
)。如此,则有了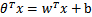 。也就是说除了y由y=0变为y=-1外,线性分类函数跟logistic回归的形式化表示
。也就是说除了y由y=0变为y=-1外,线性分类函数跟logistic回归的形式化表示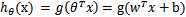 没区别。
没区别。
2、一个例子
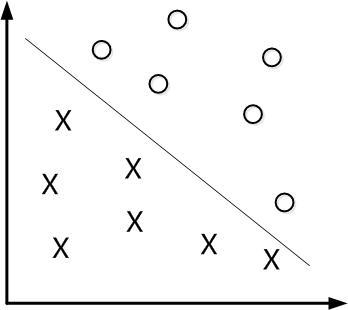
下面举个简单的例子,如下图所示,现在有一个二维平面,平面上有两种不同的数据,分别用圈和叉表示。由于这些数据是线性可分的,所以可以用一条直线将这两类数据分开,这条直线就相当于一个超平面,超平面一边的数据点所对应的y全是 -1 ,另一边所对应的y全是1。
这个超平面可以用分类函数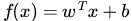
注:有的资料上定义特征到结果的输出函数
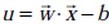 ,与这里定义的
,与这里定义的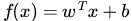 实质是一样的。为什么?因为无论是
实质是一样的。为什么?因为无论是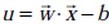 ,还是
,还是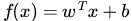 ,不影响最终优化结果。下文你将看到,当我们转化到优化
,不影响最终优化结果。下文你将看到,当我们转化到优化 (有一朋友飞狗来自Mare_Desiderii,看了上面的定义之后,问道:请教一下SVM functional margin 为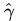
换言之,在进行分类的时候,遇到一个新的数据点x,将x代入f(x) 中,如果f(x)小于0则将x的类别赋为-1,如果f(x)大于0则将x的类别赋为1。
接下来的问题是,如何确定这个超平面呢?从直观上而言,这个超平面应该是最适合分开两类数据的直线。而判定“最适合”的标准就是这条直线离直线两边的数据的间隔最大。所以,得寻找有着最大间隔的超平面。
3、最大间隔
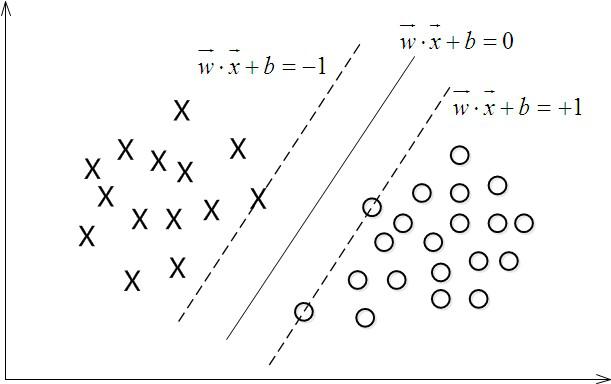
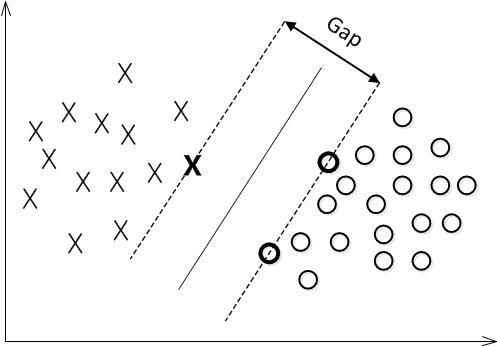
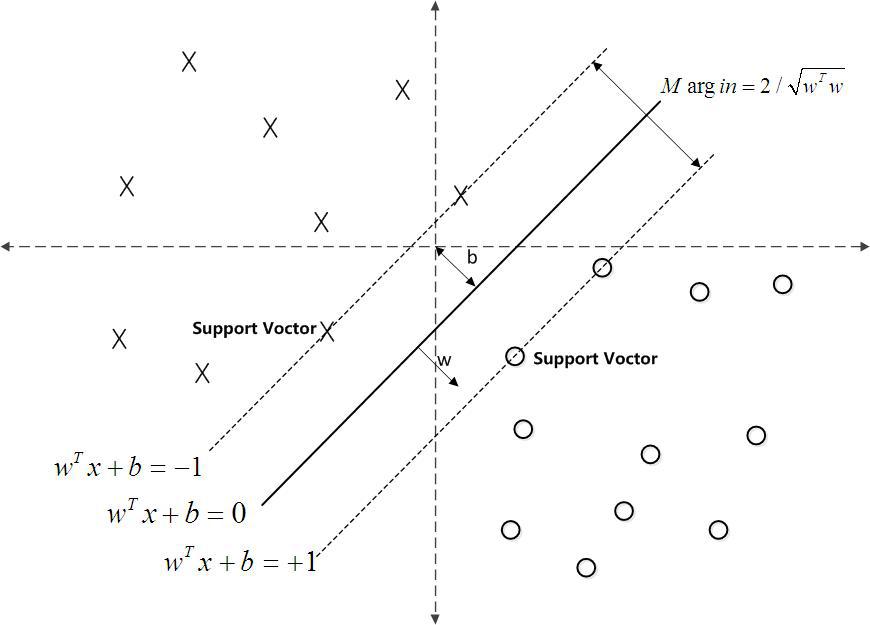
对一个数据点进行分类,当超平面离数据点的“间隔”越大,分类的确信度(confidence)也越大。所以,为了使得分类的确信度尽量高,需要让所选择的超平面能够最大化这个“间隔”值。这个间隔就是下图中的Gap的一半。
通过由前面的分析可知:函数间隔不适合用来最大化间隔值,因为在超平面固定以后,可以等比例地缩放w的长度和b的值,这样可以使得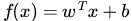
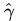
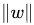
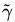
那么, 换言之,这里要找的最大间隔分类超平面中的“间隔”指的是几何间隔。
于是最大间隔分类器(maximum margin classifier)的目标函数可以定义为:
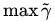
同时需满足一些条件,根据间隔的定义,有
其中,s.t.,即subject to的意思,它导出的是约束条件。
回顾下几何间隔的定义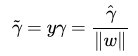
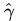
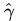
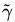
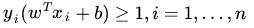
这个目标函数便是在相应的约束条件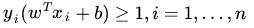
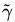
如下图所示,中间的实线便是寻找到的最优超平面(Optimal Hyper Plane),其到两条虚线边界的距离相等,这个距离便是几何间隔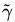
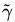
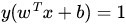
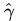
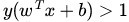
OK,到此为止,算是了解到了SVM的第一层,对于那些只关心怎么用SVM的朋友便已足够,不必再更进一层深究其更深的原理。
4、python实例
# -*- coding: utf-8 -*-
"""
Created on Wed Jul 13 16:31:19 2016
@author: irvingzhang
"""
import numpy as np
import pylab as pl
from sklearn import svm
#创建实例
np.random.seed(1)
X = np.r_[np.random.randn(20,2) - [2,2] ,np.random.randn(20,2) + [2,2]]
Y = [0] * 20 + [1] * 20
#分类器fit
clf = svm.SVC(kernel='linear')
clf.fit(X,Y)
#得到点和向量机的坐标
w = clf.coef_[0]
a = -w[0] / w[1]
xx = np.linspace(-5 , 5)
yy = a * xx - (clf.intercept_[0]) / w[1]
#画出经过支持向量机的超平面
b = clf.support_vectors_[0]
yy_down = a * xx + (b[1] - a * b[0])
b = clf.support_vectors_[-1]
yy_up = a * xx + (b[1] - a * b[0])
pl.plot(xx,yy,'k-')
pl.plot(xx,yy_down,'k--')
pl.plot(xx,yy_up,'k--')
pl.scatter(clf.support_vectors_[:,0],clf.support_vectors_[:,1],s=80,facecolors='none')
pl.scatter(X[:,0],X[:,1],c=Y,cmap=pl.cm.Paired)
pl.axis('tight')
pl.show()
结果展示:








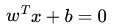
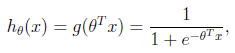
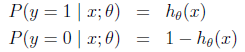
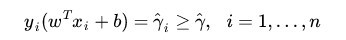
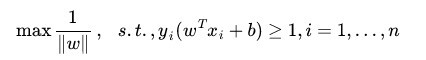















 7487
7487

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








