导航过程中的坐标系转换（n系转b系）

目录

一、问题引出

二、坐标系定义

2.1导航坐标系（系）

2.2载体坐标系（系）

三、用欧拉角表示旋转矩阵

四、代码实现

五、任务实现

---

一、问题引出

        最近在做一个课程项目，需要将卫星信息和惯导信息松组合解算之后的结果转换到b系之下(因为松组合结果是n系下的)，建立起时间和行驶里程之间的关系。则实现过程中存在一个坐标系转换的问题，在这里进行一个深入探讨。代码附在下文。

图1 松组合解算结果（n系）示意图

二、坐标系定义

        首先在这里介绍一下导航坐标系(系)和载体坐标系(系之间的区别和联系)：

2.1导航坐标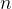系（系）

        导航坐标系的中心位于导航对象的中心或者质心上，轴沿着载体当前所在位置的法线方向，而轴和轴则沿着当前所在位置的经线和纬线的切线方向。       

        当地导航坐标系存在多种定义方式，包括“东-北-天”、“北-东-地”、“北-西-天”等右手直角坐标系。经过不断尝试，发现国外和国内牛小骥老师团队等采用的是“北-东-地”，而严工敏老师等团队更多地采用“东-北-天”坐标系。

        私认为“北-东-地”（NED）坐标系更加好用，故本文使用 “北-东-地”(NED)坐标系：轴平行于当地水平面指向正北，轴平行于当地水 平面指向正东，轴垂直于当地水平面向下，三轴构成右手系，如下图所示：

图2：“北-东-地”（NED）坐标系（n系）示意图

（注：图片来自知乎：城堡里学无人机：无人机导航之玩转坐标系 - 知乎 (zhihu.com)）

2.2载体坐标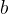系（系）

        载体坐标系的中心同样位于载体的中心或者质心位置，但是区别在于载体坐标系与载体固连在一起，通常定义为 “前右下”：轴沿载体纵轴指向载体前进方向，轴垂直于轴指向载体右侧， 轴与轴和轴垂直并构成右手系。

        对于角运动来说，x轴又称为横滚轴，y轴又称为俯仰轴，z轴又称为航向轴。从一个轴的正向看向负向，那么相对于这个轴的逆时针方向旋转为正，顺时针方向旋转为负。

图3：载体坐标系（b系）示意图

（注:图片来自CSDN：ROS【IMU】姿态检测与解算_ros imu-CSDN博客） 

三、用欧拉角表示旋转矩阵

        已知松组合解算出来的结果位于n系之下，而解算所得到的姿态角结果:roll，pitch，yaw，也是系相对于系之间的角度差异，可以将系设定为动坐标系，而系设定为参考系，则在某一时刻载体的位置向量在系和系下可分别记作：和。

        根据姿态角，我们可以通过三次定轴旋转来完成系到系的转化，设定分别绕轴、轴、轴进行旋转。首先第一次转动是系的坐标轴绕其轴转动角，此时设定系转动到系的位置，则向量在系和系之间的投影转化关系为：

        第二次转动，系绕其轴转动角。此时系到系的位置，向量在系到系之间的投影变换关系为：

         第三次转动，系绕其轴转动角。此时系转到系的位置，向量在系与系之间的投影变换关系为：

        将上面三个式子联立我们可以得到位置向量从系到系之间的投影变化关系：

（注：在这里由于篇幅限制采用简写形式，） 

        在给出吗，明确的旋转顺序情况下（），此处将系到系之间旋转矩阵简写为。

四、代码实现

        本次实现本来打算采用C++实现坐标转换操作，但是感觉实现过程中存在一些问题，在这里跟大家分享一下：根据Eigen库中的函数说明，本来打算采用库函数来完成坐标系的转化，经过查阅相关的知识点采用了如下的代码：

        设定初始状态如下：

class Point
{
public:
	double begin_time = 0;
	double emd_time = 0;
	double BLH[3] = { 0 };
	double Vned[3] = { 0 };
	double roll = 0;
	double pitch = 0;
	double yaw = 0;
    
    Point(double roll,double pitch,double yaw);//内部有单位转化，目标单位rad
};

         利用Eigen库函数进行调整求解旋转矩阵：

#include <iostream>  
#include <Eigen/Dense>  
#include "Point.h"
  
int main() {  
    // 定义姿态角  
    Point pot(0.71553,-0.08326,61.04575);  
  
    // 使用Eigen::AngleAxis创建旋转矩阵  
    Eigen::Matrix3d R_roll = Eigen::AngleAxisd(pot.roll, Eigen::Vector3d::UnitX()).toRotationMatrix();  
    Eigen::Matrix3d R_pitch = Eigen::AngleAxisd(pot.pitch, Eigen::Vector3d::UnitY()).toRotationMatrix();  
    Eigen::Matrix3d R_yaw = Eigen::AngleAxisd(pot.yaw, Eigen::Vector3d::UnitZ()).toRotationMatrix();  
  
    // 组合旋转矩阵以表示完整的姿态  
    Eigen::Matrix3d R =  R_roll * R_pitch * R_yaw;  
  
    // 打印旋转矩阵  
    std::cout << "Rotation Matrix:\n" << R << std::endl;  
  
    return 0;  
}

输出结果显示最终的旋转矩阵为：

Rotation Matrix:
   0.484110581167337   -0.874947096540032   0.0102236714535674
   0.875005619139685    0.484057463218483 -0.00731701964345696
 0.00145316062377597   0.0124880166021163    0.999920965759568

        但是经过后续测试，发现这个求解出来的旋转矩阵是有问题的，我用matlab进行了二次验证，这是根据算法写出的旋转矩阵转化函数：

function cn2b=Cn2b(roll,pitch,yaw)
    roll=deg2rad(roll);
    pitch=deg2rad(pitch);
    yaw=deg2rad(yaw);
    dx=[1,0,0;
        0,cos(roll),sin(roll);
        0,-sin(roll),cos(roll)];
    dy=[cos(pitch),0,-sin(pitch);
        0,1,0;
        sin(pitch),0,cos(pitch)];
    dz=[cos(yaw),sin(yaw),0;
        -sin(yaw),cos(yaw),0;
        0,0,1];
    cn2b=dx*dy*dz;
end

在设定同样的参数之后进行测试，发现最终的旋转矩阵为：

Rotation Matrix:
   0.484110581167338   0.875005619139685  -0.001453160623776
  -0.874929526102488   0.484089220903979   0.012488016602116
   0.011630544092973  -0.004774167838967   0.999920965759568

 正好matlab也有相对应的旋转矩阵的函数库使用语法为

DCM = angle2dcm( yaw, pitch, roll, ’ZYX’ )

在给定欧拉角的同时必须指定对应的转轴顺序：

clc;
clear;

roll=0.71553;
pitch=0.08326;
yaw=61.04575;
%三个欧拉角，单位为deg

cn2b1=Cn2b(roll,pitch,yaw);
cn2b2=angle2dcm(deg2rad(yaw),deg2rad(pitch),deg2rad(roll),'zyx');% 按ZYX(321)形式定义的欧拉角

disp(cn2b1);
disp(cn2b2);

发现最终的旋转矩阵同样为： 

Rotation Matrix:
   0.484110581167338   0.875005619139685  -0.001453160623776
  -0.874929526102488   0.484089220903979   0.012488016602116
   0.011630544092973  -0.004774167838967   0.999920965759568

        由此发现Eigen库中的旋转矩阵构建方式可能并非跟之前推导的相一致，不能够直接沿用， 进一步探究Eigen库函数中的单轴旋转矩阵的构建：

// 使用Eigen::AngleAxis创建旋转矩阵  
    Eigen::Matrix3d R_roll = Eigen::AngleAxisd(pot.roll, Eigen::Vector3d::UnitX()).toRotationMatrix(); 

发现由此构建的绕轴旋转的旋转矩阵呈现似乎也与之前推导的不一致：

R_roll:
                  1                   0                   0
                  0   0.999922021515692 -0.0124880297874584
                  0  0.0124880297874584   0.999922021515692

按照matlab正常运算得到的绕轴旋转的旋转矩阵为：

R_roll:
   1.000000000000000                   0                   0
                   0   0.999922021515692   0.012488029787458
                   0  -0.012488029787458   0.999922021515692

 所以之后的话没有再采用Eigen库的库函数来实现坐标系的转换，统一通过matlab来完成。（具体Eigen库为啥出现这个偏差的原因没有进行进一步探讨，之后有空的话会进一步总结，如果大家知道的话也请不吝赐教）。

五、任务实现

        通过当前时刻的姿态角，可以计算出每个时刻的旋转矩阵，通过计算相邻时刻和下车辆在系的位置向量和，可以计算出两个时间间隔之间的车辆坐标差。

        之后将其左乘一个旋转矩阵就可以得到在相邻时刻和下车辆在b系下的行驶位置差异：

        

        在这里需要注意一点，转换后的系下的三个方向都不会为0，但是这个在汽车行驶过程中是不合理的，小车应该只有前向速度才是，侧向和垂向速度的产生更多的是因为噪声引起，所以在计算里程的时候应该只取前向的位置差异来做里程累积：

        如果文中有不合适的错误之处，欢迎大家批评指正！