常用不等式总结说明

本篇博文常见的不等式进行总结说明，其中包括马尔科夫不等式、切比雪夫不等式、詹森不等式、李雅普诺夫不等式、霍尔德不等式、柯西不等式、闵可夫斯基不等式等。

---

1.Markov’s Inequality

马尔科夫不等式把概率和数学期望联系到一起，给出了随机变量大于某整数的概率上界。

---

2.Chebyshev’s Inequality

Let $\xi$ be a random variable, and mean value be $\mu$, variance be ${\sigma }^2$. Then for any $\epsilon >0$
$$P(|\xi -\mu |\ge \epsilon )\le {\sigma }^2/{\epsilon }^2$$.

切比雪夫不等式是对一个（不知分布的）随机变量在一个范围内的概率进行估计，有意思的，切比雪夫是如上不等式发现者马尔科夫的老师。

---

3.Jensen’s Inequality

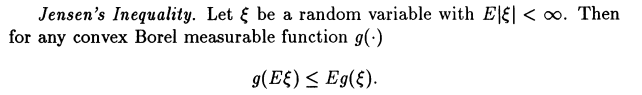
这是概率形式的詹森不等式。对于离散情形，只需求期望的操作变为求和操作。

4.Lyapunov’s Inequality

李雅普诺夫不等式反映了不同阶（绝对值）矩之间的不等式关系。

5.Holder’s Inequality

离散情形下，随机变量变为离散变量，期望（即，积分）变为求和。

6.Cauchy’s Inequality

如上为期望形势的柯西-施瓦茨不等式。矩阵形式的柯西-施瓦茨不等式为：$x^{T}y\le ||x||.||y||$.

7.Minkowsaki’s Inequality

离散形式的闵可夫斯不等式也即把随机变量改写为离散变量，积分改写为求和.

8.$C_r$ Inequality

$C_r$不等式说明统计意义上的估计，无法精确地得到真值.