（Visual Navigation）路径规划算法（二）Dijkstra改进 A*算法

• 上一文介绍了Dijkstra的基本思路和详细过程
• 接下来介绍一下Dijkstra的改进算法------A*算法

栅格地图

• 栅格地图取值原理
  

• 下面是构建一个栅格地图的基本过程

• 膨胀障碍物的意义是构建像上图的非自由区域
  

• 即直线移动的代价g（n）为1 斜边为根号2
  

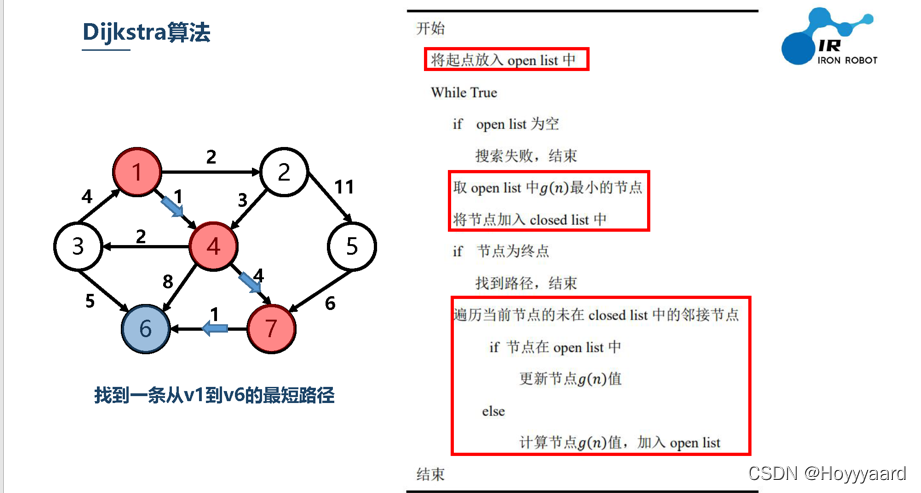
回顾Dijkstra算法

• 下图中的g（n）为节点到节点之间的代价
• eg：节点① 到节点④的代价为 1
• Dijkstra算法仅仅以g（n）为驱动函数
  

A*算法

A*算法引入h（n）为启发式函数

• 下图中为Dijkstra算法的结果 由于栅格地图中每个节点之间的g（n）都 == 1故Dijkstra算法会将收录节点向四周扩散 故结果显示整片地图上很多不相关的节点都会被收录进来 大大增加了工作量
  

伪代码对比

• 右边引入启发函数减少规划过程中不必要的节点收录
  

以欧氏距离（即起始点和目标点之间的直线距离）为启发式函数的结果

• 可以看到明显减少了很多不必要的节点的收录
  

A*算法应用的保证最优化要求

• 启发函数需要小于最短路径
• 下图为一个不正确的例子 假如到达节点②的h（2）= 6 那么算法就会收录③节点（代价为5+0）而不选择实际的最短路径②节点（代价为1+6）
  

当没有障碍物的时候可以更看出A*算法的优势

• 此时启发式函数h（n）为欧氏距离 故A*算法基本没有收录其他无关节点