[初识行列式]行列式的三种定义

本文根据张宇讲解线性代数整理

1. 行列式的性质定义(第一定义)

此种定义行列式的方法直接给出了行列式的几何含义,由数学家柯西提出:
假设有行列式$|\begin{array}{cc}{\alpha }_{11}& {\alpha }_{12}\\ {\alpha }_{21}& {\alpha }_{22}\end{array}|$,我们把$({\alpha }_{11},{\alpha }_{12})$和$({\alpha }_{21},{\alpha }_{22})$分别看成二维向量,并将其在直角坐标系中表示出来:

求向量所围成的四边形面积$$\begin{gathered} S=l\ast m\ast sin(\beta -\alpha ) \\ =l\ast m\ast (sin\beta cos\alpha -sin\alpha cos\beta ) \\ =l\ast \cos \alpha \ast m\ast sin\beta -l\ast sin\alpha \ast m\ast cos\beta \\ ={\alpha }_{11}\ast a_{22}-{\alpha }_{12}\ast {\alpha }_{21} \end{gathered}$$
所以行列式的结果就是以这两个向量为邻边的平行四边形的面积

将上述结论做线性推广就可以得到行列式的第一定义:n阶行列式是由n维向量组成的,其结果为以这n个向量为邻边的n维图形的体积

2. 行列式的逆序数定义法

• 逆序:在一个n级排列$i_1,i_2.....i_n$中,若$i_s>i_j$且$i_s$排在$i_j$前面,则称这两个数构成一个逆序
• 逆序数:在一个排列中,逆序的总数称为该排列的逆序数,如$\tau (231456)=3$

n(n>=2)阶行列式:
$$|\begin{array}{cccc}{a}_{11}& a_{12}& \dots \dots & a_{1n}\\ a_{21}& a_{22}& \dots \dots & a_{2n}\\ \dots \dots & \dots \dots & \dots \dots & \dots \dots \\ a_{n1}& a_{n2}& \dots \dots & a_{nn}\end{array}|={\Sigma }_{j_1,j_2....,j_n}(-1{)}^{\tau (j_1,j_2....,j_n)}{a}_{i{1}_1}a2j_2......a_{n{j}_n}$$

将上面这段翻译成人话主要是分成一下几个步骤:

1. ${\Sigma }_{j_1,j_2....,j_n}$表示对所有n个列下表排列求和,共有$n!$项之和
2. 每一项分别取自不同行,不同列的n个元素的乘积构成
3. 要先按照行下标顺排,再看列下标有几个逆序数,决定正负号

我们经常用的画图法就是属于用第二定义来求解,可见一般用其解决2阶或者3阶问题比较方便,大于3阶的则需要接下来的第三定义.

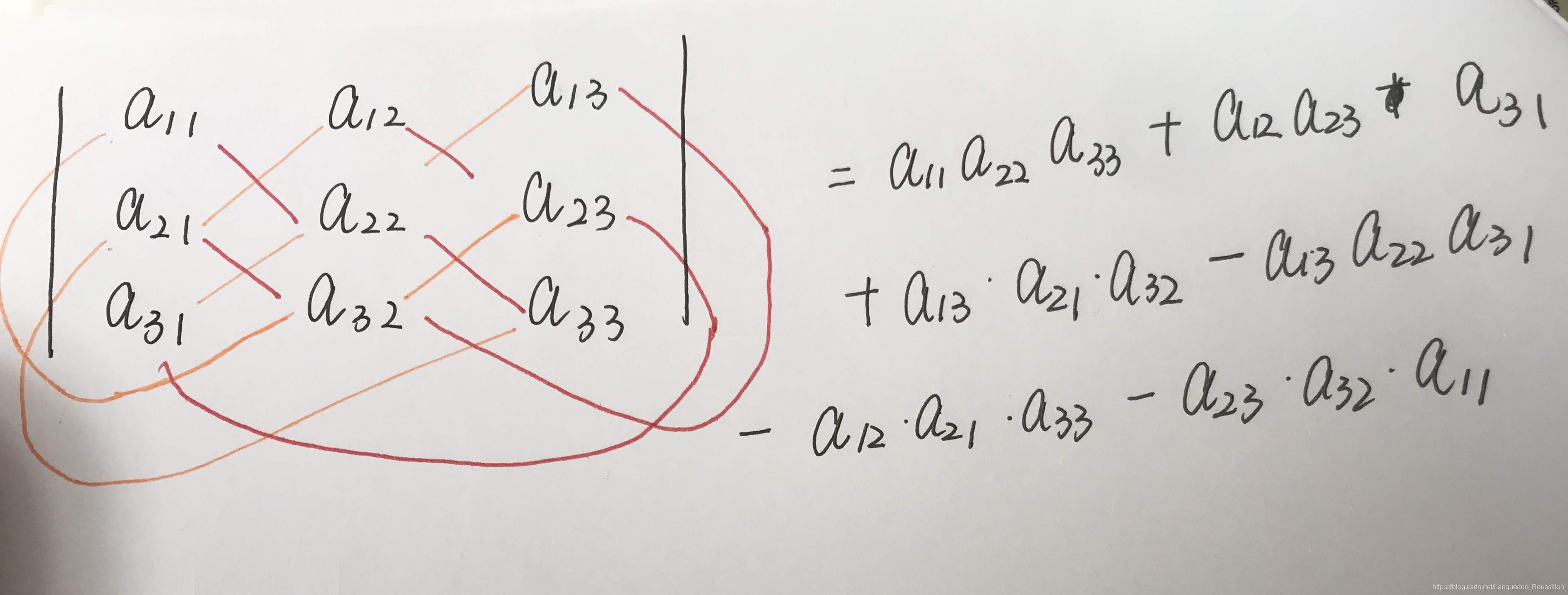
3. 行列式的展开定理(第三定义)

行列式的值等于行列式的某行(列)元素分别乘其相对应的代数余子式后再求和,其核心思想是降阶.