[深度学习]Part2 Logistic回归＆Softmax回归算法Ch05——【DeepBlue学习笔记】

LiongLoure

已于 2022-08-19 18:25:12 修改

阅读量294

点赞数

分类专栏：深度学习机器学习文章标签：回归深度学习学习

于 2022-06-26 19:53:33 首次发布

本文链接：https://blog.csdn.net/LiongLoure/article/details/125472648

版权

机器学习同时被 2 个专栏收录

21 篇文章 0 订阅

订阅专栏

深度学习

18 篇文章 0 订阅

订阅专栏

本文仅供学习使用（虽然叫回归算法，但实际上解决的是分类问题）

Logistic回归＆Softmax回归算法Ch05

1. Logistic回归
2. Softmax回归
3. 总结
4. 代码
5. 补充

1. Logistic回归

$\ln y={{\theta }^{T}}x$ ，这个就是对数几率回归（log-linear regression），实际上是在试图让 ${{e}^{{{\theta }^{T}}x}}$ 逼近y，在形式上仍是线性回归，但实际上已是在求取输入空间到输出空间的非线性函数映射，，更一般地，可以考虑单调可微函数 $g(\cdot )$ ，令 $y={{g}^{-1}}({{\theta }^{T}}x)$ ，这样得到的模型称为“广义线性模型”(generalized linear model)，其中 $g(\cdot )$ 称为联系函数（link function），显然，对数线性回归是广义线性模型在 $g(\cdot )=\ln (\cdot )$ 时的特例。

考虑分类任务，：只需找到一个单调可微函数将分类任务的真是标记y与线性回归模型的预测值联系起来，即将实值z转换为0/1值，最理想的是“单位阶跃函数”（unit-step function），亦称Heaviside函数；而单位阶跃函数不连续，因此不用直接使用 ${{g}^{-1}}(\cdot )$ ，因此需要找到一定程度上近似的“替代函数”（surrogate function），并且希望它单调可微——即对数几率函数（logistic function）

概率： $P\in (0,1)$
几率： $odds=\frac{P}{1-P}\in (0,+\infty )$

为了方便建立 ${{\theta }^{T}}x$ ，可对几率取 ln函数，得到对数几率（log odds，亦称logit）使其值域属于（0，+∞），即： ${{\theta }^{T}}x=\ln (\frac{P}{1-P})\Rightarrow P=\frac{1}{{{e}^{{{-\theta }^{T}}x}}+1}$
上式实际上实在用线性回归模型的预测结果去逼近真实标记的对数几率，其对应的模型称为“对数几率回归”（logistic regression，亦称logit regression）
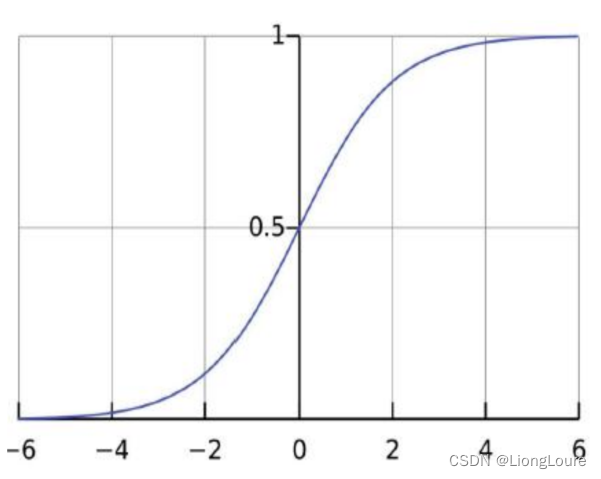
在逻辑回归中，线性模型被包含在一个逻辑函数（也叫做sigmoid函数）中：
Logistic/sigmoid函数

$P={{h}_{\theta }}(x)=\frac{1}{{{e}^{-{{\theta }^{T}}x}}+1}=g({{\theta }^{T}}x)$

在这里插入图片描述
$g(z)=\frac{1}{{{e}^{-z}}+1}\Rightarrow g(z)'=(\frac{1}{{{e}^{-z}}+1})'=\frac{{{e}^{-z}}}{{{({{e}^{-z}}+1)}^{2}}}=\frac{1}{{{e}^{-z}}+1}\cdot (1-\frac{1}{{{e}^{-z}}+1})=g(z)\cdot (1-g(z))$
逻辑函数的作用就是把函数的输出值限定在0和1之间，这样才能被解释为概率——它是直接对分类可能性进行建模，无需事先假设数据分布，这样就避免了假设分布不准确所带来的问题；它不是仅预测出“类别”，而是可得到近似概率预测，这对许多需利用概率辅助决策的任务很有用——对数几率回归求解的目标函数时任意阶可导的凸函数

1.1 Logistic回归及似然函数

from sklearn.linear_model import LogisticRegression

假设对于二分类问题，y=1时的概率为P，y=0时的概率为1-P，即： $P(y=1|x;\theta )={{h}_{\theta }}(x),P(y=0|x;\theta )=1-{{h}_{\theta }}(x)$
可得： $P(y|x;\theta )={{({{h}_{\theta }}(x))}^{y}}{{(1-{{h}_{\theta }}(x))}^{1-y}}$

似然函数： $L(\theta )=P(\vec{y}|x;\theta )=\prod\limits_{i=1}^{m}{P({{y}^{(i)}}|{{x}^{(i)}};\theta )}=\prod\limits_{i=1}^{m}{{{({{h}_{\theta }}({{x}^{(i)}}))}^{{{y}^{(i)}}}}{{(1-{{h}_{\theta }}({{x}^{(i)}}))}^{1-{{y}^{(i)}}}}}$

对数似然函数： $l(\theta )=\ln L(\theta )=\sum\limits_{i=1}^{m}{({{y}^{(i)}}\ln ({{h}_{\theta }}({{x}^{(i)}})+(1-{{y}^{(i)}})\ln (1-{{h}_{\theta }}({{x}^{(i)}}))}$

1.2 最大似然/极大似然函数的随机梯度

$\frac{\partial l(\theta )}{\partial {{\theta }_{j}}}=\sum\limits_{i=1}^{m}{(\frac{{{y}^{(i)}}}{h({{x}^{(i)}})}-\frac{1-{{y}^{(i)}}}{1-h({{x}^{(i)}})})}\cdot \frac{\partial h({{x}^{(i)}})}{\partial {{\theta }_{j}}}=\sum\limits_{i=1}^{m}{(\frac{{{y}^{(i)}}}{g({{\theta }^{T}}{{x}^{(i)}})}-\frac{1-{{y}^{(i)}}}{1-g({{\theta }^{T}}{{x}^{(i)}})})}\cdot \frac{\partial g({{\theta }^{T}}{{x}^{(i)}})}{\partial {{\theta }_{j}}}$

$\frac{\partial l(\theta )}{\partial {{\theta }_{j}}}=\sum\limits_{i=1}^{m}{(\frac{{{y}^{(i)}}}{g({{\theta }^{T}}{{x}^{(i)}})}-\frac{1-{{y}^{(i)}}}{1-g({{\theta }^{T}}{{x}^{(i)}})})}\cdot g({{\theta }^{T}}{{x}^{(i)}})(1-g({{\theta }^{T}}{{x}^{(i)}}))\frac{\partial {{\theta }^{T}}{{x}^{(i)}}}{\partial {{\theta }_{j}}}$

$\frac{\partial l(\theta )}{\partial {{\theta }_{j}}}=\sum\limits_{i=1}^{m}{({{y}^{(i)}}\cdot (1-g({{\theta }^{T}}{{x}^{(i)}}))-(1-{{y}^{(i)}})\cdot g({{\theta }^{T}}{{x}^{(i)}}))}\cdot x_{j}^{(i)}=\sum\limits_{i=1}^{m}{({{y}^{(i)}}-g({{\theta }^{T}}{{x}^{(i)}}))}\cdot x_{j}^{(i)}$

1.3 极大似然估计与Logistic回归目标函数

由于在极大似然估计中，当似然函数最大的时候模型最优；而在机器学习领域中，目标函数最小的时候，模型最优；故可以使用似然函数乘以 -1 的结果作为目标函数：
$l(\theta )=\ln L(\theta )=\sum\limits_{i=1}^{m}{({{y}^{(i)}}\ln ({{h}_{\theta }}({{x}^{(i)}})+(1-{{y}^{(i)}})\ln (1-{{h}_{\theta }}({{x}^{(i)}}))}$

$loss=-l(\theta )=-\sum\limits_{i=1}^{m}{({{y}^{(i)}}\ln ({{h}_{\theta }}({{x}^{(i)}})+(1-{{y}^{(i)}})\ln (1-{{h}_{\theta }}({{x}^{(i)}}))}=\sum\limits_{i=1}^{m}{(-{{y}^{(i)}}\ln ({{h}_{\theta }}({{x}^{(i)}})-(1-{{y}^{(i)}})\ln (1-{{h}_{\theta }}({{x}^{(i)}}))}$

1.4 θ参数求解

Logistic回归θ参数的求解过程为(类似梯度下降方法):

批量梯度下降：
${{\theta }_{j}}'={{\theta }_{j}}+\alpha \sum\limits_{i=1}^{m}{({{y}^{(i)}}-{{h}_{\theta }}({{x}^{(i)}}))}\cdot x_{j}^{(i)}$

随机梯度下降：
${{\theta }_{j}}'={{\theta }_{j}}+\alpha ({{y}^{(i)}}-{{h}_{\theta }}({{x}^{(i)}}))x_{j}^{(i)}$

虽然上述为二分类问题，但Logistic回归算法有多分类的形式

1.5 算法设置

创建一个逻辑回归的对象：logis = LogisticRegression()
训练模型：model = logis.fit(features_standardized,target)
预测分类：model.predict(new_observation)
查看预测的概率：model.predict_proba(new_observation)

独立来看，逻辑回归只是二元分类器，这意味着他不能处理两个分类的目标向量。但是逻辑回归有两个巧妙的拓展可以解决这个问题：

一对多(One-vs-Rest,OVR)：在这种逻辑回归中，对于每一个分类我们都会训练一个单独的模型来判断观察值是不是属于这个分类（假设每一个分类问题是相互独立的）
多元逻辑回归(Multinomial Logistic Regression,MLR)：即Softmax回归，使用predict_proba方法预测概率，更可靠，使用逻辑回归时默认选择为OVR（multi_class='ovr'），将其参数改为‘multinomial’，改为使用MLR

2. Softmax回归

• softmax回归是logistic回归的一般化，适用于K分类的问题，针对于每个类别都有一个参数向量θ，第k类的参数为向量θk，组成的二维矩阵为θk*n
• softmax函数的本质就是将一个K维的任意实数向量压缩（映射）成另一个K维的实数向量，其中向量中的每个元素取值都介于（0，1）之间。
• softmax回归概率函数为：

$P(y=k|x;\theta )=\frac{{{e}^{\theta _{k}^{T}x}}}{\sum\limits_{l=1}^{K}{{{e}^{\theta _{l}^{T}x}}}},k=1,2,\cdots ,K$

采用指数函数进行归一化——本身为单调函数，且区别较大，方便求导

2.1 Softmax算法原理

${{h}_{\theta }}(x)=\left[ \begin{matrix} P({{y}^{(i)}}=1|{{x}^{(i)}};\theta ) \\ P({{y}^{(i)}}=2|{{x}^{(i)}};\theta ) \\ \vdots \\ P({{y}^{(i)}}=k|{{x}^{(i)}};\theta ) \\ \end{matrix} \right]=\frac{1}{\sum\limits_{l=1}^{K}{{{e}^{\theta _{l}^{T}x}}}}\left[ \begin{matrix} {{e}^{\theta _{1}^{T}x}} \\ {{e}^{\theta _{2}^{T}x}} \\ \vdots \\ {{e}^{\theta _{k}^{T}x}} \\ \end{matrix} \right]\Rightarrow \theta =\left[ \begin{matrix} {{\theta }_{11}} & {{\theta }_{12}} & \cdots & {{\theta }_{1n}} \\ {{\theta }_{21}} & {{\theta }_{22}} & \cdots & {{\theta }_{2n}} \\ \vdots & \vdots & \ddots & \vdots \\ {{\theta }_{k1}} & {{\theta }_{k2}} & \cdots & {{\theta }_{kn}} \\ \end{matrix} \right]$

2.2 Softmax算法损失函数

$J(\theta )=-\frac{1}{m}\sum\limits_{i=1}^{m}{\sum\limits_{j=1}^{k}{I({{y}^{(i)}}=j)\ln (\frac{{{e}^{\theta _{j}^{T}x}}}{\sum\limits_{l=1}^{K}{{{e}^{\theta _{l}^{T}x}}}})}}$ ，其中： $I({{y}^{(i)}}=j)=\left\{ \begin{matrix} 1 & {{y}^{(i)}}=j \\ 0 & {{y}^{(i)}}\ne j \\ \end{matrix} \right.$

2.3 Softmax算法梯度下降法求解

$\frac{\partial J(\theta )}{\partial {{\theta }_{j}}}=\frac{\partial }{\partial {{\theta }_{j}}}(-I({{y}^{(i)}}=j)\ln (\frac{{{e}^{\theta _{j}^{T}{{x}^{(i)}}}}}{\sum\limits_{l=1}^{K}{{{e}^{\theta _{l}^{T}{{x}^{(i)}}}}}}))=\frac{\partial }{\partial {{\theta }_{j}}}(-I({{y}^{(i)}}=j)(\theta _{j}^{T}{{x}^{(i)}}-\ln (\sum\limits_{l=1}^{K}{\theta _{l}^{T}{{x}^{(i)}}})))$

$\frac{\partial J(\theta )}{\partial {{\theta }_{j}}}=-I({{y}^{(i)}}=j)(1-\frac{{{e}^{\theta _{j}^{T}{{x}^{(i)}}}}}{\sum\limits_{l=1}^{K}{{{e}^{\theta _{l}^{T}{{x}^{(i)}}}}}}){{x}^{(i)}}$
批量梯度下降：
${{\theta }_{j}}'={{\theta }_{j}}+\alpha \sum\limits_{i=1}^{m}{I({{y}^{(i)}}=j)(1-P({{y}^{(i)}}=j|{{x}^{(i)}};\theta ))}{{x}^{(i)}}$
随机梯度下降：
${{\theta }_{j}}'={{\theta }_{j}}+\alpha I({{y}^{(i)}}=j)(1-P({{y}^{(i)}}=j|{{x}^{(i)}};\theta )){{x}^{(i)}}$

3. 总结

• 线性模型一般用于回归问题，Logistic和Softmax模型一般用于分类问题
• 求θ的主要方式是梯度下降算法，梯度下降算法是参数优化的重要手段，主要是SGD，适用于在线学习以及跳出局部极小值
• Logistic/Softmax回归是实践中解决分类问题的最重要的方法
• 广义线性模型对样本要求不必要服从正态分布、只需要服从指数分布簇(二项分布、泊松分布、伯努利分布、指数分布等)即可；广义线性模型的自变量可以是连续的也可以是离散的。
• 在一个超大数据集上训练一个简单的分类模型可以使用随机平均梯度（Stochastic Average Gradient，SAG）solver来训练一个逻辑回归模型：solver='sag'
• 对于不均衡的分类，且预处理没有解决这个问题时，可以使用class_weight参数给分类设置权重class_weight='balanced'，权重值与分类的出现频率的倒数相关：
${{w}_{j}}=\frac{n}{k{{n}_{j}}}$ ，wj是分类j的权重，n是观察值的数量，nj是属于分类j的观察值的数量，k是分类的总数。

4. 代码

import pandas as pd
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import matplotlib as mpl


## 设置字符集，防止中文乱码
mpl.rcParams['font.sans-serif'] = [u'simHei']
mpl.rcParams['axes.unicode_minus'] = False

##读取数据
a = pd.read_csv('D:/datas/breast-cancer-wisconsin.data', header=None)
# print(a.head())
# print(a.info())  # object
# sys.exit(0)
# a = a.astype(np.int64)
###数据清洗
##缺失值的处理  1.删除这条（行）数据  2.填充 均值，0，众数，经验
a.replace('?', np.nan, inplace=True)
# a = a.replace('?',np.nan,inplace=False)
a = a.dropna(axis=0)
a = a.astype(np.int64)  ###转换数据类型
# print(a.info())
# sys.exit()
X = a.iloc[:, 1:-1]
Y = a.iloc[:, -1]
print(Y.value_counts())
# print(X)
# sys.exit()

x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=0.25, random_state=5)

logis = LogisticRegression()
"""
penalty='l2', 过拟合解决参数,l1正则或者l2正则 {'l1', 'l2', 'elasticnet', 'none'}, 
default='l2'；'newton-cg'、'sag' 和 'lbfgs' 求解器仅支持 l2 惩罚。'elasticnet' 仅由 'saga' 求解器支持。
如果为“无”（不受 liblinear 求解器支持），则不应用正则化。

dual=False, 
tol=1e-4, 梯度下降停止条件
C=1.0, 正则化强度的倒数；必须是正浮点数。较小的值指定更大的正则化 1/lamda
fit_intercept=True, 
intercept_scaling=1, 
class_weight=None, 类别权重，有助于解决数据类别不均衡的问题
random_state=None, 

solver='liblinear',  参数优化方式，当penalty为l1的时候，参数只能是：liblinear(坐标轴下降法)；
当penalty为l2的时候，参数可以是：lbfgs(拟牛顿法)、newton-cg(牛顿法变种)，seg(minibatch),
维度<10000时，lbfgs法比较好， 维度>10000时， cg法比较好，显卡计算的时候，lbfgs和cg都比seg快
【nlbfgs和cg都是关于目标函数的二阶泰勒展开】


max_iter=100, 最多的迭代次数
multi_class='ovr', 分类方式参数；参数可选: ovr(默认)、multinomial；这两种方式在二元分类问题中，效果是一样的；
在多元分类问题中，效果不一样；ovr: one-vs-rest， 对于多元分类的问题，先将其看做二元分类，分类完成后，
再迭代对其中一类继续进行二元分类；multinomial: many-vs-many（MVM）,即Softmax分类效果

verbose=0, 
warm_start=False, 
n_jobs=1
## Logistic回归是一种分类算法，不能应用于回归中(也即是说对于传入模型的y值来讲，不能是float类型，必须是int类型)
"""
logis.fit(x_train, y_train)
train_score = logis.score(x_train, y_train)
test_score = logis.score(x_test, y_test)
y_test_hat = logis.predict(x_test)
print(test_score, train_score)
plt.plot(range(len(x_test)), y_test, 'ro', markersize=4, zorder=3, label=u'真实值')
plt.plot(range(len(x_test)), y_test_hat, 'go', markersize=10, zorder=2, label=u'预测值')
plt.legend()
plt.show()

5. 补充

参考《机器学习》-周志华

线性模型形式简单、易于建模，但却蕴涵着机器学习中一些重要的基本思想。许多功能更为强大的非线性模型（nonlinear model）可在线性模型的基础上通过引入层级结构或高维映射而得。此外由于θ直观表达了各属性在预测中的重要性，因此线性模型有很好的可解释性（comprehensibility）