百面深度学习：基于度量学习的元学习模型

更多基础知识可以查看前文内容 《百面深度学习》之元学习

基于度量学习（Metric Learning）的元学习方法，是基于最邻近方法的元学习的延伸。

知识点： 灾难性忘却（catastrophic forgetting）、 度量学习、外部记忆、注意力机制

Q1 元学习中非参数方法相比于参数方法的优点？

• 非参数方法： 在新任务上没有参数学习的过程
• 参数方法：在新任务上需要继续微调模型

参数方法的缺点：

• 训练使得新任务的学习过程比较慢，达不到快速学习的目的，且不适合样本很少的情况。
• 微调过程会受到新任务自身携带的噪声等影响，让原先在$D_{meta-train}$上训练好的模型参数值被错误信息覆盖，这种现象称为灾难性忘却。

非参数方法的优点：

• 不依赖梯度下降的优化过程
• 不修改预训练的参数信息。新样本信息不会相互干扰，避免了灾难性忘却。
• 可以快速学习，尤其是适用于样本少的情况。

Q2 如何用度量学习和注意力机制来改造基于最邻近的元学习方法？

新模型结构：

1. 给定单个任务的数据集 D t a s k = { D t r a i n , D t e s t } D_{task} = \left\{D_{train},D_{test}\right\} Dtask​={Dtrain​,Dtest​}, 将$D_{train}$定义为一个由<样本，标签>对构成的支持集，视作一个外部记忆（external memory）
2. 预测$D_{test}$中的样本时，对这个外部记忆进行快速的查找，灵活的访问$D_{train}$的每一个样本。
3. 访问的方法采用软注意力（soft-attention）机制，这是一种形如加权平均的访问机制，完全可导，方便利用梯度下降进行端到端的学习。

对元学习进行建模：
元学习的泛函含义： 从单个任务t到该任务分类器函数的映射: 即$t\mapsto f(\cdot ,D_{train}^t;\Theta )$. 也就是说元学习会为每个任务生成一个分类器，不同任务基于不同的训练集，但共享元参数$\Theta$.

实现$f(\cdot ,D_{train}^t;\Theta )$的具体结构：

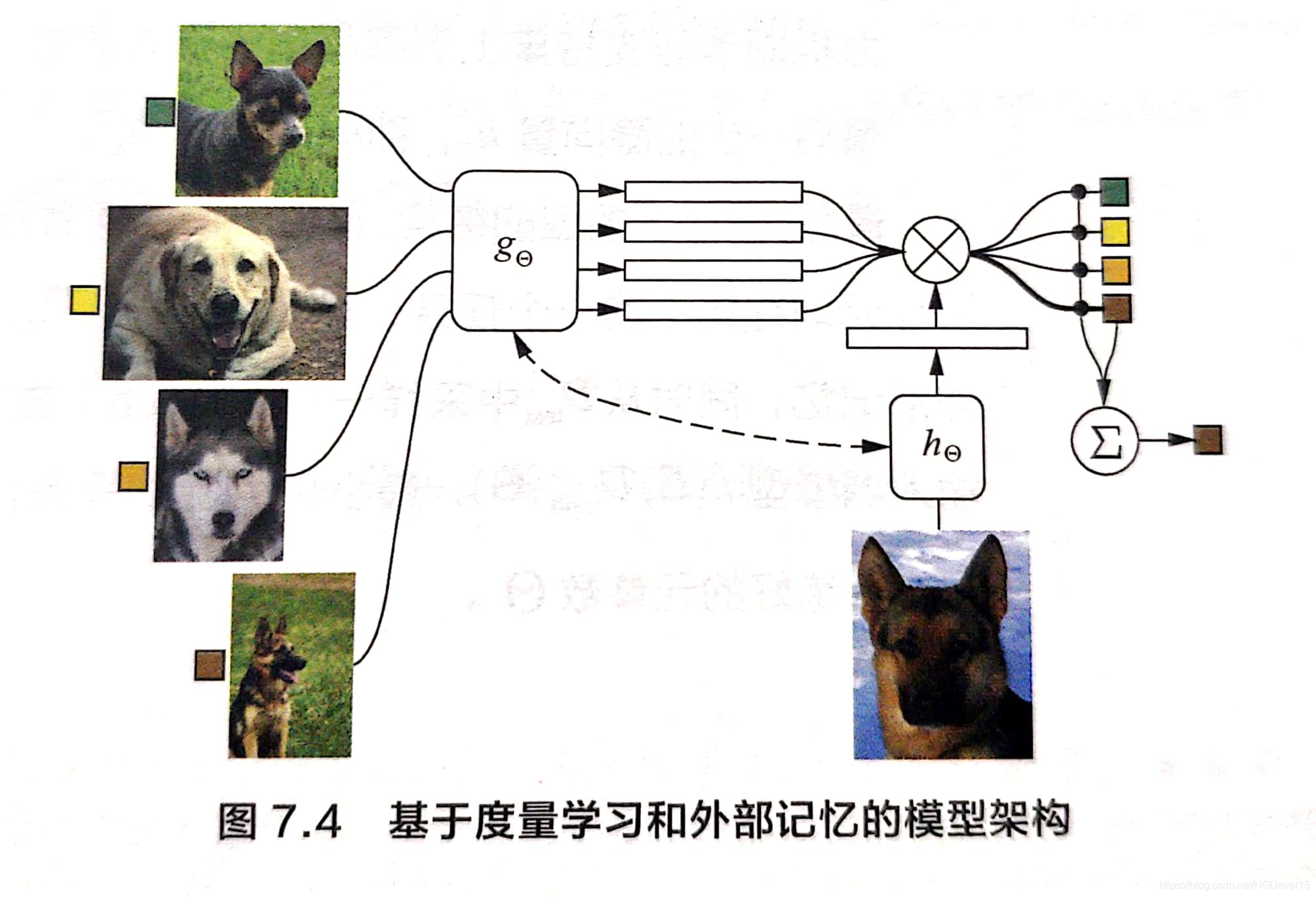
如何 7.4所示 $g_{\Theta }$ 和$h_{\Theta }$ 是两个计算嵌入向量的神经网络结构，前者负责计算训练样本的嵌入向量，后者负责计算测试样本的。 （二者也可以是同一个网络）。

• 基于训练样本的嵌入向量，构造外部记忆。 假设$z_i=g_{\Theta }(x_i)$为样本$x_i$的嵌入向量，对应的类别标签为$y_i$, 将$（z_i,y_i）$存储在记忆模块的一个槽中，访问时，基于$z_i$计算匹配权重，匹配返回$y_i$。 这样的记忆模块称为关联记忆（associative memory）。
• 对测试样本x，先计算他的嵌入向量$z=h_{\Theta }(x)$,再利用注意力机制访问记忆模块以获取最终的标签，公式为$$y=\sum _{i}a(z,z_i)y_i$$ , 其中$a（\cdot ）$可以是一个神经网络。

注意力机制的两两计算方法，本质是核方法（kernel method），所以也称为注意力核（attention kernel）

将整个训练集$D_{train}$作为支持集S 输入到网络， 即$g_{\Theta }(x_i,S)$ 和$h_{\Theta }(x,S)$, 这样嵌入网络就拥有了全局视野。

总结
明显缺点： 外部记忆的大小会随着支持集的样本数增大而增大，没有上限。