VIO-SLAM中的欧拉积分、中点积分与龙格－库塔积分

在 SLAM 系统中经常用到各种不同的数值积分方法，工程上最常见的有三种：欧拉积分（Euler method）、中点积分（Midpoint method）和龙格－库塔法积分（Runge–Kutta methods）。他们的区别就是如何用数值方法模拟一个斜率。这里简单总结如下：

一、欧拉积分

设有如下微分方程：

y′(t)=f(t,y(t))y'(t)=f(t,y(t))y′(t)=f(t,y(t))

并且 tnt_ntn​ 和 tn+1t_{n+1}tn+1​ 时刻的差为 tn+1−tn=Δtt_{n+1} - t_n = \Delta ttn+1​−tn​=Δt，则欧拉积分定义为：

yn+1=yn+Δt⋅f(tn,yn)y_{n+1}=y_n + \Delta t\cdot f(t_n, y_n)yn+1​=yn​+Δt⋅f(tn​,yn​)

也就是说用 t 时刻的斜率作为整个 t→t+Δtt\rightarrow t+\Delta tt→t+Δt 时刻的导数。

二、中点积分

设有如下微分方程：

y′(t)=f(t,y(t))y'(t)=f(t,y(t))y′(t)=f(t,y(t))

并且 tnt_ntn​ 和 tn+1t_{n+1}tn+1​ 时刻的差为 tn+1−tn=Δtt_{n+1} - t_n = \Delta ttn+1​−tn​=Δt，则显式中点积分定义为：

yn+1=yn+Δt⋅f(tn+12Δt,yn+12Δt⋅f(tn,yn))y_{n+1}=y_n + \Delta t\cdot f(t_n + \frac{1}{2} \Delta t, y_n + \frac{1}{2}\Delta t \cdot f(t_n, y_n))yn+1​=yn​+Δt⋅f(tn​+21​Δt,yn​+21​Δt⋅f(tn​,yn​))

则隐式中点积分定义为：

yn+1=yn+Δt⋅f(tn+12Δt,12(yn+yn+1))y_{n+1}=y_n + \Delta t\cdot f(t_n + \frac{1}{2} \Delta t, \frac{1}{2}(y_n + y_{n+1}))yn+1​=yn​+Δt⋅f(tn​+21​Δt,21​(yn​+yn+1​))

也就是说用 tn+12Δtt_n + \frac{1}{2} \Delta ttn​+21​Δt 时刻的斜率作为整个 t→t+Δtt\rightarrow t+\Delta tt→t+Δt 时刻的导数。

欧拉积分与中点积分都是一阶近似并没有本质不同，二者只是一阶导数所取位置不同，他们的性能也有差别，如下图所示，作为一阶积分近似方法来讲，中点积分有时会稍好一些（带来更快的收敛速度）。

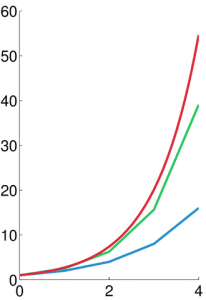
图示为方程 y′=y,y(0)=1y'=y, y(0)=1y′=y,y(0)=1 的数值积分。蓝色为欧拉法，绿色为中点法，红色为精确解 y=ety=e^{t}y=et。所用步长为 h=1.0。

三、龙格－库塔积分

龙格－库塔法（Runge-Kutta methods）是用于非线性常微分方程的解的重要的一类隐式或显式迭代法。在工程中最常用的是四阶龙格－库塔积分，也就是 RK4 积分，它的计算方式如下：

设有如下微分方程：

y′(t)=f(t,y(t))y'(t)=f(t,y(t))y′(t)=f(t,y(t))

并且 tnt_ntn​ 和 tn+1t_{n+1}tn+1​ 时刻的差为 tn+1−tn=Δtt_{n+1} - t_n = \Delta ttn+1​−tn​=Δt，则 RK4 积分定义为：

yn+1=yn+Δt6⋅(k1+2k2+2k3+k4)y_{n+1}=y_n + \frac{\Delta t}{6} \cdot (k_1 + 2k_2 + 2k3 + k_4)yn+1​=yn​+6Δt​⋅(k1​+2k2​+2k3+k4​)

其中：

k1是时间段开始时的斜率；
k2是时间段中点的斜率，通过欧拉法采用斜率k1来决定y在点tn + h/2的值；
k3也是中点的斜率，但是这次采用斜率k2决定y值；
k4是时间段终点的斜率，其y值用k3决定。
其数学公式如下：

k1=f(tn,yn)k_1 = f(t_n, y_n)k1​=f(tn​,yn​)
k2=f(tn+Δt2,yn+Δt2⋅k1)k_2 = f(t_n + \frac{\Delta t}{2}, y_n + \frac{\Delta t}{2} \cdot k_1)k2​=f(tn​+2Δt​,yn​+2Δt​⋅k1​)
k3=f(tn+Δt2,yn+Δt2⋅k2)k_3 = f(t_n + \frac{\Delta t}{2}, y_n + \frac{\Delta t}{2} \cdot k_2)k3​=f(tn​+2Δt​,yn​+2Δt​⋅k2​)
k4=f(tn+Δt,yn+Δt⋅k3)k_4 = f(t_n + \Delta t, y_n + \Delta t \cdot k_3)k4​=f(tn​+Δt,yn​+Δt⋅k3​)

从公式中可以看出两个中点的斜率具有更大的权重。

龙格－库塔法的示意图如下，它也是一种更高阶的逼近方法，通常也具有更好的逼近效果，总累计误差为 Δt4\Delta t^4Δt4 阶。

RK4 算法在 SLAM 中也有很好的应用，特别是 VIO 中的预积分部分，比如张腾将王京的 VI ORB SLAM2 代码改成 RK4 积分后，精度也得到了一定的提升：
https://github.com/RomaTeng/ORB-VINS_RK4

当然 RK4 算法比起欧拉积分、中点积分计算量要大不少，SLAM 中影响精度的地方非常多，仅靠 RK4 改进其对于精度的提升程度通常也不会特别大，不过对于速度要求不高而精度要求很高的场合还是值得尝试的。

参考文献
[1] https://en.wikipedia.org/wiki/Euler_method
[2] https://en.wikipedia.org/wiki/Midpoint_method
[3] https://en.wikipedia.org/wiki/Runge%E2%80%93Kutta_methods
[4] https://www.maplesoft.com/support/help/maple/view.aspx?path=Student%2FNumericalAnalysis%2FRungeKutta