
SHAP(SHapley Additive exPlanations)是一种用于解释任何机器学习模型输出的博弈论方法。它利用博弈论中的经典 Shapley 值及其相关扩展,将最优信用分配与局部解释联系起来。
一、为什么需要SHAP?
在机器学习模型的应用中,我们常遇到以下痛点:
黑箱模型的不可知性
像XGBoost、深度学习这样的复杂模型如同"黑盒子",即使预测准确率高,也无法直观理解其决策逻辑。例如医生使用AI诊断癌症,若无法解释为何模型判定某病人为高风险,将难以获得患者信任。
局部与全局解释割裂
传统特征重要性排序(如随机森林的feature_importance)只能告诉我们哪些特征整体重要,却无法解释"为什么某个特定样本被预测为阳性"。就像银行拒贷时,客户追问"我的收入明明达标,为何被拒?",传统方法无法给出具体答案。
忽略特征交互作用
部分依赖图(PDP)假设特征独立,但现实中特征往往存在强关联。例如预测房价时,"地段"和"学区"可能共同作用,单独分析每个特征会遗漏关键信息。
二、核心原理:博弈论基础、Shapley值、案例解释
1. 博弈论基础:合作博弈的公平分配法则
1.1 什么是博弈论?
博弈论(Game Theory)研究理性决策者在冲突或合作情境下的策略选择。它不仅适用于棋类游戏,更广泛应用于经济学、政治学、生物学等领域。例如,两个商家的价格战、企业间的广告投放竞争都属于博弈场景。
1.2 合作博弈的核心问题
在团队合作中,如何公平分配集体收益?假设三个朋友共同开发了一个小程序,A负责编程(贡献价值500元),B负责设计(贡献200元),C负责推广(贡献300元)。但组合后的总收益达到1200元,多出的200元该如何分配?
1.3 Shapley值的突破性贡献
诺贝尔经济学奖得主Lloyd Shapley提出:
每个成员的收益应等于其对所有可能合作子集的平均边际贡献。
以三人合作为例,计算A的Shapley值需考虑所有加入顺序的可能性(共3!=6种):
| 加入顺序 | A的边际贡献计算 | 公式表示 |
|---|---|---|
| B→C→A | 1200 - (B+C)=1200-500=700 | v({B,C,A}) - v({B,C}) |
| B→A→C | (A+B) - B = 700-200=500 | v({B,A}) - v({B}) |
| C→B→A | 1200 - (C+B)=1200-500=700 | v({C,B,A}) - v({C,B}) |
| C→A→B | (A+C) - C = 800-300=500 | v({C,A}) - v({C}) |
| A→B→C | A单独贡献=500 | v({A}) - v(∅) |
| A→C→B | 同上=500 | v({A}) - v(∅) |
最终A的Shapley值 = (700+500+700+500+500+500)/6 = 566.7元
这个计算过程体现了三个核心思想:
- 所有可能合作场景都要考虑
- 关注边际贡献而非绝对贡献
- 用排列组合保证公平性
2. Shapley值的数学表达
2.1 标准公式
ϕ i ( v ) = ∑ S ⊆ N ∖ { i } ∣ S ∣ ! ( n − ∣ S ∣ − 1 ) ! n ! [ v ( S ∪ { i } ) − v ( S ) ] \phi_i(v) = \sum_{S \subseteq N \setminus \{i\}} \frac{|S|! (n - |S| - 1)!}{n!} [v(S \cup \{i\}) - v(S)] ϕi(v)=S⊆N∖{i}∑n!∣S∣!(n−∣S∣−1)![v(S∪{i})−v(S)]
符号解析:
- v ( S ) v(S) v(S):特征子集S的预测值(如只用年龄特征的模型输出)
- n n n:特征总数(如年龄、收入、学历等8个特征)
- S S S:不包含特征i的所有可能组合(如排除"收入"特征的其他7个特征组合)
2.2 计算步骤分解
以银行风控模型(特征:年龄、收入、负债率)为例:
- 枚举所有特征排列组合(3个特征共有6种顺序)
- 计算每种顺序下各特征的边际贡献
- 如顺序为负债率→收入→年龄:
- 负债率贡献 = f(负债率) - f()(空集)
- 收入贡献 = f(负债率,收入) - f(负债率)
- 年龄贡献 = f(负债率,收入,年龄) - f(负债率,收入)
- 如顺序为负债率→收入→年龄:
- 按排列组合权重加权平均
- 每个排列组合权重 = 1/6
- 最终每个特征的Shapley值 = Σ(权重×边际贡献)
2.3 核心性质证明
SHAP满足三个黄金准则:
- 局部准确性:所有特征SHAP值之和 = 模型预测值 - 基准值
(例如:模型预测某客户违约概率80%,基准值(平均违约率)为50%,则Σφ_i=30%) - 缺失性:缺失特征的SHAP值为0
(如果某个特征完全不参与预测,其贡献必然为零) - 一致性:若特征i的边际贡献增加,则φ_i不会减少
(确保解释结果符合直观认知)
3. 案例解析:互联网广告归因难题
3.1 问题描述
某电商在三个渠道投放广告:
- A(信息流广告)
- B(开屏广告)
- C(视频广告)
单独投放效果:
| 渠道 | 转化率 |
|---|---|
| A | 10% |
| B | 30% |
| C | 5% |
组合投放效果:
| 组合方式 | 转化率 |
|---|---|
| AB | 50% |
| AC | 40% |
| BC | 35% |
| ABC | 100% |
3.2 传统方法的局限性
- 按渠道数平均分配:100%÷3≈33.3%
❌ 忽视各渠道实际贡献差异(B渠道单独转化率已是30%) - 首触点归因:假设第一个接触的渠道获得全部功劳
❌ 忽略后续渠道的促进作用
3.3 SHAP解决方案
-
枚举所有6种投放顺序
-
计算每个渠道在每种顺序下的边际贡献
投放顺序 A的贡献 B的贡献 C的贡献 A→B→C 10% 40% 50% A→C→B 10% 60% 30% B→A→C 20% 30% 50% B→C→A 65% 30% 5% C→A→B 35% 60% 5% C→B→A 65% 30% 5% -
计算平均贡献度:
- A:(10+10+20+65+35+65)/6 ≈ 34.17%
- B:(40+60+30+30+60+30)/6 = 41.67%
- C:(50+30+50+5+5+5)/6 ≈ 24.17%
3.4 结果解读
- B渠道贡献最大:即使单独投放只有30%转化率,但在组合中起到关键作用(平均提升41.67%)
- A渠道存在协同效应:当A在后期加入时(如B→A→C),其贡献度提升至20%
- C渠道局限性:后期加入时贡献急剧下降(如B→C→A顺序中仅贡献5%)
这个结果指导运营团队:
- 优先保障B渠道预算(核心驱动力)
- 在B渠道获客后追加A渠道触达(提升协同效应)
- 控制C渠道投放成本(边际效益较低)
4. SHAP与传统方法对比
| 方法 | 是否考虑特征交互 | 是否满足一致性 | 计算效率 | 适用模型类型 |
|---|---|---|---|---|
| SHAP | ✅ 全面量化交互作用 | ✅ 严格证明 | ⚠️ 高维数据较慢 | 所有模型 |
| 特征置换法 | ❌ 仅单变量影响 | ❌ 可能矛盾 | ✅ 高效 | 所有模型 |
| 部分依赖图 | ❌ 忽略交互作用 | ❌ 可能误导 | ✅ 高效 | 所有模型 |
| 线性模型系数 | ❌ 仅线性关系 | ✅ 限线性模型 | ✅ 高效 | 线性模型 |
通过博弈论的严谨框架,SHAP解决了传统方法存在的"贡献分配不公"、"忽略特征交互"等痛点,成为当前最可靠的模型解释工具之一。
三、SHAP实践全流程指南
1. 环境准备与数据加载
1.1 安装SHAP包
首先需要安装SHAP的Python包,推荐使用pip安装最新版本:
pip install shap
1.2 数据准备与模型训练
以经典的加州房价预测数据集为例:
数据集的特征(X)包含以下 8 个变量:
- MedInc:街区组中的收入中位数(单位:千美元)
- HouseAge:街区组中房屋的中位年龄(单位:年)
- AveRooms:每个房屋的平均房间数
- AveBedrms:每个房屋的平均卧室数
- Population:街区组的人口总数
- AveOccup:每个家庭的平均居住人数
- Latitude:街区组的纬度坐标
- Longitude:街区组的经度坐标
目标变量(y)是 房屋价格的中位数的自然对数
import shap
from sklearn.model_selection import train_test_split
from xgboost import XGBRegressor
# 加载数据集
X, y = shap.datasets.california()
# 拆分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 打印部分数据(前5行)
print("X_train sample:")
print(X_train.head())
print("\ny_train sample:")
print(y_train[:5])
# 确保 X_train 是 pandas.DataFrame
import pandas as pd
if not isinstance(X_train, pd.DataFrame):
X_train = pd.DataFrame(X_train)
# 训练模型
model = XGBRegressor().fit(X_train, y_train)
2. Explainer选择与实例化
2.1 Explainer类型全解析
根据模型类型选择合适的Explainer,这是影响计算效率和解释精度的关键步骤:
| Explainer类型 | 适用模型 | 计算效率 | 特殊优势 |
|---|---|---|---|
| TreeExplainer | 树模型(XGBoost/LightGBM) | ⭐⭐⭐⭐ | 精确计算,支持特征交互 |
| DeepExplainer | 深度学习模型 | ⭐⭐ | 基于DeepLIFT算法 |
| KernelExplainer | 通用模型(黑箱模型) | ⭐ | 无需模型结构信息 |
| LinearExplainer | 线性模型 | ⭐⭐⭐⭐⭐ | 解析解直接计算 |
代码示例:
# 创建解释器并显式传入特征名称
explainer = shap.TreeExplainer(model, feature_names=X_train.columns.tolist())
shap_values = explainer.shap_values(X_train)
shap.summary_plot(shap_values, X_train)

图表解读:
-
图中每个点的含义
- 点的位置:每个点代表一个样本(数据行)的某个特征值对应的 SHAP 值(即该特征对模型预测的贡献)
- 颜色深浅:颜色表示特征值的大小(红色表示高值,蓝色表示低值),帮助观察特征值与影响的关联趋势
- 横轴(X 轴):表示 SHAP 值的大小,即特征对模型预测的贡献程度(正值推动预测增大,负值减小)
- 纵轴(Y 轴):按特征排序显示,通常按全局重要性从上到下排列
-
如何判断特征重要性
- 特征位置:纵轴越靠上的特征,全局重要性越高
- 点的分布范围:横轴上某特征的点分布越分散,说明其影响波动越大,重要性越高
-
如何分析特征影响方向
- 正/负 SHAP 值:正值推动预测结果增大(如房间数越多房价越高),负值减小
- 颜色趋势:红色点集中在 SHAP 正值区域,说明高特征值推动预测值升高
2.2 Explainer参数优化
对于KernelExplainer需要特别注意:
link参数:默认使用logit链接函数(分类任务),回归任务应设置为"identity"nsamples:采样次数影响精度与速度,推荐首次尝试100-200次
3. SHAP值计算详解
3.1 核心计算步骤
# 计算SHAP值(对TreeExplainer而言)
shap_values = explainer.shap_values(X_test)
# 计算特征交互作用(需额外消耗约30%时间)
shap_interaction_values = explainer.shap_interaction_values(X_test)
3.2 计算过程剖析
- 基准值确定:
explainer.expected_value即训练集预测值的均值 - 边际贡献计算:遍历所有特征排列组合,计算每个特征加入时的预测值变化
- 权重分配:根据特征位置对边际贡献加权平均
⚠️ 注意:深度学习模型计算可能需要GPU加速,建议使用
tf.config.experimental.set_memory_growth控制显存分配
4. 可视化分析全流程
4.1 单样本解释:瀑布图与力图
# 瀑布图(显示第一个测试样本的解释)
shap.plots.waterfall(explainer.expected_value, shap_values[0])
# 力图(支持交互式HTML展示)
shap.plots.force(explainer.expected_value, shap_values[0], X_test.iloc[0])

瀑布图功能:
- 展示单个样本的特征贡献
- 红色条形向右推(增加预测值),蓝色条形向左推(减少预测值)
- 特征按贡献大小排序(顶部为影响最大的特征)
力图功能:
- 交互式展示特征影响
- 动态显示特征如何推动预测值从基线值变化到最终结果
- 支持多样本对比
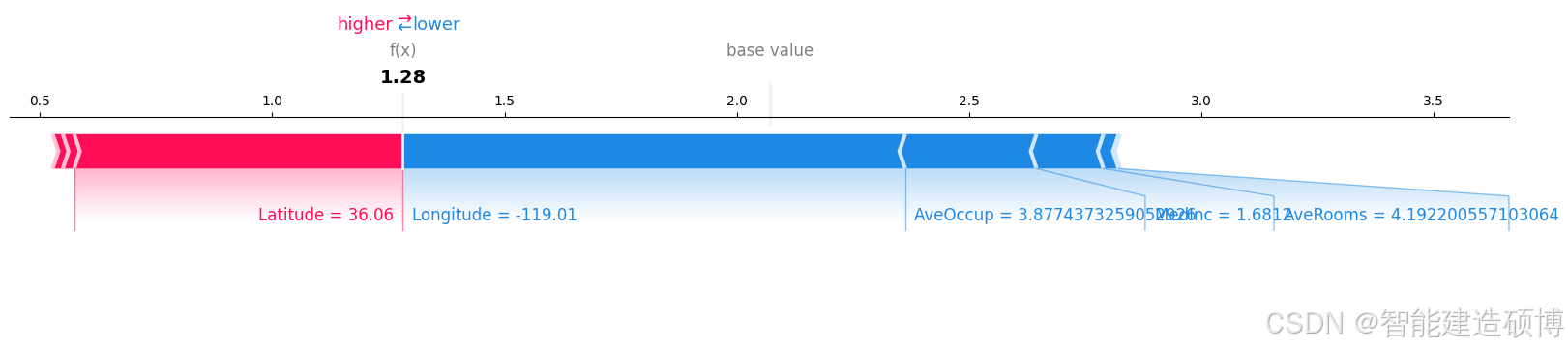
解读方法:
- 从基线值开始(全局平均预测值)
- 观察特征条形方向:红色向右推(如 MedInc 高收入增加房价)
- 叠加贡献得到预测值:最终预测值 = 基线值 + 所有特征贡献总和
4.2 全局特征分析:摘要图进阶
# 绘制特征重要性条形图
shap.summary_plot(
shap_values,
X_test,
feature_names=X_train.columns.tolist(),
plot_type="bar",
max_display=10
)

4.3 特征交互分析
# 使用加州数据集的特征(如 MedInc)
shap.dependence_plot("MedInc", shap_values, X_test, interaction_index="AveRooms")

解读要点:
- 非线性趋势:点云呈现U型或分段聚集说明主特征与目标变量存在复杂关系
- 交互效应:红色点(高交互特征值)集中在SHAP值某一侧说明两特征强关联
4.4 其他高级可视化
# 决策图(显示特征对决策路径的影响)
shap.decision_plot(explainer.expected_value, shap_values[0], X_test.iloc[0])

# 热力图(分析特征共线性)
shap.plots.heatmap(shap_values, instance_order=shap_values)



























 494
494

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










