斯坦福算法博弈论二十讲 - 第三章迈尔森引理

最新推荐文章于 2024-09-06 10:38:06 发布

RivaJ

最新推荐文章于 2024-09-06 10:38:06 发布

阅读量792

点赞数 25

分类专栏：斯坦福算法博弈论二十讲文章标签：算法

本文链接：https://blog.csdn.net/RivaJ/article/details/140089227

版权

斯坦福算法博弈论二十讲专栏收录该内容

3 篇文章 0 订阅

订阅专栏

这章似乎开始进行数学抽象了

单参数环境 在单参数环境中，有 $n$ 个智能体，每个智能体 $i$ 都对单个物品有非负的估值，此估值为私人信息，记作 $v_i$ 。最后，有一个可行集 $X$ 。 $X$ 中的每个元素 $x$ 都是 $n$ 维向量 $(x_1, x_2, \cdots, x_n)$ ，其中 $x_i$ 表示智能体 $i$ 获得的物品数量。

（单参数环境为什么叫单参数环境呢，查了些资料，感觉比较贴合语境的说法如下: 一种简化的博弈环境，其中所有参与者的策略选择只依赖于一个关键参数或变量，如这里对物品的估值。到现在为止还是没感出本书侧重是算法还是博弈论TT，再次吐槽概念的引入毫无铺垫，越发像是本讲义了）

（ $n$ 维向量 $x$ 是某种可能的分配方案，可行集 $X$ 可理解为所有可能的分配方案的集合)，下面是几个例子：

单物品拍卖 可行集 $X$ 是满足 $\sum_{i=1}^n \le 1$ （总分配量不超过1）的0-1向量 $x$ 所组成的集合，
k物品拍卖 有 $k$ 个相同物品进行拍卖，并且每个竞拍者最多获得其中一个。那么可行集 $X$ 就是满足 $\sum_{i=1}^n \le k$ （总分配量不超过 $k$ ）的0-1向量 $x$ 所组成的集合
关键字搜索拍卖 一个竞拍者最多获得一个广告位，并且一个广告位最多分配给一个竞拍者，如果竞拍者 $i$ 得到了广告为 $j$ ，那么 $x$ 的 $i$ 分量就等于其获得的广告位的点击率 $\alpha_j$ 。（我的第一直觉这种情况下， $x$ 应该是广告位的一个排列组合，不过显然用点击率来代表 $x$ 的分量给未来分析计算会带来很大的方便）
公共项目决策 决定是否修建一个供所有人共享的公共项目，比如一座桥。其可以被建模为可行集 $X=\{(0,0,\cdots,0), (1,1,\cdots,1)\}$ （建了就是给所有人分配了，不建就所有人都不分配）

二价拍卖需要完成以下步骤：

收集所有智能体的出价 $\vec b=(b_1,\cdots, b_n)$ ，称为出价向量或出价组合
【分配规则】选择一个可行的分配 $\vec {\phantom{b}x}(\vec b)\in X\subseteq \mathbb{R}^n$
【支付规则】选择一个支付 $\vec{\phantom{b}p}(\vec b)\in X\subseteq \mathbb{R}^n$

直接显示机制（direct-revelation mechanism） 机制要求智能体直接地显露其私人估值，如二价拍卖；对应的，非直接显示机制，如迭代升价拍卖

如果收益函数是拟线性的（quasilinear），则智能体 $i$ 的收益函数如下：

$u_i(\vec b)=v_i\cdot x_i(\vec b) - p_i(\vec b)$ (私人估值 * 分配个数 - 支付)

其中，支付规则应满足： $p_i(\vec b)\in [0, b_i\cdot x_i(\vec b)]$ （显然需要保证支付不为负，不太显然的是要保证真实报价的收益不为负）

定义3.5 可实施的分配规则 对于一个单参数环境，对于一个分配规则 $\vec x$ ，如果存在一个支付规则 $\vec p$ 使得直接显示机制 $(\vec x, \vec p)$ 是DSIC的，则称这个分配规则 $\vec x$ 是可实施的。

定义3.6 单调分配规则 如果对于每个智能体 $i$ 和所有其他智能体的出价向量 $\vec b_{-i}$ ，对智能体 $i$ 的分配函数 $x_i(z, \vec b_{-i})$ 是 $i$ 的出价 $z$ 的单调非减函数，那么就称分配规则 $\vec x$ 是单调的。（显然，出价越高，赢得的物品越多）

定理3.7 迈尔森引理 在一个单参数环境下：

一个分配规则 $\vec x$ 是可实施的，当且仅当它是单调的（说明定义3.5和3.6是等价的）
如果 $\vec x$ 是单调的，那么存在唯一的支付规则，使得直接显示机制 $(\vec x, \vec p)$ 是DSIC的，且使得对于所有报价 $b_i=0$ 均有 $p_i(\vec b) = 0$ （唯一的支付规则，还是挺惊讶的）
支付规则有明确的表达式

迈尔森引理的证明

part1 可实施等价于单调

$\vec x$ 是可实施的 $\Leftrightarrow$ 存在 $\vec p$ 使得 $(\vec x, \vec p)$ 是DSIC的。

$\Leftrightarrow$ 对于任意的 $0 \le y < z$ ，必有（请想象两智能体，其中一个的估值是 $y$ ，则有式1，另一个的估值是 $z$ 则有式2：

$\left\{\begin{matrix} y\cdot x(y) - p(y) \ge y\cdot x(z) - p(z) \\ z\cdot x(z) - p(z) \ge z\cdot x(y) - p(y) \end{matrix}\right.$

$\Leftrightarrow$ $z\cdot (x(y) - x(z))\le p(y)-p(z)\le y\cdot(x(y) - x(z)) \quad (3.4)$

$\Leftrightarrow x(y) - x(z) \le 0$

$\Leftrightarrow$ $\vec x$ 是单调的。（注意证明过程中 $p$ 的任意性和存在性的转变，理解了好久才想明白）

part2 支付规则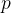 $p$ 的唯一性和表达式

观察式(3.4)，令 $z = y + \mathrm{d}y$ ，则有

$(y+\mathrm dy)\cdot (x(y) - x(y + \mathrm dy))\le p(y)-p(y+\mathrm dy)\le y\cdot(x(y) - x(y+\mathrm dy))$

$\Rightarrow -(y+\mathrm dy)\frac{\mathrm dx(y)}{\mathrm dy}\le \frac{-\mathrm dp(y)}{\mathrm dy} \le -y\cdot \frac{\mathrm dx(y)}{\mathrm dy}$

$\Rightarrow yx'(y) \le p'(y) \le yx'(y) + \mathrm d y x'(y)$

$\Rightarrow p'(z) = zx'(z)$ （揭示了 $p$ 在 $z\phantom{[}$ 处的变化 = $z\cdot$ [ $x$ 在 $z$ 处的变化] ）

$\Rightarrow \left\{\begin{matrix} p_i(b_i, \vec b_{-i}) = \sum_{j=1}^l z_j\cdot [x_i(\cdot, b_{-i})\text{diff at }z_j] \quad (3.5)\\ p_i(b_i, \vec b_{-i})=\int_0^{b_i}z\cdot\frac{\mathrm d}{\mathrm dz}x_i(z, \vec b_{-i})\mathrm dz \quad (3.6) \end{matrix}\right.$

（最后两步不是很严谨，不过总算强行讲书中列出的。想了两天才得到勉强能让自己接受的证明过程，原书的证明过程实在有点难理解。如果有看到严谨地数学证明过程，烦请在评论区提供出处）

支付公式的运用

根据式3.5，可以分析【二价拍卖】和【关键字搜索拍卖】（前者比较简单，不复述，后者如下，其也是对练习2.3的解答

题设：有 $k$ 个广告位，点击率分别为 $\alpha_1\ge\alpha_2\ge\cdots\alpha_k$ 。 $\vec x(\vec b)$ 表示分配规则，对于所有 $i=1,2,\cdots,k$ ，将质量第 $i$ 好的广告位分配给出价第 $i$ 高的竞拍者。这个分配规则是单调的。因此迈尔森支付公式（3.5）可以给出唯一的支付规则 $\vec p$ ，使得机制 $(\vec x, \vec p)$ 是DSIC的。考虑一个报价向量 $\vec b$ ，对所有报价从高到底排序有 $b_1\ge b_2\ge\cdots\ge b_n$ 。考虑竞拍者 $i$ 在第 $i$ 个广告位上的单位点击量支付：

$p_i(\vec b) = \sum_{j=1}^l z_j\cdot [x_i(\cdot, b_{-i})\text{diff at }z_j] \quad (3.5)$

竞拍者 $i$ 的分配突变在 $b_k, \cdots, b_i$ 之间，每个diff为 $\alpha_j - \alpha_{j + 1}$ ，因此

$p_i(\vec b) = \sum_{j = i}^k b_{j+1}\frac{\alpha_j-\alpha_{j+1}}{\alpha_i}$ （感觉不是那么显然的，经济学的书大多有这个毛病）

据此，每当一个竞拍者的链接被点击，实际上他需要支付的数额是比他低的其他报价的一个凸组合（已经忘记凸组合是个啥定义了，反正是个组合就对了）。

在做练习2.3时，凭直觉给出了错误的答案，同样是将第 $i$ 好的广告位分配给第 $i$ 高的报价者，但是收取第 $i+1$ 高的报价。事实上这个答案虽然不是DSIC的，但是误打误撞，是现实中搜索引擎常用的方式，被称为“广义二价”（GSP）拍卖（显然GSP的支付更高）。

GSP拍卖在某种意义上和DSIC的拍卖机制是等效的（Interesting！）

练习3.1~3.3 略（已经证明了原命题，何必费那个劲去证明逆否命题）

练习3.4 （感觉要学到第7章才能正确回答这个问题，因为对于一个竞拍者，除了有私人估值，还有一个公开的质量，这都有两个参数了，而前面都是单参数的）简单尝试一下吧：

首先假设所有人都真实报价， $\vec b = [v_1, v_2, \cdots, v_n]$

不妨假设竞拍者 $j$ 获得广告位 $j$ ，则社会福利为 $\sum_{j=1}^k v_j\beta_j\alpha_j$ 在满足 $v_1\beta_1\ge v_2\beta_2\ge\cdots \ge v_k\beta_k$ 最大。

因此针对任意报价 $\vec b = [b_1, b_2, \cdots, b_n]$ ，我们按 $b_i\beta_i$ 从高到低的顺序分配广告位。

显然这个分配规则是单调的，可以根据公式3.5，得到唯一使得机制为DSIC的支付规则。

假设 $b_1\beta_1\ge b_2\beta_2\ge\cdots\ge b_n\beta_n$ ，竞拍者 $i$ 的到广告位 $i$ ，

分配函数突变的位置： $[b_k\beta_k, \cdots , b_2\beta_2, b_1\beta_1]$ ，分配的突变量为： $[\beta_k\alpha_k, \beta_{k-1}\alpha_{k-1} - \beta_k\alpha_k ,\cdots , \beta_1\alpha_1 - \beta_2\alpha_2]$