【MWORKS专业工具箱系列教程】控制系列工具箱第七期：PID控制器设计

已于 2024-12-18 16:17:51 修改
阅读量1.4k 收藏 28
点赞数 19
分类专栏： 控制系列工具箱 文章标签： 建模仿真 控制系统 pid控制
于 2024-10-12 09:25:32 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/SZ_TONGYUAN/article/details/142811751
版权

本工具箱教程以控制系统模型创建、分析与设计流程为主线，通过大量示例介绍MWORKS控制系统工具箱的功能和具体使用。共计10篇文章，上一篇主要介绍了控制系统根轨迹分析。

同元软控：【MWORKS专业工具箱系列教程】控制系列工具箱第六期：根轨迹分析

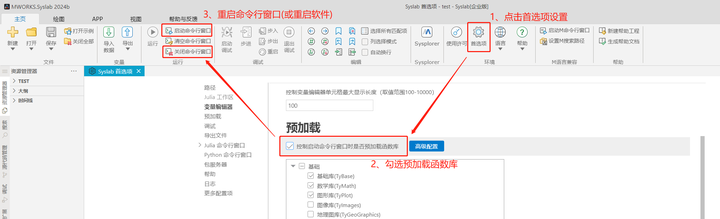
本教程代码均可直接复制到Syslab中运行，使用教程中代码前需参照下述方法加载函数库内容： 方法一：在Syslab的命令行窗口先后输入using TyControlSystems和using TyPlot并回车(重启软件或命令行窗口后需重新输入)； 方法二：按照下图中的方法预加载函数库(设置好后每次启动软件默认加载)。

第七期：PID控制器设计

一、PID控制在工业界的应用

在当今应用的工业控制器中，有半数以上采用了PID或变形PID控制器。PID控制的价值取决于它们对大多数控制系统的广泛适用性，体现在：

  1. 原理简单，应用方便，参数整定灵活

  2. 适用性强，特别是当被控对象的数学模型未知，而不能使用解析设计方法时，PID控制就显得特别有用

  3. 鲁棒性强，控制品质对受控对象的变化不太敏感，如受控对象受外界扰动时，无需经常改变控制器参数或结构

国际自动控制联合会（IFAC）每三年召开一次的世界大会是自动控制领域的顶级学术会议

IFAC

IFAC · International Federation of Automatic Control​icon-default.png?t=O83Ahttp://www.ifac-control.org/

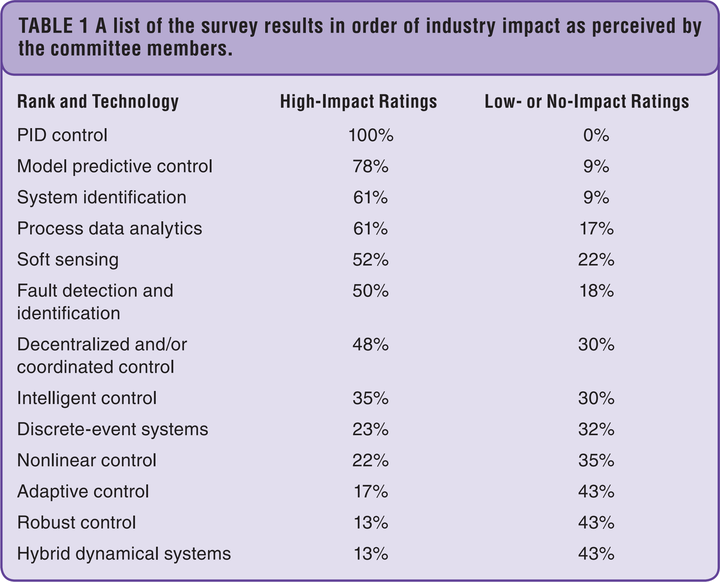
IFAC在2014年发布的一项调查报告（链接：A Survey on Industry Impact and Challenges Thereof，Tariq Samad）显示，PID控制在当时仍然是在工业领域具有最大影响力的控制技术。

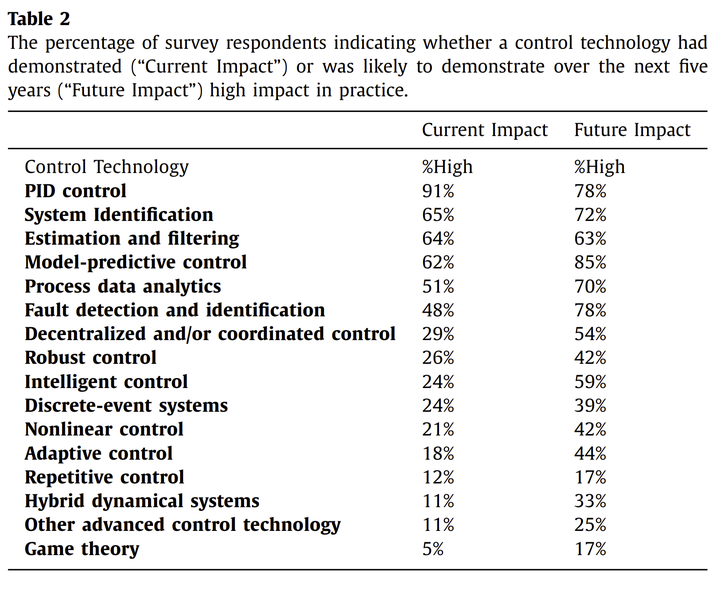
A Survey on Industry Impact and Challenges Thereof，Tariq Samad

2020年在Annual Reviews in Control中发表的 Industry engagement with control research: Perspective and messages ，表明PID控制的当前影响力仍然最高，且在未来5年内可能是工业实践中影响力较高的控制技术，紧随其后的则是MPC技术。

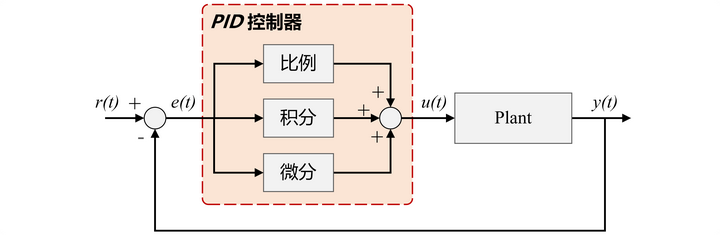
Industry engagement with control research: Perspective and messages

二、PID控制器基本结构与Syslab中pid函数

PID控制器基本结构

PID控制框图
最低0.47元/天 解锁文章
【MWORKS专业工具箱系列教程】控制系列工具箱第十期：非线性系统线性化
SZ_TONGYUAN的博客
12-18 1410
本工具箱教程以控制系统模型创建、分析与设计流程为主线，通过大量示例介绍MWORKS控制系统工具箱的功能和具体使用。共计10篇文章，上一篇主要介绍了状态反馈设计。本教程代码均可直接复制到Syslab中运行，使用教程中代码前需参照下述方法加载函数库内容： 方法一：在Syslab的命令行窗口先后输入using TyControlSystems、using TyPlot和using TyBase并回车(重启软件或命令行窗口后需重新输入)；方法二：按照下图中的方法预加载函数库(设置好后每次启动软件默认加载)。
【MWORKS专业工具箱系列教程】控制系列工具箱第一期：控制系统模型创建
SZ_TONGYUAN的博客
09-19 4051
支持将控制系统的构成环节指定为传递函数、状态空间或零极点增益模型，通过函数和应用程序，可实现对系统时域和频域响应的分析与可视化。MWORKS控制系列工具箱包括基础控制系统工具箱、基于模型的控制器设计工具箱、系统辨识工具箱、鲁棒控制工具箱等，其中基础控制系统工具箱与基于模型的控制器设计工具箱是MWORKS控制系列工具箱的基础，下文将这两个工具箱合称为控制系统工具箱。考虑如果传递函数分子分母多项式给出的不是完全展开的形式，而是若干因式的乘积，或者包括其他运算。系统模型的一种表述形式为：传递函数矩阵。
【MWORKS专业工具箱系列教程】控制系列工具箱第八期：交互式控制系统设计APP
SZ_TONGYUAN的博客
12-18 1419
经典控制理论有两大核心设计方法，分别是频率响应法和根轨迹法。控制系统设计器APP让用户可以使用交互式的波特图编辑器、根轨迹编辑器来添加、修改和删除控制器的极点、零点和增益，从而实现基于这两大方法的控制器设计和分析。控制系统设计器APP支持用户自定义绘制阶跃、脉冲、波特、奈奎斯特及尼克尔斯图，通过交互式对话框的方式实现对控制器的设计，并且各绘图窗口会实时进行更新重绘，将控制器效果进行直观展示。相比传统的代码实现方式大大减少了计算、编程及后处理等所需要的时间。
全网首发 | 科学计算与系统建模仿真系列课程上线啦！
SZ_TONGYUAN的博客
08-16 838
MWORKS从入门到精通~
电脑鼠原理学习笔记
m0_64411232的博客
04-29 2514
2022/4/28 电脑鼠执行控制需求 速度要求：最大搜索速度120cmc/s 最大冲刺速度：220cm/s 纵横位置误差+-3.4cm/s 控制电脑鼠走在中间 PID闭环控制 控制器性能要求：稳、快、准 比例系数P： 可以加快调节速度，减小稳态误差，当过大时可能会导致振动次数增加 积分系数I ： 通过调节可以消除稳态误差，提高控制的精度。 微分系数P： 调节可以减少超调量，增加系统的稳定性。 按照Kp，Ki，Kd的顺序，从零调整参数： 增大比例增益Kp，达到期望稳定速度后； 增
电脑鼠模糊PID控制算法研究
01-29
电脑鼠模糊PID控制算法研究，很好的电脑鼠资料，适合学习PID等一系列学习。
microMouse迷宫电脑鼠完整pcb设计文件,包含原理图和pcb
01-06
microMouse--迷宫电脑鼠完整pcb设计文件,基于Altium designer制作，包含原理图和pcb。
电脑鼠 | 增量式PID
qq_40316114的博客
09-09 608
//以下为电脑鼠程序中电脑鼠直行的增量式PID控制 //error=e(k); d_error=e(k)-e(k-1); dd_error=e(k)-2e(k-1)+e(k-2); // __GmSPID.sFeedBack: 编码器反馈的速度值； //__GmSPID.sRef: 直行速度的期望值； //deadband: 误差死区，允许的误差范围； //error_IMAX: ???...
【MWORKS专业工具箱系列教程】控制系列工具箱第六期：根轨迹分析
SZ_TONGYUAN的博客
10-11 1993
从控制设计的角度来看，在某些系统中，简单的增益调整可将闭环极点移动到需要的位置，这种情况是将设计问题转变为选择合适的增益值问题。但是，如果仅仅靠增益调整得不到满意的效果，则需要在系统中增加校正器，通过校正器的作用，将闭环极点移动到需要的位置，当然，各类时域响应指标都能决定闭环极点在复频域的可配置区域，当一个系统需要满足多个指标，那么各指标对应可配置区域的交集就是可以同时满足所有指标的闭环极点可配置区域。系统的瞬态响应类型由闭环极点确定，一阶系统简单，其总是稳定的、无震荡、响应单调；
【MWORKS专业工具箱系列教程】控制系列工具箱第九期：状态反馈设计
SZ_TONGYUAN的博客
12-17 1292
本篇主要介绍了状态空间设计——极点配置方法，以及基于极点配置法的型伺服系统设计
【MWORKS专业工具箱系列教程】控制系列工具箱第四期：时域分析
SZ_TONGYUAN的博客
09-29 2572
单位脉冲信号是一个持续时间为∆的的短脉冲，对于任意的∆值，其面积均为1，随着∆→0，𝛿Δ(𝑡)变得越来越窄，越来越高，但单位面积不变。t为标量：计算[0,t]内的响应，t为向量，计算各点的阶跃响应。t为标量：计算[0,t]内的响应，t为向量，计算各点的脉冲响应。计算任意信号响应数据，y 为响应数据数组，t 为时间向量，x 为状态数组。计算并直接返回系统阶跃响应图。计算阶跃响应数据，y 为响应数据数组，t 为时间向量，x 为状态数组。计算阶跃响应数据，y 为响应数据数组，t 为时间向量，x 为状态数组。
【数据分析与科学计算】Anaconda安装与环境管理教程：Python数据科学平台快速入门指南
05-21
内容概要：本文档详细介绍了Anaconda的安装、环境管理和包管理的方法。Anaconda是一个强大的Python数据科学平台，提供了包管理器和环境管理器。安装部分包括了从官网或国内镜像源下载并安装Anaconda，安装时建议修改安装路径并勾选添加环境变量。环境管理方面，涵盖了创建、激活、退出、查看和删除虚拟环境的具体命令。包管理则讲解了在虚拟环境中安装、卸载以及查看已安装包的操作。此外，还提供了配置国内镜像源以提高下载速度的方法，以及一些常用命令与技巧，如更新所有包、导出环境和从配置文件创建环境等。; 适合人群：对Python数据科学感兴趣的初学者，以及需要使用Anaconda进行环境和包管理的开发者。; 使用场景及目标：①帮助用户快速完成Anaconda的安装；②让用户掌握虚拟环境的创建与管理，确保不同项目之间的依赖隔离；③使用户能够熟练地进行包的安装、卸载和更新操作；④提高用户在国内网络环境下获取资源的速度。; 阅读建议：阅读时可结合自身需求重点学习环境管理和包管理的相关命令，对于配置镜像源的内容，可根据自己的网络情况选择是否配置。
计算机图形学实验一（基本图形生成（一））
05-21
基于visualstudio2010，包括所有源代码，可以运行， 编程实现直线的 DDA 算法及 Bresenham 算法绘制任意斜率的直线。 设计一个图形并调用 1 中的 Bresenham 算法程序绘制。
3D空间避障与路径规划：RRT与RRT算法的MATLAB实现及应用 3D建模 基于RRT和RRT算法的3D场景路径规划与障碍物距离分析
05-21
内容概要：本文详细介绍了RRT（快速随机树）和RRT*算法在3D场景下的应用，重点在于如何绕过两个圆柱障碍物到达目标点。文中通过MATLAB代码实现了路径规划的具体步骤，包括初始化参数、随机采样、寻找最近节点、扩展树结构、判断是否绕过障碍物以及输出路径图和路径点与障碍物最小距离变化图。此外，还对算法进行了简要介绍，指出了其优点和局限性。 适合人群：从事机器人技术、自动化控制、机械臂路径规划的研究人员和技术人员，尤其是对3D空间避障与路径规划感兴趣的开发者。 使用场景及目标：①帮助研究人员理解和实现RRT和RRT*算法在3D环境中的具体应用；②为移动机器人和机械臂的路径规划提供理论支持和实践指导；③通过图示和代码示例，使读者能够更好地掌握算法的实现细节。 其他说明：虽然RRT和RRT*算法在处理复杂环境下的路径规划问题时表现出色，但也存在一些局限性，如可能陷入局部最优解等问题。未来可以通过改进算法来提升其性能和适用性。
科普内容创作者科普文章AI写作提示词科普论文写作提示词（AI提示词Prompt）
05-21
科普内容创作者科普文章AI写作提示词科普论文写作提示词（AI提示词Prompt）
一种新型具有多陷波特性的超宽带天线.zip
最新发布
05-21
一种新型具有多陷波特性的超宽带天线.zip
cmd-bat-批处理-脚本-vcvars32.zip
05-21
cmd-bat-批处理-脚本-vcvars32.zip
模块化SOC主动均衡模型：六节电池串联系统的充放电均衡解决方案 电池管理系统
05-21
内容概要：本文介绍了一种专为六节电池串联设计的模块化SOC主动均衡模型。该模型采用底层双向反激变换器和顶层buck-boost均衡的双重策略，旨在解决电池组中各节电池SOC不一致的问题。通过模块化设计，模型实现了灵活性和扩展性，适用于不同类型的电池组。文章详细介绍了模型的工作原理、设计思路以及仿真实验结果，验证了模型的有效性。 适合人群：从事电池管理系统的研发人员、电力电子工程师、科研工作者。 使用场景及目标：①研究电池组充放电均衡技术；②优化电池管理系统的设计；③作为论文创新和仿真实验的基础。 阅读建议：重点理解双向反激变换器和buck-boost均衡的具体实现方法及其协同工作的机制，结合仿真实验数据进一步验证模型效果。
cmd-bat-批处理-脚本-LaunchDevCmd.zip
05-21
cmd-bat-批处理-脚本-LaunchDevCmd.zip
用mworks搭建球杆系统
12-29
### 使用 MWorks 搭建倒立摆控制系统 #### 加载必要的函数库 为了使用 MWorks 的控制系统工具箱来搭建倒立摆控制系统，首先需要加载所需的函数库。可以通过两种方式完成这一操作： - **方法一**：在 Syslab 命令行窗口依次输入 `using TyControlSystems`、`using TyPlot` 和 `using TyBase` 并按回车键执行[^1]。 - **方法二**：通过图形界面配置预加载项，使得每次启动软件时自动加载这些库。这一步骤可以减少重复劳动，提高工作效率。 #### 创建倒立摆系统的数学模型 接下来，在 MWorks 中定义倒立摆的动力学方程。通常情况下，倒立摆系统可以用一组微分方程表示其运动特性。这里提供了一个简单的线性化状态空间表达式的例子： ```matlab A = [0 1; g/l, 0]; % 状态矩阵 A (假设重力加速度g=9.8m/s², 杆长l) B = [0; 1/m*l^2]; % 输入矩阵 B (质量 m) C = eye(2); % 输出矩阵 C D = zeros(2,1); % 直接传递矩阵 D sys = ss(A,B,C,D); ``` 上述代码片段创建了一个连续时间的状态空间对象 `sys` 表示简化后的单级倒立摆模型。 #### 设计控制器 对于这样一个不稳定的过程，PID 控制器是一个常见的选择。下面展示如何利用 MWorks 提供的功能快速构建 PID 调节器并与之前建立的植物模型连接起来形成闭环结构： ```matlab Kp = 10; Ki = 5; Kd = 2; pidController = pid(Kp,Ki,Kd); cl_sys = feedback(sys*pidController,1); ``` 这段脚本实现了比例积分微分控制算法的设计，并将其应用于已有的物理过程之上，从而构成了完整的反馈环路体系。 #### 进行仿真实验 最后，借助于内置的时间响应分析功能测试所设计好的控制系统性能。比如绘制阶跃响应曲线可以帮助评估稳定性以及动态品质指标如上升时间和超调量等参数特征： ```matlab step(cl_sys); title('Step Response of Inverted Pendulum Control System'); grid on; ``` 以上就是基于 MWorks 工具集实现简单版球杆（即所谓的“倒立摆”）稳定化的全过程概述。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值