【MWORKS专业工具箱系列教程】控制系列工具箱第六期：根轨迹分析

本工具箱教程以控制系统模型创建、分析与设计流程为主线，通过大量示例介绍MWORKS控制系统工具箱的功能和具体使用。共计10篇文章，上一篇主要介绍了控制系统频域分析。

同元软控：【MWORKS专业工具箱系列教程】控制系列工具箱第五期：频域分析

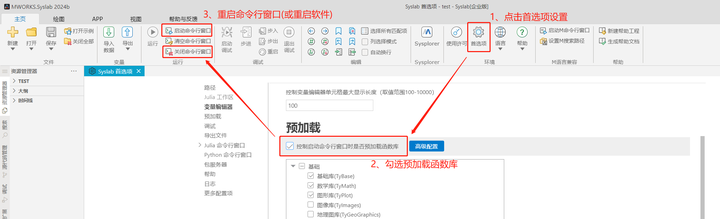
本教程代码均可直接复制到Syslab中运行，使用教程中代码前需参照下述方法加载函数库内容： 方法一：在Syslab的命令行窗口先后输入using TyControlSystems和using TyPlot并回车(重启软件或命令行窗口后需重新输入)； 方法二：按照下图中的方法预加载函数库(设置好后每次启动软件默认加载)。

---

第六期：根轨迹分析

一、什么是根轨迹？

根轨迹是当系统的某个参数从 变化到 时，闭环特征方程的根在 平面上的变化轨迹。

具有可变参数K的闭环控制系统，这里K为系统开环增益

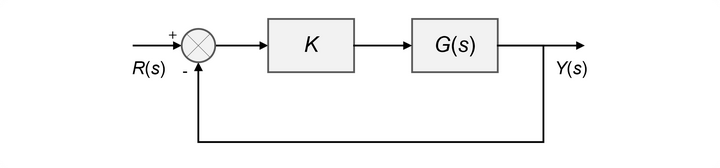
如上图所示简单的单回路系统，其闭环表达式为：

其特征方程为：

其中， 为可变参数，且满足  。随着 的变化，闭环特征方程的根在  平面的轨迹即为系统根轨迹。

二、基于根轨迹法的控制系统设计思路

根轨迹法是经典控制理论的两大核心设计方法之一（另一为频率响应法）

闭环系统瞬态响应的基本特性与闭环特征根（闭环极点）的位置紧密相关。如果系统具有可变的回路增益，则闭环极点的位置取决于所选择的回路增益值。因此，当回路增益变化时，掌握闭环极点在 平面如何移动，对设计控制系统来说很重要。

从控制设计的角度来看，在某些系统中，简单的增益调整可将闭环极点移动到需要的位置，这种情况是将设计问题转变为选择合适的增益值问题。但是，如果仅仅靠增益调整得不到满意的效果，则需要在系统中增加校正器，通过校正器的作用，将闭环极点移动到需要的位置，这部分内容将在本系列第八期：交互式控制系统设计App中进行详细讨论，敬请持续关注。

以上是基于根轨迹法设计控制系统的基本思路。根轨迹法指出了开环极点和零点应当怎样变化才能使系统的响应满足系统的性能指标，特别适合于迅速地获取近似结果。

三、用Syslab绘制根轨迹图

求解三阶以上的特征方程根异常麻烦，Syslab则为该问题提供了一个简便的解法，通过 rlocus 函数即可轻松绘制。

但是，手工方法绘制根轨迹的经验、基本规则，对于理解根轨迹以及通过交互方式设计控制系统都至关重要。

比如&