[IEEE TPAMI 2024]Robust Visual Question Answering: Datasets, Methods, and Future Challenges

最新推荐文章于 2025-04-24 20:30:00 发布

夏莉莉iy

最新推荐文章于 2025-04-24 20:30:00 发布

阅读量1k

点赞数 38

分类专栏：综述笔记文章标签：人工智能深度学习 transformer 计算机视觉神经网络语言模型机器学习

本文链接：https://blog.csdn.net/Sherlily/article/details/147372566

版权

综述笔记专栏收录该内容

20 篇文章

订阅专栏

论文网址：Robust Visual Question Answering: Datasets, Methods, and Future Challenges | IEEE Journals & Magazine | IEEE Xplore

英文是纯手打的！论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误，若有发现欢迎评论指正！文章偏向于笔记，谨慎食用

2.3.1. Task Formulation

2.3.2. VQA Paradigm

2.4. Datasets

2.4.1. In-Distribution Setting

2.4.2. Out-of-Distribution Setting

2.5. Evaluations

2.6. Debiasing Methods

2.6.1. Ensemble Learning

2.6.2. Data Augmentation

2.6.3. Self-Supervised Contrastive Learning

2.6.4. Answer Re-Ranking

2.7. Exploring the Robustness of Vision-Language Models for VQA

2.8. Discussions and Future Directions

2.9. Conclusion

3. Reference

1. 心得

（1）宝贝你都TPAMI了我还有什么理由不看呢

（2）介绍了对学习到偏差/某个固定分布问题，数据集和模型各自的解决办法

（3）可以说总结概括都还ok但不是那种一眼惊艳的文章（人总是对TPAMI有额外的期望

2. 论文逐段精读

2.1. Abstract

①Existing visual question answering (VQA) methods is lack of generalization

2.2. Introduction

①Significance of VQA: image retrieval, intelligent virtual assistants, visual recommendation systems, autonomous driving（啊这样的吗？？）

②Methods of VQA: joint embedding, attention mechanism, and external knowledge

③In distribution (ID) performance and out of distribution (OOD) performance:

（作者意思是在某个数据集里面Q是问what sports且非常多个问what sports的回答A都是tennis因此机器认为这俩东西挂钩了导致别的运动也会被回答为tennis）（这个就是学习到了偏见，是很常见的问题）

2.3. Preliminaries

2.3.1. Task Formulation

①Discriminative VQA: for dataset $\mathcal{D}$ with $n$ triplets $\{(v_i,q_i,a_i)\}_{i=1}^n$ , where $v_{i}\in V$ denotes image, $q_{i}\in\mathcal{Q}$ denotes question, $a_{i}\in\mathcal{A}$ denotes answer. By optimizing parameters $\theta^{(\mathrm{d})}$ , models predict the answer:

$\hat{a}_i^{(\mathrm{d})}=\arg\max_{a_i\in\mathcal{A}}p(a_i|v_i,q_i;\theta^{(\mathrm{d})})$

②Generative VQA: for dataset $\mathcal{D}$ , it predicts answers token by token. Thus the optimization goal is maximize the conditional probability $p(y_j|(\hat{y}_1,\ldots,\hat{y}_{j-1}),v_i,q_i;\theta^{(\mathrm{g})})$ :

where $\mathcal{Y}$ is the set of all tokens in the corpus, $k$ denotes the number of tokens in $\hat{a}_i$

2.3.2. VQA Paradigm

（1）Non-Debiasing

①Discriminative VQA: combining patch level image encoder $E_\mathrm{v}:\mathcal{V}\to\mathbb{R}^{n_\mathrm{v}\times d_\mathrm{v}}$ , word-level question encoder $E_\mathrm{q}:\mathcal{Q}\to\mathbb{R}^{n_\mathrm{q}\times d_\mathrm{q}}$ , multi-modality encoder $E_\mathrm{m}:\mathbb{R}^{n_\mathrm{q}\times d_\mathrm{q}}\times\mathbb{R}^{n_\mathrm{v}\times d_\mathrm{v}}\to\mathbb{R}^{d_\mathrm{m}}$ and predictor $E_\mathrm{c}:\mathbb{R}^{d_\mathrm{m}}\to\mathbb{R}^{|\mathcal{A}|}$ . Just like:

$\hat{a}_i^{(\mathrm{d})}=f^{(\mathrm{d})}(v_i,q_i;\theta^{(\mathrm{d})})=E_\mathrm{c}(E_\mathrm{m}(E_\mathrm{v}(v_i),E_\mathrm{q}(q_i)))$

使用不同的/相同的Transformer来替换编码器被作者称为双流/单流方法：

$\hat{a}_i^{(\mathrm{d})}=f^{(\mathrm{d})}(v_i,q_i;\theta^{(\mathrm{d})})=E_\mathrm{c}(E_\mathrm{t}(\boldsymbol{v}_i||\boldsymbol{q}_i))$

②Generative VQA: with patch level image encoder $E_\mathrm{v}:\mathcal{V}\to\mathbb{R}^{n_\mathrm{v}\times d_\mathrm{v}}$ and word-level question encoder $E_\mathrm{q}:\mathcal{Q}\to\mathbb{R}^{n_\mathrm{q}\times d_\mathrm{q}}$ , the decoder directly be $\mathbb{R}^{d_{\mathbf{q}}}\times\mathbb{R}^{d_{\mathbf{v}}}\to\mathbb{R}^{|\mathcal{Y}|}$ . The paradigm is:

$\hat{a}_i^{(\mathrm{g})}=f^{(\mathrm{g})}(q_i,v_i;\theta^{(\mathrm{g})})=\mathrm{Decoder}(E_\mathrm{q}(q_i),E_\mathrm{v}(v_i))$

（2）Debiasing

①Fake connections: Q & key words

②The non-debiasing methods predict answers by:

$\begin{gathered} \hat{a}_{i}^{(\mathrm{l})}=f^{(\mathrm{l})}(v_i,q_i;\theta_\mathrm{l})=E_\mathrm{c}(E_\mathrm{q}(q_i)), \\ \hat{a}_{i}^{(\mathrm{v})}=f^{(\mathrm{v})}(v_i,q_i;\theta_\mathrm{v})=E_\mathrm{c}(E_\mathrm{v}(v_i)), \end{gathered}$

⭐language bias learning is more prevalent than vision bias learning

③Multimodal bias learning:

$\hat{a}_i^{(\mathrm{m})}=f^{(\mathrm{m})}(v_i,q_i;\theta^{(\mathrm{m})})$

2.4. Datasets

2.4.1. In-Distribution Setting

①VQA v1: Q&A with 10 subjects:

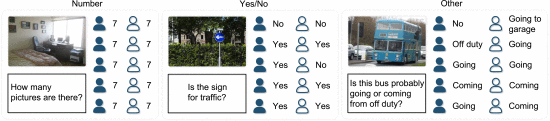
type of answers: "(number)", "Yes/No", "Other" (might be multi true answer in other option)

②VQA v2 (to solve the bias problem in v1): designed similar stimuli with different answer:

but distribution still affects

③TDIUC: COCO based, add 12 types of questions such as positional reasoning and activity recognition

④GQA: more complex question

⑤COVR: only one true answer, and add logical operators such as quantifiers and aggregations

⑥CRIC: contains annotations triples such as the commonsense knowledge “(subject: fork, relation: is used for, object: moving food)”

2.4.2. Out-of-Distribution Setting

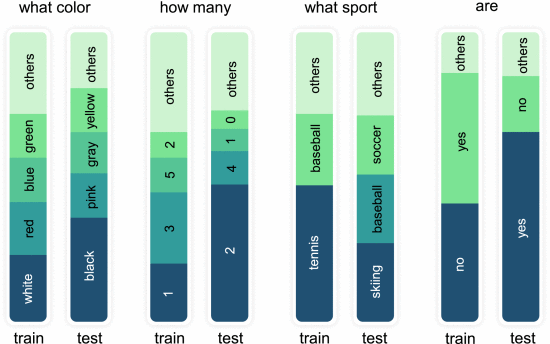
①VQA-CP v1 & VQA-CP v2: 370 K questions with 205 K images are in VQA-CP v1 and 658 K questions with 219 K images are in VQA-CP v2. ⭐There are significant distribution difference between train set and test set:

②GQA-OOD: evaluate ID and OOD performance by answer groups:

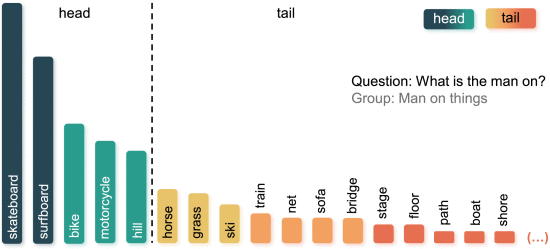
which contains 53 K questions with 9.7 K images

③VQA-Rephrasings: 162.0 K questions with 40.5 K images are used to measure answer changes when question change (just words, which causes fault prediction)

④VQACE: short-cut example:

⑤VQA-VS: provide more specific shortcut

⑥AVQA: 243.0 K questions accompanied by 37.9 K images, collects fail-predicted Q&A

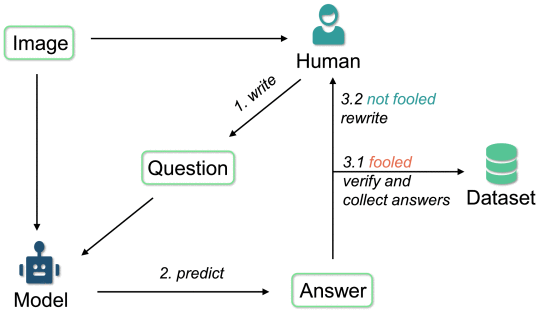
⑦AdVQA: adversarial also, contains 46.8 K questions accompanied by 41.8 K images

⑧Overview of VQA datasets:

2.5. Evaluations

①Open-Ended Accuracy:

$\text{open-endded\,\,accuracy}=\text{min}\left \{ \frac{n_a}{3},1 \right \}$

where $n_a$ denotes the number of predicted answers that are identical to human-provided answers for questions and 3 is the minimum number of consensuses

②Composite Metrics: Consistency, Validity/Plausibility, Distribution, Grounding

③Arithmetic MPT: by TDIUC

④Consensus Score: proposed by VQA-Rephrasings:

$cs(k)=\sum_{\mathcal{Q}^{\prime}\subset\mathcal{Q},|\mathcal{Q}^{\prime}|=k}\frac{s(\mathcal{Q}^{\prime})}{^nC_k}$

$\left.\mathrm{with}s(\mathcal{Q}^{\prime})=\left\{ \begin{array} {ll}1 & \mathrm{if}\quad\forall q\in\mathcal{Q}^{\prime}\quad\phi(q)>0, \\ 0 & \text{otherwise.} \end{array}\right.\right.$

where ${}^nC_k$ is the number of subsets with size $k$ sampled from a set with size $n$ , $\mathcal{Q}^{\prime}$ is a group of questions contained in $\mathcal{Q}$ that consists of $n$ rephrasings, and $\phi(q)$ is the open-ended accuracy.

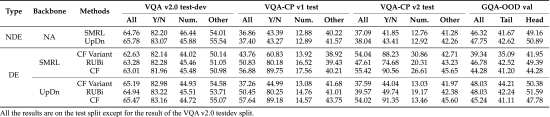
2.6. Debiasing Methods

①Categories: ensemble learning, data augmentation, self-supervised contrastive learning, and answer re-ranking

②Summarizing of existing methods:

③Methods in other dataset:

2.6.1. Ensemble Learning

①Contains combination $\Phi$ of a bias branch $E_b$ :

$\hat{a}_i=\Phi\left(E_\mathrm{b}\left(E_\mathrm{v}(v_i),E_\mathrm{q}(q_i)\right),f(v_i,q_i)\right)$

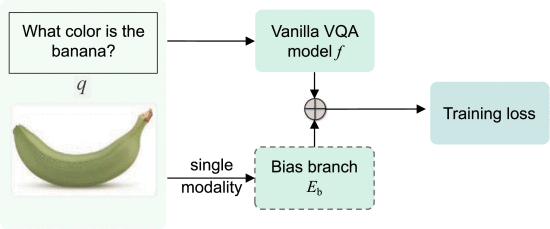
（就是一般测试的时候还是问题和图片都进去学，但这个集成学习是训练的时候用两个模态但测试的时候只用一个模态。看上去有点离谱了，测试为什么只用一个模态？我没理解错吧？↓）

2.6.2. Data Augmentation

①Generate additional ugmented question-answer pairs $\left ( v_i^\prime,q_i^\prime,a_i^\prime \right )$

②Answer prediction:

$\begin{aligned} & \hat{a}_{i}=E_{\mathrm{c}}(E_{\mathrm{m}}(E_{\mathrm{v}}(v_{i}),E_{\mathrm{q}}(q_{i}))), \\ & (v_i,q_i,a_i)\in\mathcal{D}\cup\{(v_i^{\prime},q_i^{\prime},a_i^{\prime})|i\in[1,n]\}. \end{aligned}$

③Main methods: 1) synthetic-based: generate new training samples by modifying regions or words of the original images or questions; 2) pairing-based: generate new samples by re-matching relevant questions for images:

2.6.3. Self-Supervised Contrastive Learning

①Gather similar sample pairs and push dissimilars away

②Loss:

$\mathcal{L}= \lambda_\mathrm{C}\mathcal{L}_\mathrm{C}+\lambda_\mathrm{V}\mathcal{L}_\mathrm{V}, \\ \mathcal{L}_{\mathrm{C}}= \mathbb{E}_{o,p,n\in\mathcal{D}^*}\left[-\log\left(\frac{e^{s(o,p)}}{e^{s(o,p)}+e^{s(o,n)}}\right)\right], \\ \mathcal{L}_{\mathrm{V}} =-\frac{1}{|\mathcal{D}^*|}\sum_{i=1}^{|\mathcal{D}^*|}[a_i]\log\hat{a}_i,$

where $\lambda$ 's are weights, $s(o,p),s(o,n)$ is the scoring function between the anchor $o$ and the positive sample $p$ / negative sample $n$ , $\left|\mathcal{D}^*\right|$ is augmented data, $[a_i]$ is the index of the answer $a_i$

③Schematic of this method:

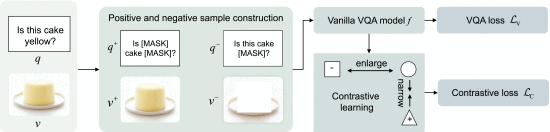
2.6.4. Answer Re-Ranking

①Process:

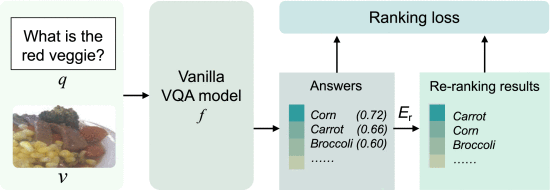
$\hat{a}_i=E_\mathrm{r}(E_\mathrm{c}(E_\mathrm{m}(E_\mathrm{v}(v_i),E_\mathrm{q}(q_i))))$

2.7. Exploring the Robustness of Vision-Language Models for VQA

①Single-stream and dual-stream VLM:

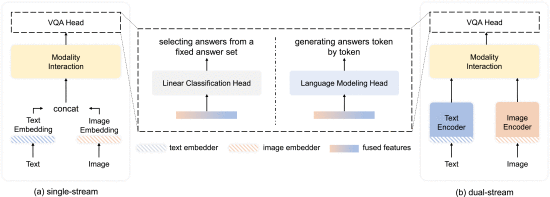
②VQA Results of VLMs in ID and OOD Situations:

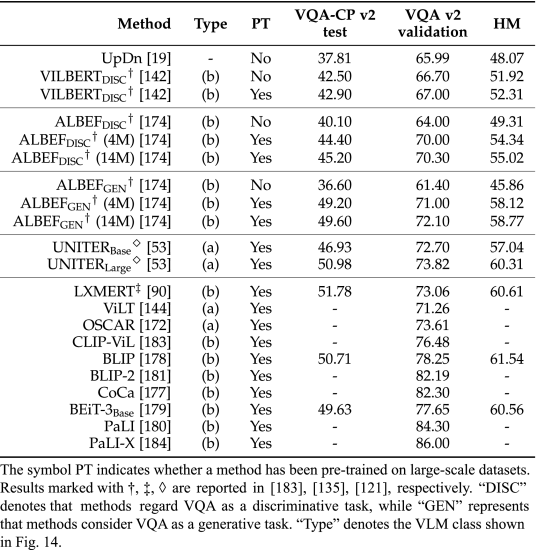
2.8. Discussions and Future Directions

①Limitations: more accurate annotations, ID/OOD tasks contained, metrics of multi-hop inference, accurate evaluation, robust debiasing methods

②Robust evaluation:

2.9. Conclusion

3. Reference

@ARTICLE{10438044,
author={Ma, Jie and Wang, Pinghui and Kong, Dechen and Wang, Zewei and Liu, Jun and Pei, Hongbin and Zhao, Junzhou},
journal={IEEE Transactions on Pattern Analysis and Machine Intelligence},
title={Robust Visual Question Answering: Datasets, Methods, and Future Challenges},
year={2024},
volume={46},
number={8},
pages={5575-5594},
keywords={Sports;Task analysis;Robustness;Transformers;Training;Question answering (information retrieval);Knowledge engineering;Vision-and-language pre-training;bias learning;debiasing;multi-modality learning;visual question answering},
doi={10.1109/TPAMI.2024.3366154}}