最大似然估计，最大后验估计以及贝叶斯估计

1.前言

最大似然估计（Maximum likelihood estimation, 简称MLE）和最大后验概率估计（Maximum a posteriori estimation, 简称MAP）是很常用的两种参数估计方法，如果不理解这两种方法的思路，很容易弄混它们。下文将详细说明MLE和MAP的思路与区别。

1.1什么是参数

在机器学习中，我们经常使用一个模型来描述生成观察数据的过程。例如，我们可以使用一个随机森林模型来分类客户是否会取消订阅服务（称为流失建模），或者我们可以用线性模型根据公司的广告支出来预测公司的收入（这是一个线性回归的例子）。每个模型都包含自己的一组参数，这些参数最终定义了模型本身。

我们可以把线性模型写成 y = mx + c 的形式。在广告预测收入的例子中，x 可以表示广告支出，y 是产生的收入。m 和 c 则是这个模型的参数。这些参数的不同值将在坐标平面上给出不同的直线（见下图）。

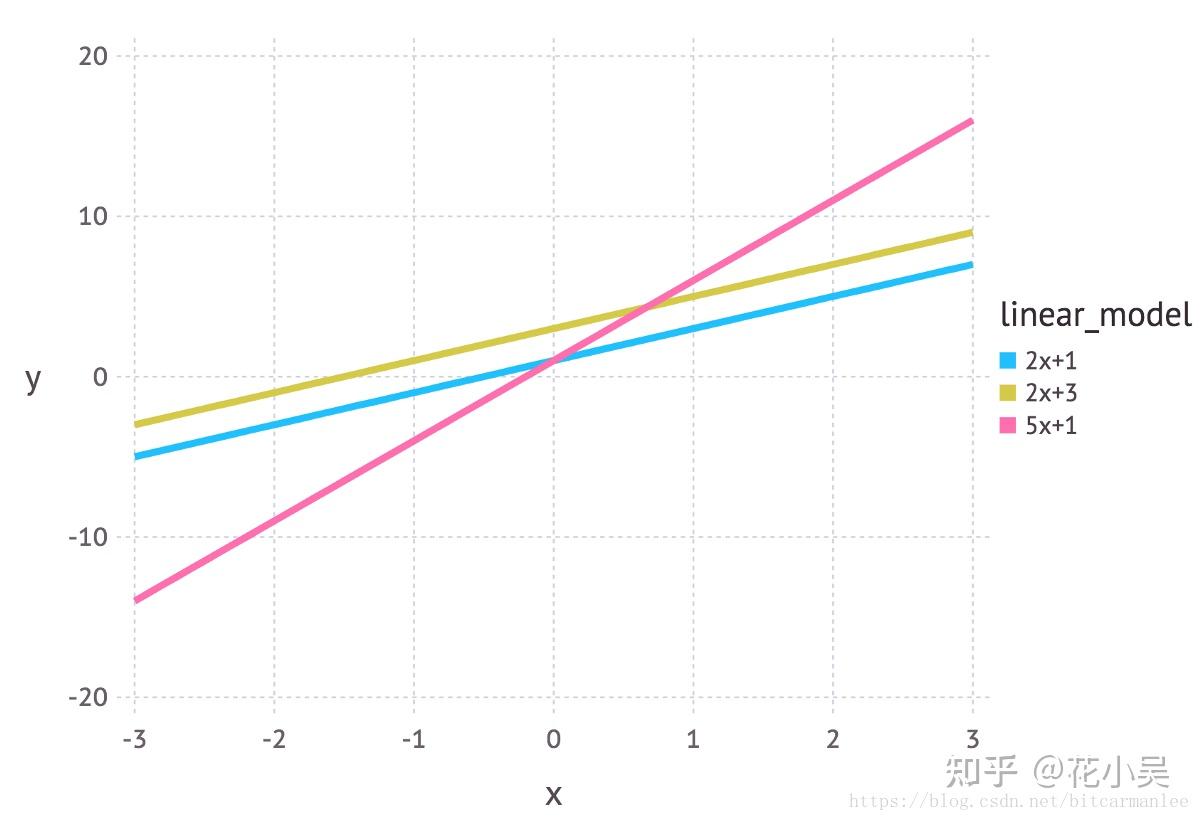
1.2 参数估计的方法

参数估计：根据样本统计量的数值对总体参数进行估计的过程。根据参数估计的性质不同，可以分成两种类型：点估计和区间估计。

点估计：点估计就是用样本统计量的某一具体数值直接推断未知的总体参数。

对总体参数进行点估计常用的方法有两种：矩估计与最大似然估计，其中最大似然估计就是我们实际中使用非常广泛的一种方法。

举例：在进行有关小学生身高的研究中，随机抽取1000名小学生并计算出他们的平均身高为1.45米。如果直接用这个1.45米代表所有小学生的平均身高，那么这种估计方法就是点估计。

优点：按这两种方法对总体参数进行点估计，能够得到相对准确的结果。如用样本均值X估计总体均值，或者用样本标准差S估计总体标准差σ。

缺点：点估计有一个不足之处，即这种估计方法不能提供估计参数的估计误差大小。对于一个总体来说，它的总体参数是一个常数值，而它的样本统计量却是随机变量。当用随机变量去估计常数值时，误差是不可避免的，只用一个样本数值去估计总体参数是要冒很大风险的。因为这种误差风险的存在，并且风险的大小还未知，所以，点估计主要为许多定性研究提供一定的参考数据，或在对总体参数要求不精确时使用，而在需要用精确总体参数的数据进行决策时则很少使用。

区间估计：在推断总体参数时，还要根据统计量的抽样分布特征，估计出总体参数的一个区间，而不是一个数值，并同时给出总体参数落在这一区间的可能性大小，概率的保证。还是举小学生身高的例子，如果用区间估计的方法推断小学生身高，则会给出以下的表达：根据样本数据，估计小学生的平均身高在1.4~1.5米之间，置信程度为95%，这种估计就属于区间估计。

1.3概率与统计的区别

概率（probabilty）和统计（statistics）看似两个相近的概念，其实研究的问题刚好相反。

概率：概率研究的问题是，已知一个模型和参数，怎么去预测这个模型产生的结果的特性（例如均值，方差，协方差等等）。

举例：我想研究怎么养猪（模型是猪），我选好了想养的品种、喂养方式、猪棚的设计等等（选择参数），我想知道我养出来的猪大概能有多肥，肉质怎么样（预测结果）。

统计：统计研究的问题则相反。统计是，有一堆数据，要利用这堆数据去预测模型和参数。

举例：仍以猪为例。现在我买到了一堆肉，通过观察和判断，我确定这是猪肉（这就确定了模型。在实际研究中，也是通过观察数据推测模型是／像高斯分布的、指数分布的、拉普拉斯分布的等等），然后，可以进一步研究，判定这猪的品种、这是圈养猪还是跑山猪还是网易猪，等等（推测模型参数）。

总结：概率是已知模型和参数，推数据。统计是已知数据，推模型和参数。

显然，对于最大似然估计，最大后验估计，贝叶斯估计来说，它们都是用来推测参数的方法，都属于统计的范畴。

而最大最大似然估计（MLP）与最大后验估计（MAP）是两种不同的方法，可通过贝叶斯思想进行解释。

2.贝叶斯公式含义

贝叶斯公式就是在描述，你有多大把握能相信一件证据？（how much you can trust the evidence）

学习机器学习和模式识别的人一定都听过贝叶斯公式(Bayes’ Theorem)：

将分母展开可得:

举例：一辆汽车（或者电瓶车）的警报响了，你通常是什么反应？有小偷？撞车了？ 不。。 你通常什么反应都没有。因为汽车警报响一响实在是太正常了！每天都要发生好多次。本来，汽车警报设置的功能是，出现了异常情况，需要人关注。然而，由于虚警实在是太多，人们渐渐不相信警报的功能了。

贝叶斯公式就是在描述，你有多大把握能相信一件证据？（how much you can trust the evidence）

我们假设响警报的目的就是想说汽车被砸了。把A计作“汽车被砸了”，B计作“警报响了”，带进贝叶斯公式里看。我们想求等式左边发生 P(A∣B) 的概率，这是在说警报响了，汽车也确实被砸了。汽车被砸从而引起警报响，即 P(B∣A) 。但是，也有可能是汽车被小孩子皮球踢了一下、被行人碰了一下等其他原因（其他原因全部计作 A¯ ），其他原因引起汽车警报响了，即 P(B∣A¯) 。那么，现在突然听见警报响了，这时汽车已经被砸了的概率是多少呢（这即是说，警报响这个证据有了，多大把握能相信它确实是在报警说汽车被砸了）？想一想，应当这样来计算。用警报响起、汽车也被砸了这事件的数量，除以响警报事件的数量（这即【式1】）。进一步展开，即警报响起、汽车也被砸了的事件的数量，除以警报响起、汽车被砸了的事件数量加上警报响起、汽车没被砸的事件数量（这即【式2】）。

再思考【式2】。想让 P(A∣B)=1 ，即警报响了，汽车一定被砸了，该怎么做呢？让 P(B∣A¯)P(A¯)=0 即 可 。 很 容 易 想 清 楚 ， 假 若 让 P(A¯)=0 即可，即杜绝了汽车被球踢、被行人碰到等等其他所有情况，那自然，警报响了，只剩下一种可能——汽车被砸了。这即是提高了响警报这个证据的说服力。

从这个角度总结贝叶斯公式：做判断的时候，要考虑所有的因素。 老板骂你，不一定是你把什么工作搞砸了，可能只是他今天出门前和太太吵了一架。

再思考【式2】。观察【式2】右边的分子， P(B∣A) 为汽车被砸后响警报的概率。假设认为这是1吧。但是，若 P(A) 很小，即汽车被砸的概率本身就很小，则 P(B∣A)P(A) 仍然很小，即【式2】右边分子仍然很小， P(A∣B) 还是大不起来。 这里， P(A) 即是常说的先验概率，如果A的先验概率很小，就算 P(B∣A) 较大，可能A的后验概率 P(A∣B) 还是不会大（假设 P(B∣A¯)P(A¯) 不变的情况下）。

从这个角度思考贝叶斯公式：一个本来就难以发生的事情，就算出现某个证据和他强烈相关，也要谨慎。证据很可能来自别的虽然不是很相关，但发生概率较高的事情。 发现刚才写的代码编译报错，可是我今天状态特别好，这语言我也很熟悉，犯错的概率很低。因此觉得是编译器出错了。 ————别，还是先再检查下自己的代码吧。

3.概率函数和似然函数的区别

似然（likelihood）这个词其实和概率（probability）是差不多的意思，Colins字典这么解释：The likelihood of something happening is how likely it is to happen. 你把likelihood换成probability，这解释也读得通。但是在统计里面，似然函数和概率函数却是两个不同的概念（其实也很相近就是了）。

对于函数P(x∣θ) ，输入又两个：

x表示某一个具体的数据； θ 表示模型的参数。

概率函数：如果 θ 是已知确定的，x是变量，这个函数叫做概率函数(probability function)，它描述对于不同的样本点x，其出现概率是多少。（相当于机器/深度学习模型的测试过程，此时参数已训练好，是确定的）

似然函数：如果x是已知确定的， θ 是变量，这个函数叫做似然函数(likelihood function), 它描述对于不同的模型参数，出现x这个样本点的概率是多少。（相当于机器/深度学习模型的训练过程，此时参数还未确定，x是确定的）

举例：

这有点像“一菜两吃”的意思。其实这样的形式我们以前也不是没遇到过。例如， f(x,y)=xy , 即x的y次 方。如果x是已知确定的(例如x=2，这就是 )，这就是 f(y)=2y , 这是指数函数。如果y是已知确定的(例如y=2)这就是 f(x)=x2 ，这是二次函数。同一个数学形式，从不同的变量角度观察，可以有不同的名字。

4.最大似然估计(maximum likelihood estimates，MLE)

最大似然估计就是给定模型，然后通过收集数据，求该模型的参数

前文提到，最大似然估计(maximum likelihood estimates，MLE)是实际中使用非常广泛的一种方法，用我们老师的一句最简单的话来总结最大似然估计，就是“谁大像谁”。说到最大似然估计与最大后验估计，最好的例子自然就是抛硬币了。本文也不免俗，同样以抛硬币作为例子。

例如，投10次特殊的硬币（给定模型），出现7次正面3次反面（请注意，这里10次结果有顺序，后面所有的投硬币结果，都有顺序）（收集数据），现在要估计投这枚硬币出现正面的概率（求参数）。

举例：

问题：假设有一个造币厂生产某种硬币，现在我们拿到了一枚这种硬币，想试试这硬币是不是均匀的。即想知道抛这枚硬币，正反面出现的概率（记为 θ ）各是多少？

解答：这是一个统计问题，回想一下，解决统计问题需要什么？ 数据！

于是我们拿这枚硬币抛了10次，得到的数据x是：反正正正正反正正正反。我们想求的正面概率 θ 是模型参数，而抛硬币模型我们可以假设是二项分布。（根据补充的二项分布公式进行理解）

即进行多次实验，每次实验只有两种可能。用x0，x1，…，x9表示这10次投硬币的结果，用 θ 表示投该硬币出现正面的概率，那么把我们的直觉写成用数学写出来就是似然函数，出现实验结果 x （即反正正正正反正正正反）的似然函数是可表示成：

(此时x是已知的，参数 θ 是未知的，它描述对于不同的模型参数，出现x这个样本点的概率是多少)

注：这是个只关于 θ 的函数。而最大似然估计，顾名思义，就是要最大化这个函数，说得更简单点，就是给你一个函数，求它的极大值点。

我们可以画出 f(θ) 的图像：

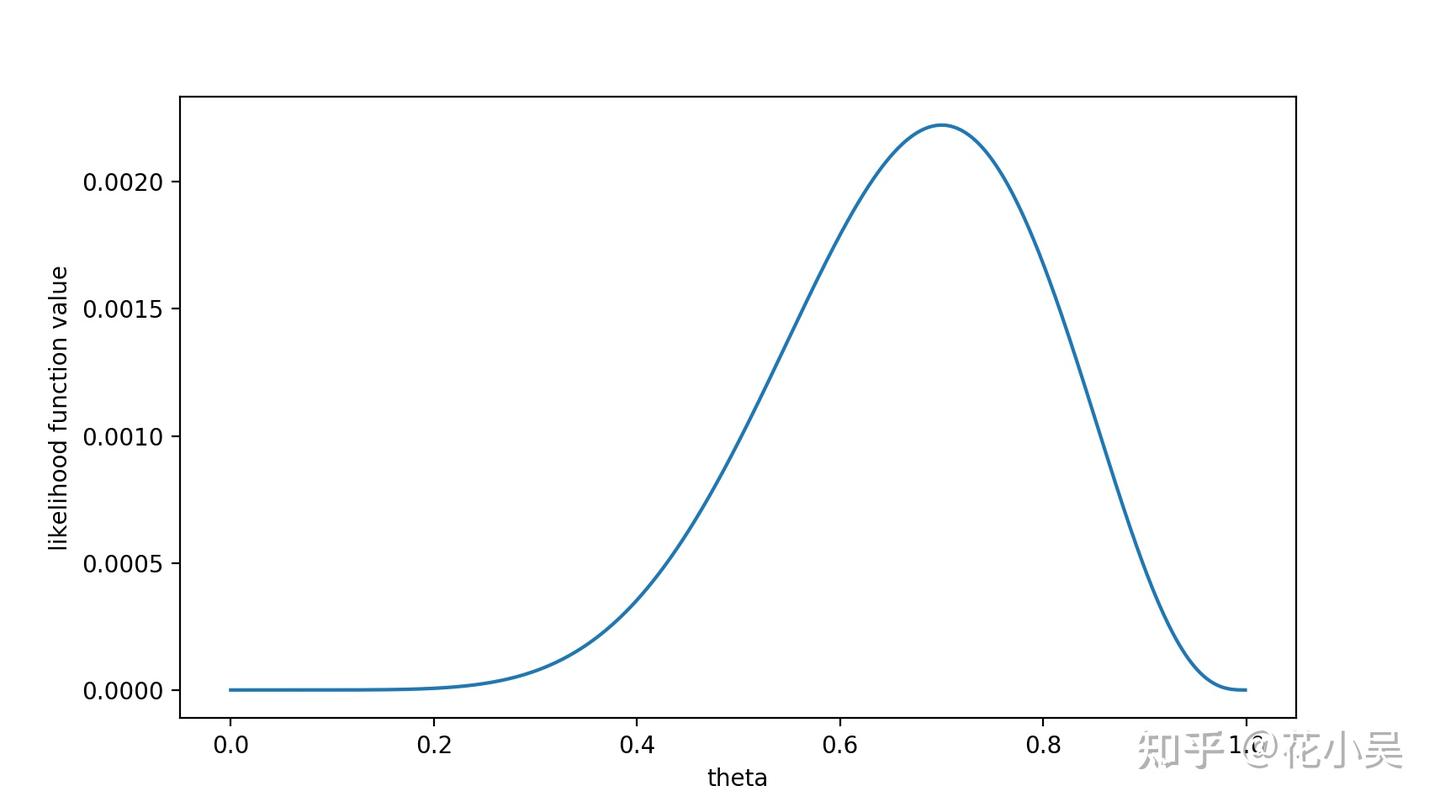
从图中我们可以看出，在 θ=0.7 时，似然函数能取到最大值，（也就是说，在模型参数θ = 0.7时，出现x这个样本点的概率最大。）当然实际中我们一般不会画图，而是通过更为简洁的数学手段来处理。首先我们取对数似然函数，这样更方便后续的数学运算：

注：在模型参数（正面向上概率）θ = 0.7时，出现x这个样本点的概率最大，就是在θ = 0.7时，抛掷硬币最有可能出现x这个样本点这种情况。所以最大似然函数的结果就表示为在似然函数取得最大值时（最有可能的概率），此时的模型参数是多少。

（1）取对数：

对似然函数取对数，不会影响该函数的单调性，从而不会影响最后的计算的极值，也可以在一定程度上减少因计算而带来的误差，还可以极大的简化计算。 此时求解取对数的似然函数的极大值点，就是似然函数的极大值点。由于似然函数是先单调递增，然后再单调递减的，因此，取对数的似然函数导数为0的点，即是似然函数或取对数的似然函数的极大值点（在这里也是最大值点）

最大似然估计可以转化为求下面式子的解：

（2）求导：

（3）令导数为0：

（4）求解

这样，我们已经完成了对 θ 的最大似然估计。即抛10次硬币，发现7次硬币正面向上，最大似然估计认为正面向上的概率是0.7。是不是非常直接，非常简单粗暴？没错，就是这样，谁大像谁！

如果未知参数有多个，则需要用取对数的似然函数对每个参数进行求偏导，使得所有偏导均为0的值，即为该函数的极值点，一般也是其最大似然估计值。

（最大似然估计就是根据样本的正反面情况，推导出正面向上的概率）

说到这里为止，可能很多同学不以为然：你这不坑爹嘛？只要硬币一枚正常硬币，不存在作弊情况，正面朝上的概率必然为0.5么，你这怎么就忽悠我们是0.7呢。OK，如果你这么想，恭喜你，那你就天然包含了贝叶斯学派的思想！我们所谓的正常硬币向上的概率为0.5，就是贝叶斯里的先验概率。

注：这里就包含了贝叶斯学派的思想了——要考虑先验概率。 为此，引入了最大后验概率估计。

补充：二项分布，伯努利分布

二项分布：在概率论和统计学中，二项分布（Binomial distribution）是n个独立的是/非试验中成功的次数的离散概率分布，其中每次试验的成功概率为p。这样的单次成功/失败试验又称为伯努利试验。实际上，当n=1时，二项分布就是伯努利分布。

二项分布的概率质量函数可以简写为X~B(n,p)。

伯努利分布：（Bernoulli distribution，又名两点分布或者0-1分布，是一个离散型概率分布，为纪念瑞士科学家雅各布·伯努利而命名。)若伯努利试验成功，则伯努利随机变量取值为0。记其成功概率为 p(0≤p≤1) ，失败概率为 q=1−p。

对于伯努利分布来说，其概率质量函数为：

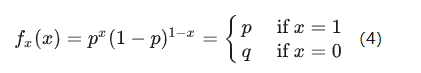
期望为： 

方差为： 

而如果X ~ B(n, p)（也就是说，X是服从二项分布的随机变量），一般的二项分布是n次独立的伯努利试验的和。它的期望值和方差分别等于每次单独试验的期望值和方差的和：

5.最大后验概率估计(maximum a posteriori estimation，MAP)

最大后验（Maximum A Posteriori，MAP）估计可以利用经验数据获得对未观测量的点态估计。它与Fisher的最（极）大似然估计（Maximum Likelihood，ML）方法相近，不同的是它扩充了优化的目标函数，其中融合了预估计量的先验分布信息，所以最大后验估计可以看作是正则化（regularized）的最大似然估计。

对于最大后验概率估计，我们先进行通俗简单的理解，还是以刚才的那个问题为例，投10次硬币，结果分别是x0,x1,…,x9，出现了7次正面，3次反面。

现在，有两个人A和B，其中A觉得那枚硬币，它就是一个一般的硬币，出现正面的概率θ = 0.5。而B觉得，它是一个特殊的硬币，出现正面的概率θ = 0.7。

最大后验概率就是把他们的假设都进行计算（验算），然后选择其中假设最好的一个，当作最大后验概率。

然后再来计算一下B的假设，假设出现正面的概率θ = 0.7，那么此时，投10次该硬币，出现7次正面的概率则是：

通过计算，我们可以很直观的发现，相比于A的假设，B的假设准确的概率更大一下，当然，这里也不能说B绝对是正确的，只是B是对的可能性更大。我们一般也更相信B的猜测。

5.1定义理解：

最大似然估计：求参数 θ , 使似然函数 P(x|θ) 最大。

最大后验概率估计：求参数 θ ,使 P(x|θ)P(θ) 最大. 求得的 θ 不单单让似然函数大， θ 自己出现的先验概率 P(θ) 也得大。 （这有点像正则化里加惩罚项的思想，不过正则化里是利用加法，而MAP里是利用乘法）

（个人认为这里对我理解很重要，与最大似然估计比，多乘了一个先验概率）

MAP其实是在最大化 P(θ∣x)=P(x∣θ)P(θ)P(x) ，不过因为 x 是确定的（即投出的“反正正正正反正正正反”）， P(x) 是一个已知值，所以去掉了分母 P(x) （假设“投10次硬币”是一次实验，实验做了1000次，“反正正正正反正正正反”出现了n次，则 P(x)=n/1000 。总之，这是一个可以由数据集得到的值）。最大化 P(θ∣x) 的意义也很明确， x 已经出现了，要求 θ 取什么值使 P(θ∣x) 最大。顺带一提， P(θ∣x) 即后验概率，这就是“最大后验概率估计”名字的由来。

结合公式理解:

最大似然估计MLE其实就是求一组能够使似然函数最大的参数，即:

如果我们把问题稍微弄复杂一点，如果这个参数 θ 有一个先验概率呢？比如上面的例子中，实际生活经验告诉我们，硬币一般都是均匀的，也就是 θ=0.5 的概率最大，那么这个参数该怎么估计？这个时候就用到了我们的最大后验概率MAP。MAP的基础是贝叶斯公式：

其中， p(x∣θ) 就是之前讲的似然函数， p(θ) 是先验概率，是指在没有任何实验数据的时候对参数 θ 的经验判断，对于一个硬币，大概率认为他是正常的，正面的概率为0.5的可能性最大。

MAP优化的就是一个后验概率，即给定了观测值以后使后验概率最大：

最大后验概率估计就是在已知一系列结果的情况下，求参数可能的最大的那一个，也就是求解下面式子：

就是在序列x0 , x1 , … , xn已知的情况下，θ等于某个值的概率，然后求出θ一个个的取完所有的值的所有概率，选择其中使概率最大的那一个的θ，即为最大后验概率。

从上面公式可以看出， p(x|θ) 是似然函数，而 p(θ) 就是先验概率。对其取对数：

5.2情况1：假设 p(θ) 是 β 分布

通过MAP最终的式子不难看出，MAP就是多个作为因子的先验概率 p(θ) 。这个 p(θ) 可以是任何的概率分布，比如高斯分布，比如也可以是 β 分布。比如 β(5,2) 的概率分布图如下：

因子：8的因子有1，2，4，8

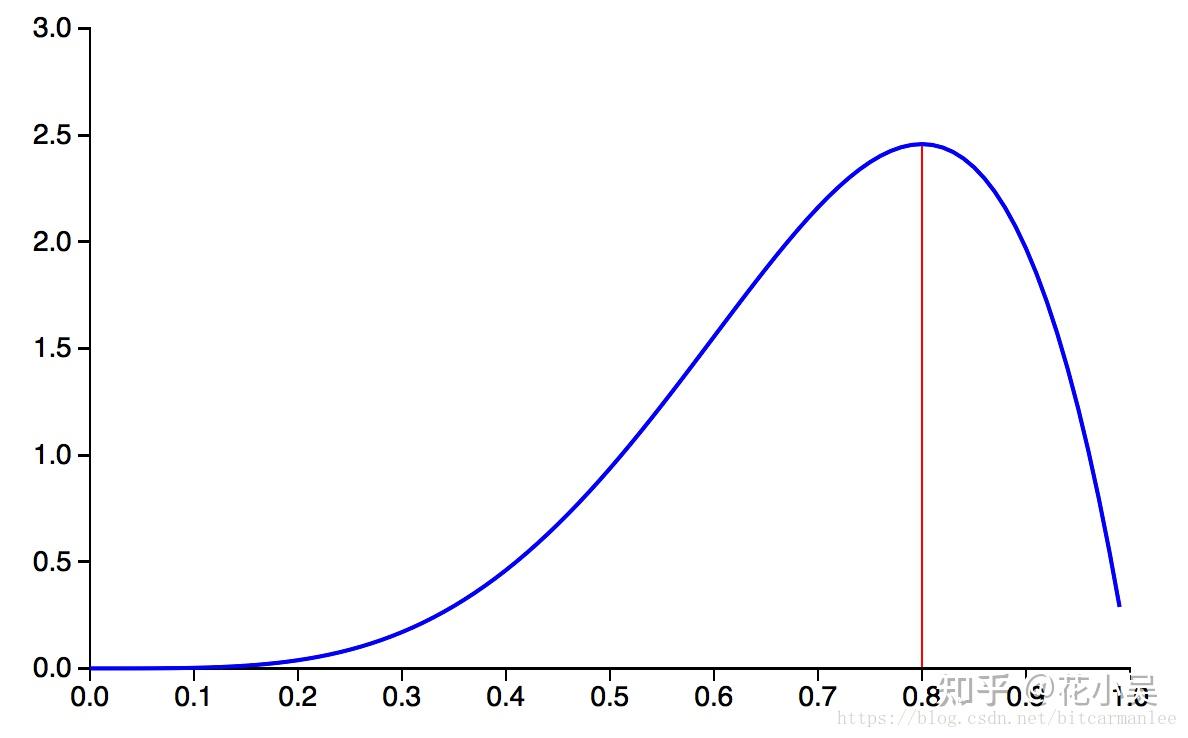
如果将这个概率分布作为 p(θ) ，那么我们在还未抛硬币前，便认为 θ 很可能接近于0.8，而不大可能是个很小的值或是一个很大的值。换言之，我们在抛硬币前，便估计这枚硬币更可能有0.8的概率抛出正面。

那么问题就来了，为什么我们要用 β 分布来描述先验概率呢？

首先一点，通过调节 β 分布中的a和b,你可以让这个概率分布变成各种你想要的形状！β 分布已经很足够表达我们事先对 θ 的估计了。更重要的一点是，如果使用 β 分布，会让之后的计算更加方便。因为有如下结论：

p(θ) 是个 β 分布，那么在观测到"X = 抛10次硬币出现7次正面"的事件后， p(θ|X) 仍然是个 β 分布，只不过此时概率分布的形状因为有了观测事件而发生了变化！此时有:

换句话说，数据观测前后，对 θ 的估计的概率分布均为 β 分布，这就是为什么使用 β 分布方便我们计算的原因。当我们得知 p(θ∣X)=β⁡(θ∣a+3,b+2) 后，只要根据 β 分布的特性，得出 θ 最有可能等于多少了。即 θ 等于多少时，观测后得到的 β 分布有最大的概率密度。

共轭性 共轭先验

到此为止，我们可以得到“共轭性”的真正含义了！后验概率分布（正⽐于先验和似然函数的乘积）拥有与先验分布相同的函数形式。这个性质被叫做共轭性（Conjugacy）。共轭先验（conjugate prior）有着很重要的作⽤。它使得后验概率分布的函数形式与先验概率相同，因此使得贝叶斯分析得到了极⼤的简化。例如，二项分布的参数之共轭先验就是我们前面介绍的 β 分布。多项式分布的参数之共轭先验则是 Dirichlet 分布，⽽⾼斯分布的均值之共轭先验是另⼀个⾼斯分布。

总的来说，对于给定的概率分布 p(X|θ) ，我们可以寻求一个与该似然函数 p(X|θ) 共轭的先验分布 p(θ) ，如此一来后验分布 p(θ|X) 就会同先验分布具有相同的函数形式。而且对于任何指数族成员来说，都存在有一个共轭先验。

5.3情况2：假设 p(θ) 是均值0.5，方差0.1的高斯函数（注意是一个函数，不是具体的值），如下图：

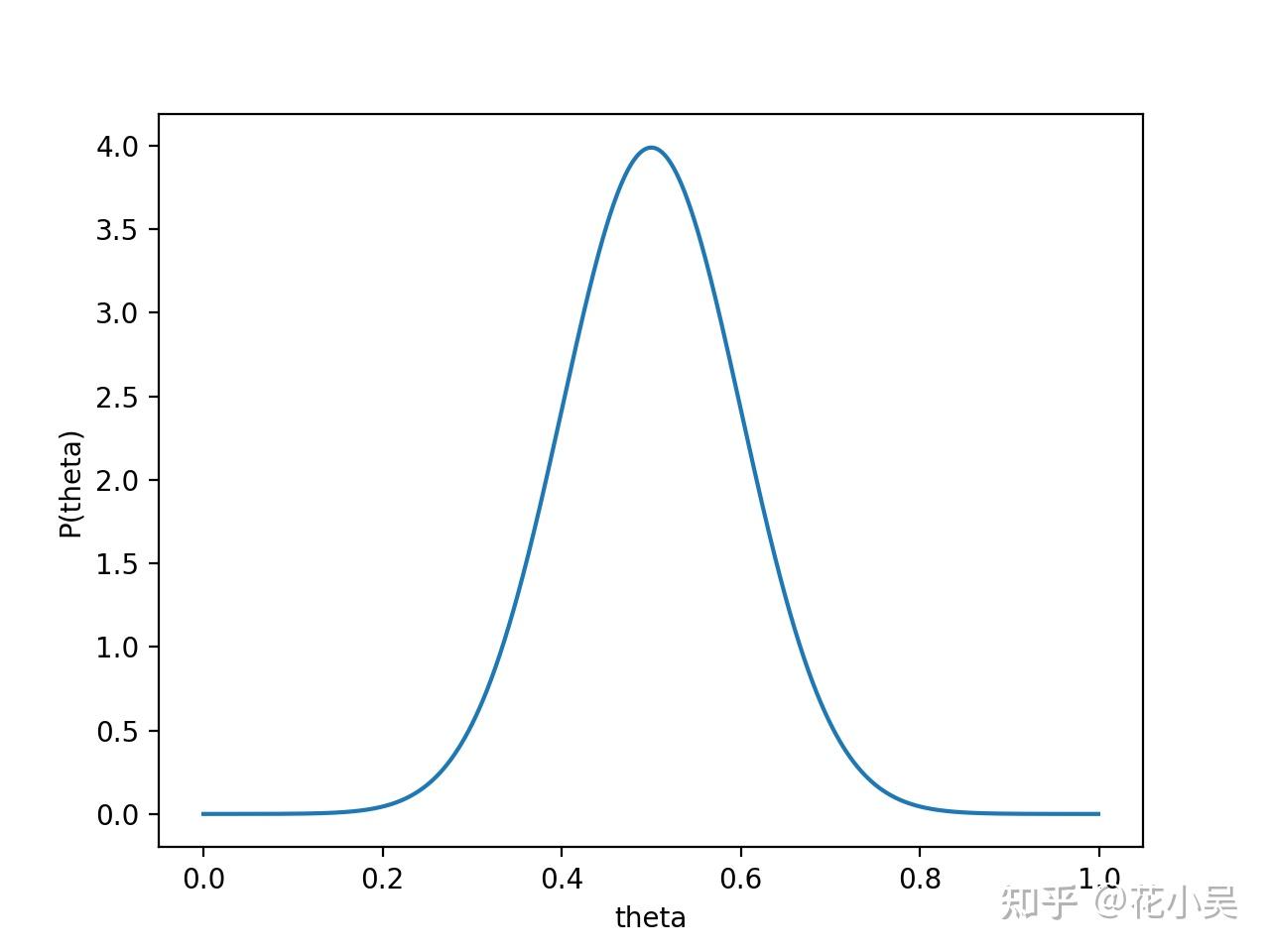
则 P(x∣θ)P(θ) 的函数图像为：

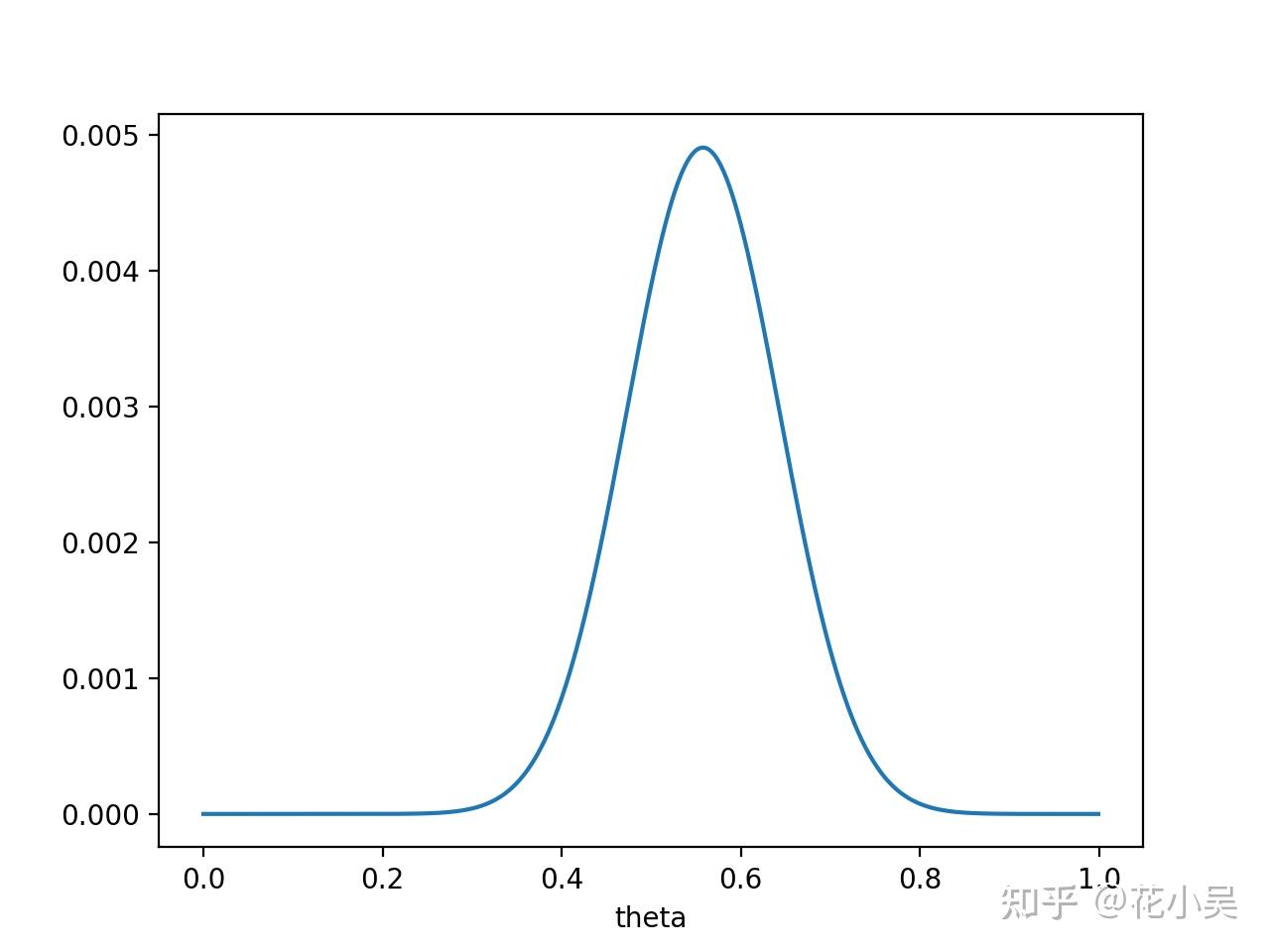
注意，此时函数取最大值时， θ 取值已向左偏移，不再是0.7。实际上，在 θ=0.558 时函数取得了最大值。即，用最大后验概率估计，得到 θ=0.558

最后，那要怎样才能说服一个贝叶斯派相信 θ=0.7 呢？你得多做点实验。。

如果做了1000次实验，其中700次都是正面向上，这时似然函数为:

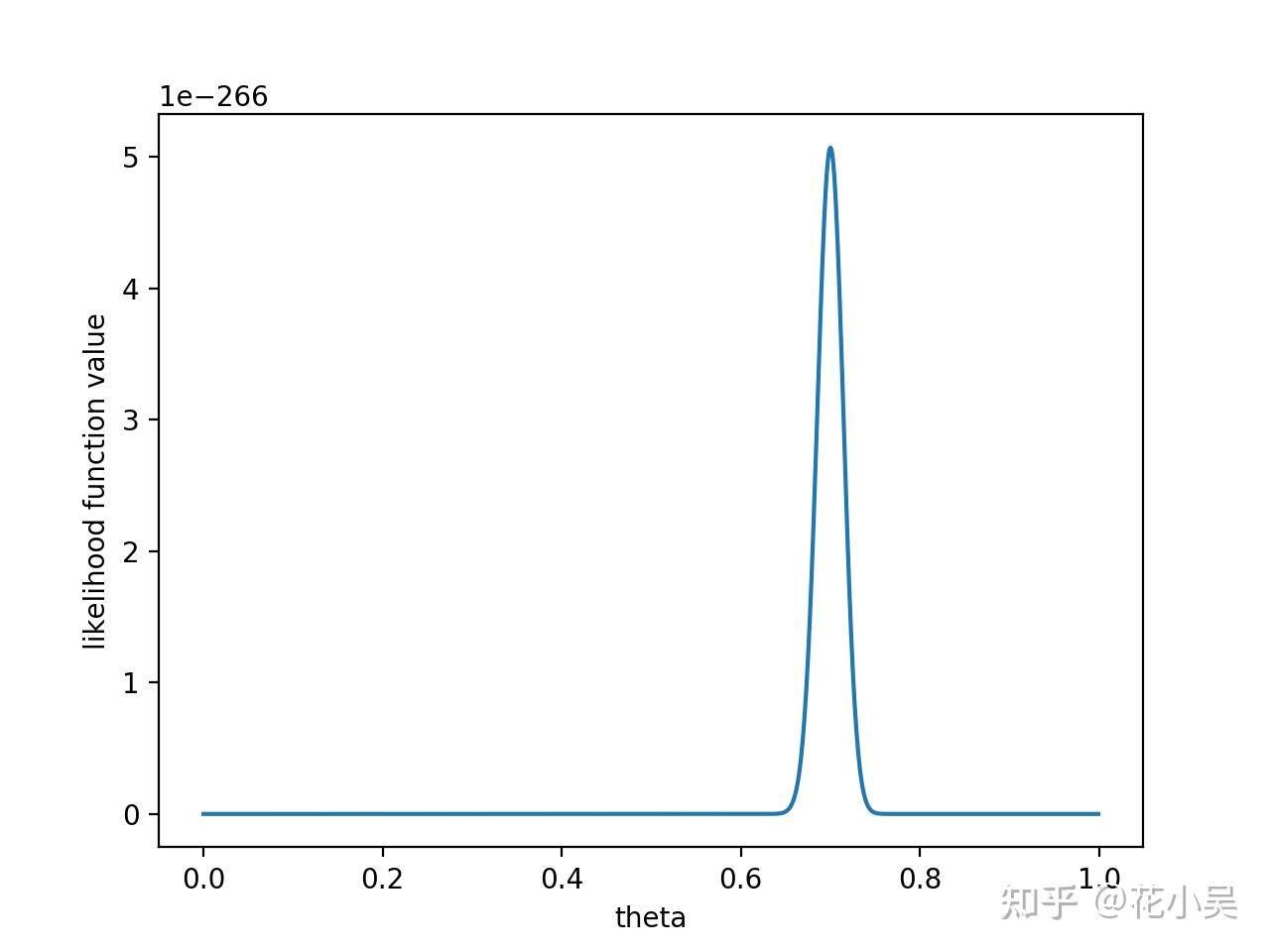
如果仍然假设 P(θ) 为均值0.5，方差0.1的高斯函数， P(x|θ)P(θ) 的函数图像为：

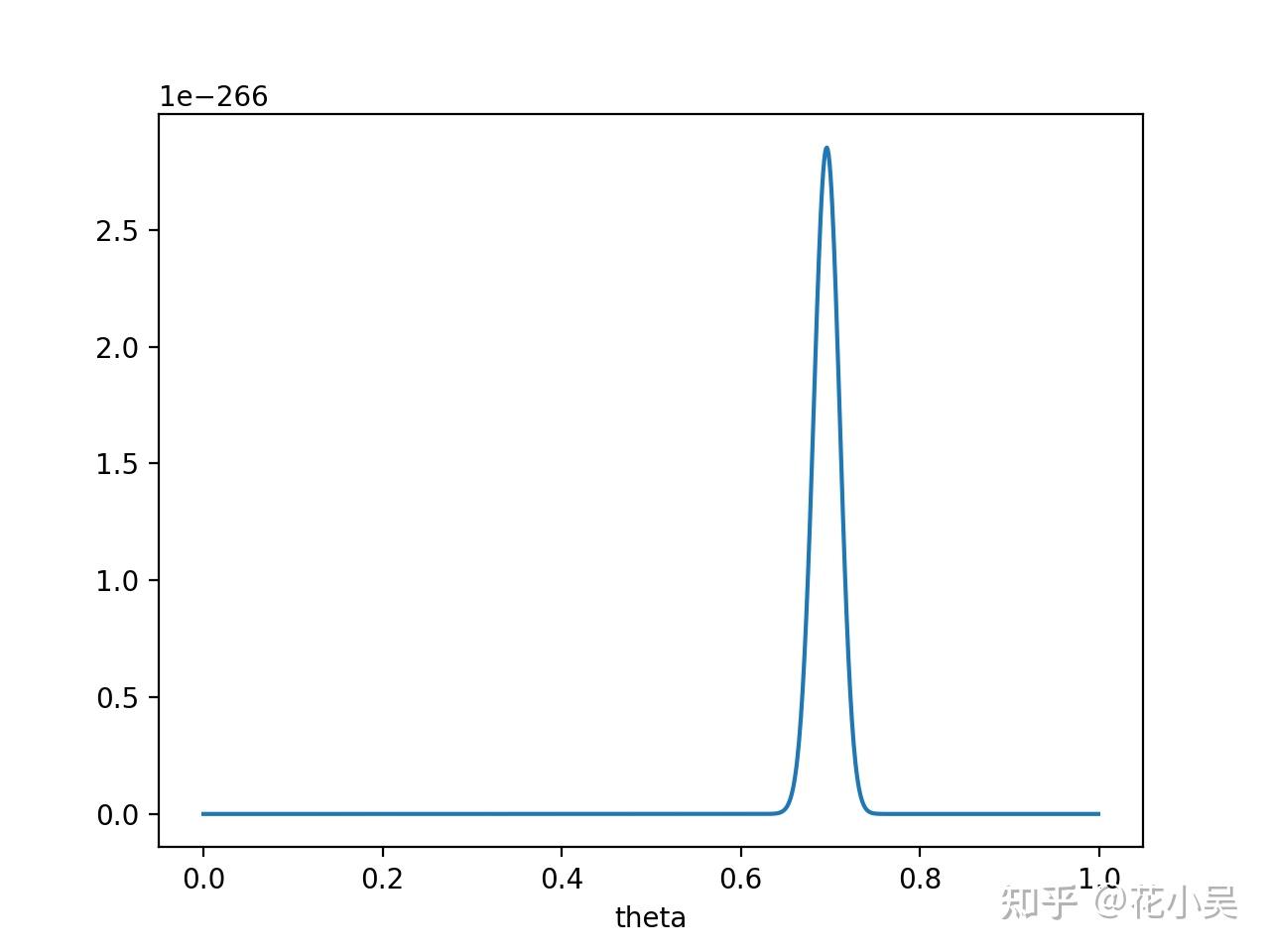
在 θ=0.696 处， P(x∣θ)P(θ) 取得最大值。这样，就算一个考虑了先验概率的贝叶斯派，也不得不承认得把 θ 估计在0.7附近了。

PS. 要是遇上了顽固的贝叶斯派，认为 P(θ=0.5)=1 ，那就没得玩了。。 无论怎么做实验，使用MAP估计出来都是 θ=0.5 。这也说明，一个合理的先验概率假设是很重要的。（通常，先验概率能从数据中直接分析得到）

最大后验的实质就是对参数的每一个可能的取值，都进行极大似然估计，并根据这个取值可能性的大小，设置极大似然估计的权重，然后选择其中最大的一个，作为最大后验估计的结果。

6.最大似然估计和最大后验概率估计的区别

相信读完上文，MLE和MAP的区别应该是很清楚的了。MAP就是多个作为因子的先验概率 P(θ) 。或者，也可以反过来，认为MLE是把先验概率 P(θ) 认为等于1，即认为 θ 是均匀分布。

6.1什么时候最大后验概率估计与最大似然估计相等

当先验分布均匀之时，MAP 估计与 MLE 相等。直观讲，它表征了最有可能值的任何先验知识的匮乏。在这一情况中，所有权重分配到似然函数，因此当我们把先验与似然相乘，由此得到的后验极其类似于似然。因此，最大似然方法可被看作一种特殊的 MAP。

如果先验认为这个硬币是概率是均匀分布的，被称为无信息先验( non-informative prior )，通俗的说就是“让数据自己说话”，此时贝叶斯方法等同于频率方法。随着数据的增加，先验的作用越来越弱，数据的作用越来越强，参数的分布会向着最大似然估计靠拢。而且可以证明，最大后验估计的结果是先验和最大似然估计的凸组合。

7.贝叶斯估计

贝叶斯估计是在MAP上做进一步拓展，此时不直接估计参数的值，而是允许参数服从一定概率分布。回忆下贝叶斯公式：

现在我们不要求后验概率最大，这个时候就需要求 p(X) ，即观察到的X的概率。一般来说，用全概率公式可以求 p(X)

那么如何用贝叶斯估计来预测呢？如果我们想求一个值 x^ 的概率，可以用下面的方法