作者水平有限,欢迎大家提出文中错误
电路理论
图的矩阵表示——邻接矩阵
假设一个图有
m
m
m条边和
n
n
n个节点,那么这个图的邻接矩阵就是
G
m
∗
n
(
G
f
o
r
g
r
a
p
h
)
G_{m*n}(G\ for\ graph)
Gm∗n(G for graph),其中,元素
a
i
j
a_{ij}
aij代表了图的第
i
i
i个边是否与节点
j
j
j相连,如果图是有向图,那么这个元素的正负分别代表了流出和流入。

这个图的邻接矩阵为
G
=
[
1
−
1
0
0
0
1
−
1
0
1
0
−
1
0
1
0
0
−
1
0
0
1
−
1
]
G=\left[ \begin{matrix} 1&-1&0&0\\ 0&1&-1&0\\ 1&0&-1&0\\ 1&0&0&-1\\ 0&0&1&-1\\ \end{matrix} \right]
G=⎣⎢⎢⎢⎢⎡10110−110000−1−101000−1−1⎦⎥⎥⎥⎥⎤
回路
G
=
[
1
−
1
0
0
0
1
−
1
0
1
0
−
1
0
]
G=\left[ \begin{matrix} 1&-1&0&0\\ 0&1&-1&0\\ 1&0&-1&0\\ &&&\\ &&&\\ \end{matrix} \right]
G=⎣⎢⎢⎢⎢⎡101−1100−1−1000⎦⎥⎥⎥⎥⎤
观察边1,2,3,发现他们构成了一个回路
同时这部分矩阵的行不是线性无关的,在邻接矩阵中,线性相关代表着回路,如果一个子图是一个树,那么其对应的子矩阵秩等于边数
零空间
G
ϕ
=
0
G\phi=0
Gϕ=0
ϕ
=
[
ϕ
1
ϕ
2
ϕ
3
ϕ
4
]
T
\phi=[\phi_1\ \phi_2\ \phi_3\ \phi_4]^T
ϕ=[ϕ1 ϕ2 ϕ3 ϕ4]T
G
ϕ
=
[
ϕ
1
−
ϕ
2
ϕ
2
−
ϕ
3
ϕ
1
−
ϕ
3
ϕ
1
−
ϕ
4
ϕ
3
−
ϕ
4
]
=
[
u
1
u
2
u
3
u
4
u
5
]
=
u
G\phi= \left[ \begin{matrix} \phi_1-\phi_2\\ \phi_2-\phi_3\\ \phi_1-\phi_3\\ \phi_1-\phi_4\\ \phi_3-\phi_4\\ \end{matrix} \right]= \left[ \begin{matrix} u_1\\ u_2\\ u_3\\ u_4\\ u_5\\ \end{matrix} \right]=u
Gϕ=⎣⎢⎢⎢⎢⎡ϕ1−ϕ2ϕ2−ϕ3ϕ1−ϕ3ϕ1−ϕ4ϕ3−ϕ4⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡u1u2u3u4u5⎦⎥⎥⎥⎥⎤=u
如果将
ϕ
\phi
ϕ定义为节点的电势
那么
G
ϕ
G\phi
Gϕ就是各边上的电势差,
G
G
G包含的拓扑信息,同时规定了各边的正方向
N
(
G
)
N(G)
N(G)中向量的意义就是电势差为零的节点电势状态
[
1
1
1
1
1
]
[1\ 1\ 1\ 1\ 1]
[1 1 1 1 1]是
N
(
G
)
N(G)
N(G)的一个基,同时通过计算可以知道
r
a
n
k
G
=
1
rank\ G=1
rank G=1所以这个基可以张成整个零空间。
这个解代表了什么,代表了各点电势相等,所以边上没有电势差
如果想确定下来这个电势相等的状态还差什么,在微分方程中,确定解需要一个初始条件,这里也缺的是这样的一个边界条件。比如可以将节点4接地,规定其电势为0(实际上选哪个节点都无所谓,因为任意三列都线性无关)。
由于
ϕ
4
=
0
\phi_4=0
ϕ4=0所以方程化为
G
′
ϕ
=
[
−
1
1
0
0
−
1
1
−
1
0
1
−
1
0
0
0
0
−
1
]
[
ϕ
1
ϕ
2
ϕ
3
]
=
0
G'\phi=\left[ \begin{matrix} -1&1&0\\ 0&-1&1\\ -1&0&1\\ -1&0&0\\ 0&0&-1\\ \end{matrix} \right] \left[ \begin{matrix} \phi_1\\ \phi_2\\ \phi_3\\ \end{matrix} \right]=0
G′ϕ=⎣⎢⎢⎢⎢⎡−10−1−101−10000110−1⎦⎥⎥⎥⎥⎤⎣⎡ϕ1ϕ2ϕ3⎦⎤=0
G
′
G'
G′列满秩,解唯一
左零空间
G
T
i
=
0
G^Ti=0
GTi=0
如果定义
i
i
i为各边的电流强度,就得到了一个代表净流入各节点的电流强度的向量
而
G
T
i
=
0
G^Ti=0
GTi=0,正是基尔霍夫电流定律KCL
O h m ′ s l a w Ohm's\ law Ohm′s law
向量
u
u
u和向量
i
i
i分别代表着各边上的电压值和电流值,如果电路各支路之间无耦合
u
=
[
R
e
d
g
e
1
R
e
d
g
e
2
⋱
R
e
d
g
e
5
]
i
u=\left[ \begin{matrix} R_{edge_1}&&&\\ &R_{edge_2}&&\\ &&\ddots&\\ &&&R_{edge_5}\\ \end{matrix} \right]i
u=⎣⎢⎢⎡Redge1Redge2⋱Redge5⎦⎥⎥⎤i
这个对角矩阵叫做阻抗矩阵
Z
Z
Z,描述了各边上电压值和电流值得关系,注意,阻抗矩阵不一定是对角阵,比如电路中存在互感器,或者压控电压源或压控电流源的时候,电路中存在了耦合,
Z
Z
Z不再是对角阵
同时也没有限制 Z Z Z中元素一定为实数,在存在电抗器件的交流电路中, Z Z Z将变成一个复矩阵。
此外阻抗矩阵的逆矩阵被称为导纳矩阵 Y Y Y, i = Y u i=Yu i=Yu
再议回路
矩阵
G
G
G的左零空间
d
i
m
N
(
G
T
)
=
2
dim\ N(G^T)=2
dim N(GT)=2,这个值代表的是图中,线性无关的回路的数量
d
i
m
N
(
G
T
)
=
m
−
r
dim\ N(G^T)=m-r
dim N(GT)=m−r
代表着
#
l
o
o
p
s
=
#
e
d
g
e
s
−
(
#
n
o
d
e
s
−
1
)
\#loops=\#edges-(\#nodes-1)
#loops=#edges−(#nodes−1)
上式称为
E
u
l
e
r
′
s
f
o
r
m
u
l
a
Euler's\ formula
Euler′s formula
外部电源
电路中都会有外部电源,外部电源体现在什么地方?
对于电压源不难发现,体现在矩阵方程
G
ϕ
=
u
G\phi=u
Gϕ=u中
如果存在电流源,矩阵方程
G
T
i
=
f
G^Ti=f
GTi=f,
f
f
f将不再为0,因为有电流从某节点流入从某节点流出,看起来就好像存在着源点和阱点,但是注意,电流源从一个节点拉出的电流和从另一个节点灌入的电流必须相等,这意味着
f
f
f中所有元素之和一定是0。
电路理论的三个核心方程
u
=
G
ϕ
u=G\phi
u=Gϕ
G
T
i
=
f
G^Ti=f
GTi=f
u
=
Z
i
o
r
i
=
Y
u
u=Zi\ or\ i=Yu
u=Zi or i=Yu
将三个方程整合
G
T
Y
G
ϕ
=
f
G^TYG\phi=f
GTYGϕ=f
上式是稳态的数学问题的核心方程。
一阶差分方程
u
k
+
1
=
A
u
k
,
u
0
i
s
k
n
o
w
n
.
u_{k+1}=Au_k,u_0\ is\ known.
uk+1=Auk,u0 is known.
对角化
A
A
A
u
k
=
A
k
u
0
u_k=A^ku_0
uk=Aku0
设
A
A
A的特征向量分别为
x
1
,
x
2
⋯
x
n
x_1,x_2\cdots x_n
x1,x2⋯xn
将
u
0
u_0
u0使用特征向量线性表示
u
0
=
c
1
x
1
+
c
2
x
2
+
⋯
+
c
n
x
n
u_0=c_1x_1+c_2x_2+\cdots+c_nx_n
u0=c1x1+c2x2+⋯+cnxn
则
A
u
0
=
c
1
λ
1
x
1
+
c
1
λ
2
x
2
+
⋯
+
c
1
λ
n
x
n
Au_0=c_1\lambda_1x_1+c_1\lambda_2x_2+\cdots+c_1\lambda_nx_n
Au0=c1λ1x1+c1λ2x2+⋯+c1λnxn
A
k
u
0
=
c
1
λ
1
k
x
1
+
c
1
λ
2
k
x
2
+
⋯
+
c
1
λ
n
k
x
n
A^ku_0=c_1\lambda^k_1x_1+c_1\lambda^k_2x_2+\cdots+c_1\lambda^k_nx_n
Aku0=c1λ1kx1+c1λ2kx2+⋯+c1λnkxn
u
k
=
A
k
u
0
=
Λ
k
S
c
u_k=A^ku_0=\Lambda^kSc
uk=Aku0=ΛkSc
例子
F
i
b
o
n
a
c
c
i
Fibonacci
Fibonacci数列
F
k
+
1
=
F
k
+
F
k
−
1
,
F
0
=
0
,
F
1
=
1
F_{k+1}=F_k+F_{k-1},F_0=0,F_1=1
Fk+1=Fk+Fk−1,F0=0,F1=1
令
u
k
=
[
F
k
+
1
F
k
]
T
u_k=[F_{k+1}\ F_{k}]^T
uk=[Fk+1 Fk]T
u
k
+
1
=
[
1
1
1
0
]
u
k
,
u
0
=
[
1
0
]
u_{k+1}= \left[ \begin{matrix} 1&1\\ 1&0\\ \end{matrix} \right] u_k,u_0= \left[ \begin{matrix} 1\\ 0\\ \end{matrix} \right]
uk+1=[1110]uk,u0=[10]
特征值
λ
1
=
1
2
(
1
+
5
)
≈
1.618
,
λ
2
=
1
2
(
1
−
5
)
\lambda_1=\frac{1}{2}(1+\sqrt5)\approx1.618,\lambda_2=\frac{1}{2}(1-\sqrt5)
λ1=21(1+5)≈1.618,λ2=21(1−5)
这两个特征值的绝对值一个大于一,一个小于一,当
k
→
∞
k\rightarrow\infin
k→∞,
λ
2
k
→
0
\lambda_2^k\rightarrow0
λ2k→0,所以
u
k
=
λ
1
k
x
1
c
1
,
k
→
∞
u_k=\lambda_1^kx_1c_1,k\rightarrow \infin
uk=λ1kx1c1,k→∞
可以求得
x
1
=
[
λ
1
1
]
T
x_1=[\lambda_1\ 1]^T
x1=[λ1 1]T,
x
2
=
[
λ
2
1
]
T
x_2=[\lambda_2\ 1]^T
x2=[λ2 1]T
c
=
S
−
1
u
0
=
1
λ
1
−
λ
2
[
1
−
λ
2
−
1
λ
1
]
[
1
0
]
=
1
λ
1
−
λ
2
[
1
−
1
]
c=S^{-1}u_0= \frac{1}{\lambda_1-\lambda_2} \left[ \begin{matrix} 1&-\lambda_2\\ -1&\lambda_1\\ \end{matrix} \right] \left[ \begin{matrix} 1\\ 0\\ \end{matrix} \right]=\frac{1}{\lambda_1-\lambda_2} \left[ \begin{matrix} 1\\ -1\\ \end{matrix} \right]
c=S−1u0=λ1−λ21[1−1−λ2λ1][10]=λ1−λ21[1−1]
最后得到
u
k
=
1
5
[
1
2
(
5
+
1
)
]
k
[
1
2
(
5
+
1
)
1
]
,
k
→
∞
u_k=\frac{1}{\sqrt5}\left[{\frac{1}{2}(\sqrt5+1)}\right]^k \left[ \begin{matrix} {\frac{1}{2}(\sqrt5+1)}\\ 1\\ \end{matrix} \right] ,k\rightarrow \infin
uk=51[21(5+1)]k[21(5+1)1],k→∞
F
k
=
1
5
[
1
2
(
5
+
1
)
]
k
,
k
→
∞
F_k=\frac{1}{\sqrt5}\left[{\frac{1}{2}(\sqrt5+1)}\right]^k ,k\rightarrow \infin
Fk=51[21(5+1)]k,k→∞
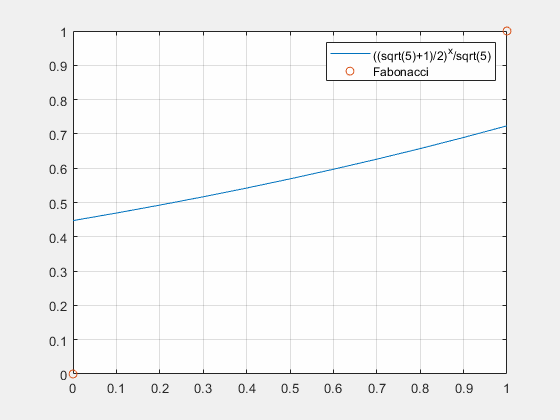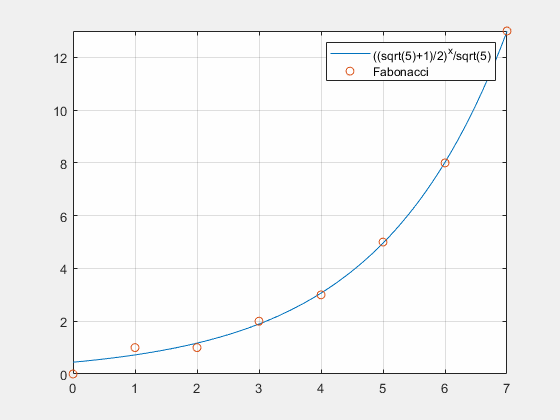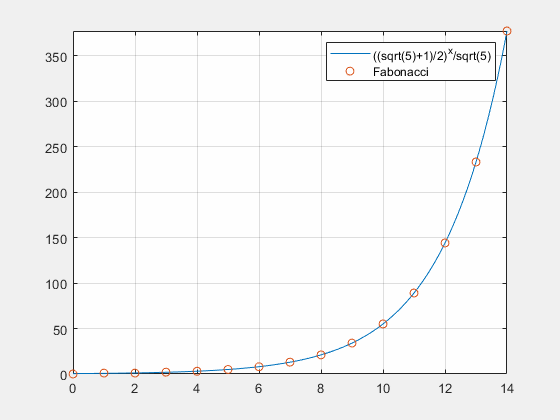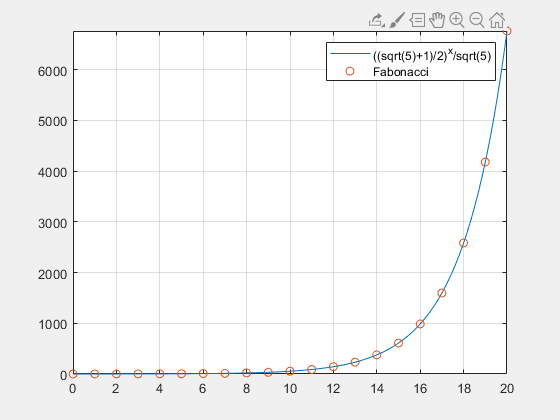

一阶常系数微分方程
d d t u 1 = − u 1 + 2 u 2 \frac{d}{dt}u_1=-u_1+2u_2 dtdu1=−u1+2u2
d
d
t
u
2
=
u
1
−
2
u
2
\frac{d}{dt}u_2=u_1-2u_2
dtdu2=u1−2u2
d
d
t
u
=
A
u
\frac{d}{dt}u=Au
dtdu=Au
A
=
[
−
1
2
1
−
2
]
,
u
=
[
u
1
u
2
]
A= \left[ \begin{matrix} -1&2\\ 1&-2 \end{matrix} \right], u=\left[ \begin{matrix} u_1\\ u_2 \end{matrix} \right]
A=[−112−2],u=[u1u2]
找到
A
A
A的特征值
λ
1
=
0
,
λ
2
=
−
3
\lambda_1=0,\lambda_2=-3
λ1=0,λ2=−3
特征向量
x
1
=
[
2
1
]
T
,
x
2
=
[
1
−
1
]
T
x_1=[2\ 1]^T,x_2=[1\ -1]^T
x1=[2 1]T,x2=[1 −1]T
解为
u
(
t
)
=
c
1
e
λ
1
t
x
1
+
c
2
e
λ
2
t
x
2
u(t)=c_1e^{\lambda_1t}x_1+c_2e^{\lambda_2t}x_2
u(t)=c1eλ1tx1+c2eλ2tx2
如果在一阶差分方程中,
A
A
A对应的解为
u
k
=
λ
1
k
x
1
c
1
+
λ
2
k
x
2
c
2
u_k=\lambda_1^kx_1c_1+\lambda_2^kx_2c_2
uk=λ1kx1c1+λ2kx2c2,两个式子一个是离散的一个是连续的
方程通解
u
=
c
1
[
2
1
]
+
c
2
e
−
3
t
[
1
−
1
]
u=c_1 \left[ \begin{matrix} 2\\ 1 \end{matrix} \right]+c_2e^{-3t} \left[ \begin{matrix} 1\\ -1 \end{matrix} \right]
u=c1[21]+c2e−3t[1−1]
c
1
c_1
c1和
c
2
c_2
c2是由初始条件决定的
假设初始条件是
u
(
0
)
=
[
1
0
]
T
u(0)=[1\ 0]^T
u(0)=[1 0]T
解得
c
1
=
c
2
=
1
/
3
c_1=c_2=1/3
c1=c2=1/3
最终解为
u
=
1
3
[
2
1
]
+
1
3
e
−
3
t
[
1
−
1
]
u=\frac{1}{3} \left[ \begin{matrix} 2\\ 1 \end{matrix} \right]+\frac{1}{3}e^{-3t} \left[ \begin{matrix} 1\\ -1 \end{matrix} \right]
u=31[21]+31e−3t[1−1]
u
(
∞
)
=
1
3
[
2
1
]
u(\infin)=\frac{1}{3} \left[ \begin{matrix} 2\\ 1 \end{matrix} \right]
u(∞)=31[21]为稳定状态
特征值与稳定性
-
s
t
a
b
i
l
i
t
y
:
a
l
l
r
e
a
l
p
a
r
t
s
o
f
e
i
g
e
n
v
a
l
u
e
s
a
r
e
n
e
g
a
t
i
v
e
.
stability:all\ real\ parts\ of\ eigenvalues\ are\ negative.
stability:all real parts of eigenvalues are negative.

那假如说特征值的虚部大于零会怎么样,假设有函数 y = e ( − 2 + 6 i ) t y=e^{(-2+6i)t} y=e(−2+6i)t,取其模,发现 ∣ y ∣ = e − 2 t |y|=e^{-2t} ∣y∣=e−2t,依然收敛,那么虚部有什么作用。
答案是震荡,虚部越大,震荡越剧烈

- h a s s t e a d y s t a t e : λ 1 = 0 , a n d t h e o t h e r e i g e n v a l u e s ′ r e a l p a r t s a r e n e g a t i v e . has\ steady\ state:\lambda_1=0,and\ the\ other\ eigenvalues'\ real\ parts\ are\ negative. has steady state:λ1=0,and the other eigenvalues′ real parts are negative.

-
b
l
o
w
u
p
:
i
f
a
n
y
e
i
g
e
n
v
a
l
u
e
′
s
r
e
a
l
p
a
r
t
i
s
p
o
s
i
t
i
v
e
.
blow\ up:\ if\ any\ eigenvalue's\ real\ part\ is\ positive.
blow up: if any eigenvalue′s real part is positive.

2 b y 2 2\ by\ 2 2 by 2
二阶的系数矩阵
[
a
b
c
d
]
\left[ \begin{matrix} a&b\\ c&d\\ \end{matrix} \right]
[acbd]
解要想稳定必须有
R
e
{
λ
1
}
<
0
,
R
e
{
λ
2
}
<
0
Re\{\lambda_1\}<0,Re\{\lambda_2\}<0
Re{λ1}<0,Re{λ2}<0
那么
t
r
a
c
e
=
a
+
d
<
0
trace=a+d<0
trace=a+d<0,并且
d
e
t
A
>
0
det\ A>0
det A>0
解耦与对角化
由于
A
A
A不是对角阵,所以
d
d
t
u
=
A
u
\frac{d}{dt}u=Au
dtdu=Au中的
u
1
u_1
u1和
u
2
u_2
u2是耦合的,要想解耦,需要对
A
A
A进行对角化。
令
u
=
S
v
u=Sv
u=Sv.,
S
S
S是
A
A
A的特征向量矩阵
S
d
d
t
v
=
A
S
v
S\frac{d}{dt}v=ASv
Sdtdv=ASv
d
d
t
v
=
S
−
1
A
S
v
=
Λ
v
\frac{d}{dt}v=S^{-1}ASv=\Lambda v
dtdv=S−1ASv=Λv
方程化为
d
d
t
v
=
Λ
v
\frac{d}{dt}v=\Lambda v
dtdv=Λv
解为
v
(
t
)
=
e
Λ
t
v
(
0
)
v(t)=e^{\Lambda t}v(0)
v(t)=eΛtv(0)
u
(
t
)
=
e
A
t
=
S
e
Λ
t
S
−
1
v
(
0
)
u(t)=e^{At}=Se^{\Lambda t}S^{-1}v(0)
u(t)=eAt=SeΛtS−1v(0)
M a t r i x e x p o n e n t i a l u = e A t u ( 0 ) Matrix\ exponential\ u=e^{At}u(0) Matrix exponential u=eAtu(0)
微积分中知道
y
=
e
x
y=e^x
y=ex的幂级数展开为
e
x
=
∑
i
=
0
∞
1
i
!
x
i
e^x=\sum\limits_{i=0}^\infin \frac{1}{i!}x^i
ex=i=0∑∞i!1xi
而矩阵指数为
e
A
t
=
∑
i
=
0
∞
1
i
!
(
A
t
)
i
,
(
A
t
)
0
=
I
e^{At}=\sum\limits_{i=0}^\infin \frac{1}{i!}(At)^i,(At)^0=I
eAt=i=0∑∞i!1(At)i,(At)0=I
再有幂级数
∑
i
=
0
∞
x
i
=
1
1
−
x
,
x
∈
(
−
∞
,
1
)
\sum\limits_{i=0}^\infin x^i=\frac{1}{1-x},x\in (-\infin,1)
i=0∑∞xi=1−x1,x∈(−∞,1)
则
∑
i
=
0
∞
(
A
t
)
i
=
(
I
−
A
t
)
−
1
\sum\limits_{i=0}^\infin (At)^i=(I-At)^{-1}
i=0∑∞(At)i=(I−At)−1
如果
A
t
At
At有特征值大于等于1,那么级数将不收敛
回到方程中
u
(
t
)
=
e
A
t
=
∑
i
=
0
∞
1
i
!
(
A
t
)
i
=
∑
i
=
0
∞
1
i
!
(
S
Λ
S
−
1
)
i
t
i
=
S
(
∑
i
=
0
∞
1
i
!
(
Λ
t
)
i
t
i
)
S
−
1
=
S
e
Λ
t
S
−
1
v
(
0
)
u(t)=e^{At}=\sum\limits_{i=0}^\infin \frac{1}{i!}(At)^i=\sum\limits_{i=0}^\infin \frac{1}{i!}(S\Lambda S^{-1})^i\ t^i=S\left(\sum\limits_{i=0}^\infin \frac{1}{i!}(\Lambda t )^i\ t^i\right)S^{-1}=Se^{\Lambda t}S^{-1}v(0)
u(t)=eAt=i=0∑∞i!1(At)i=i=0∑∞i!1(SΛS−1)i ti=S(i=0∑∞i!1(Λt)i ti)S−1=SeΛtS−1v(0)
当指数矩阵是对角矩阵的时候
e
Λ
t
=
[
e
λ
1
e
λ
2
t
⋱
e
λ
n
t
]
e^{\Lambda t}=\left[ \begin{matrix} e^{\lambda_1}&&&\\ &e^{\lambda_2t}&&\\ &&\ddots&\\ &&&e^{\lambda_nt}\\ \end{matrix} \right]
eΛt=⎣⎢⎢⎡eλ1eλ2t⋱eλnt⎦⎥⎥⎤
可以看出,只要有
R
e
{
λ
}
Re\{\lambda\}
Re{λ}大于0,解将不会收敛

浅谈二阶线性微分方程
y
′
′
+
b
y
′
+
k
y
=
0
y''+by'+ky=0
y′′+by′+ky=0
如何将上述方程化为一阶
令
u
=
[
y
′
y
]
T
u=[y'\ y]^T
u=[y′ y]T
则方程化为
u
′
=
[
−
b
−
k
1
0
]
u
u'=\left[ \begin{matrix} -b&-k\\ 1&0 \end{matrix} \right] u
u′=[−b1−k0]u
进而,如果有
n
n
n阶线性微分方程,那么就可以把其化为
n
n
n个一阶线性微分方程。
M a r k o v Markov Markov模型
M a r k o v Markov Markov矩阵
M a r k o v Markov Markov矩阵有三个特点
- 方阵
- 各列元素和为1
- 所有元素非负
P
=
[
0.1
0.01
0.3
0.2
0.99
0.3
0.7
0
0.4
]
P=\left[ \begin{matrix} 0.1&0.01&0.3\\ 0.2&0.99&0.3\\ 0.7&0&0.4\\ \end{matrix} \right]
P=⎣⎡0.10.20.70.010.9900.30.30.4⎦⎤
P
n
P^n
Pn也是
M
a
r
k
o
v
Markov
Markov矩阵
稳态问题
考虑 P P P的特征值
P P P一定会有一个特征值 λ = 1 \lambda=1 λ=1,而其他特征值的绝对值一定小于1。
在差分方程
π
k
=
P
k
π
0
=
Λ
k
S
c
\pi_k=P^k\pi_0=\Lambda^k Sc
πk=Pkπ0=ΛkSc中,当
k
→
∞
k\rightarrow\infin
k→∞时,只有
λ
=
1
\lambda=1
λ=1的项被保留下来了。
π
∞
=
c
1
x
1
\pi_{\infin}=c_1x_1
π∞=c1x1
x
1
x_1
x1中元素不会有负值
计算
P
−
I
P-I
P−I
P
−
I
=
[
−
0.9
0.01
0.3
0.2
−
0.01
0.3
−
0.7
0
−
0.6
]
P-I= \left[ \begin{matrix} -0.9&0.01&0.3\\ 0.2&-0.01&0.3\\ -0.7&0&-0.6\\ \end{matrix} \right]
P−I=⎣⎡−0.90.2−0.70.01−0.0100.30.3−0.6⎦⎤
可以发现矩阵各列和为0,所以其行列式一定为0,所以必有特征值1的特性得证
通过计算可知,
λ
=
1
\lambda=1
λ=1的特征向量是
[
0.6
33
0.7
]
T
[0.6\ 33\ 0.7]^T
[0.6 33 0.7]T
实例
考虑两个州:加州和麻省的人口问题,假设人口只会在这两个州之间迁移,每年有
90
%
90\%
90%的加州居民留在加州
10
%
10\%
10%的加州居民迁至麻省
20
%
20\%
20%的麻省居民迁至加州
80
%
80\%
80%的麻省居民留在麻省
设
u
k
=
[
u
c
a
l
u
m
a
s
s
]
T
u_k=[u_{cal}\ u_{mass}]^T
uk=[ucal umass]T代表了第
k
k
k年之后,两州的人数
于是有矩阵方程
u
k
+
1
=
A
u
k
u_{k+1}=Au_{k}
uk+1=Auk
A
=
[
0.9
0.2
0.1
0.8
]
A= \left[ \begin{matrix} 0.9&0.2\\ 0.1&0.8\\ \end{matrix} \right]
A=[0.90.10.20.8]
初始状态
u
0
=
[
0
1000
]
T
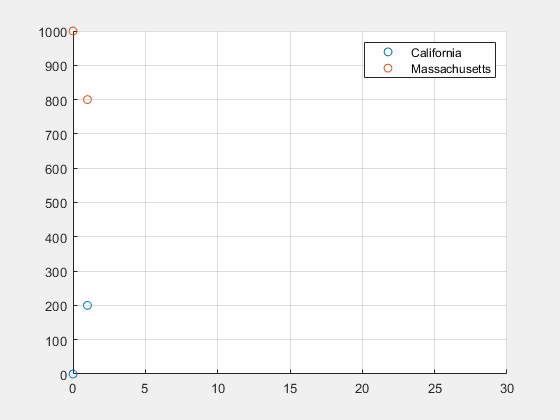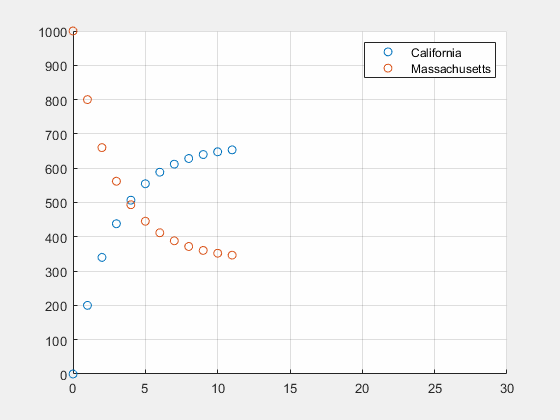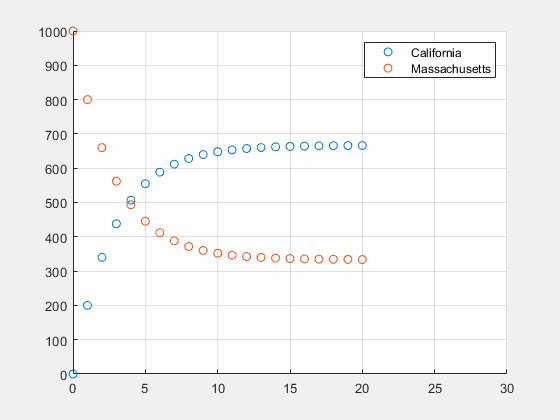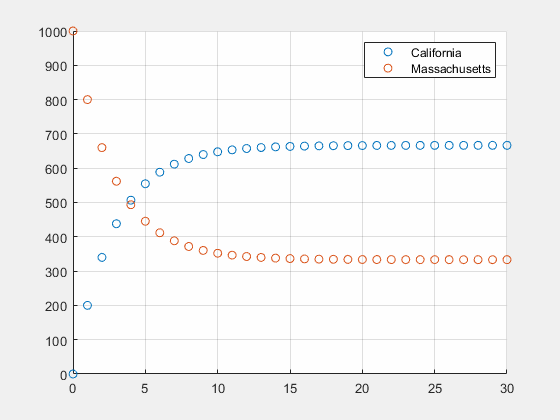
u_0=[0\ 1000]^T
u0=[0 1000]T
A
A
A的特征值
λ
1
=
1
\lambda_1=1
λ1=1,其特征向量是
[
2
1
]
T
[2\ 1]^T
[2 1]T,另一个特征值是
0.7
0.7
0.7,并不重要,这个特征值就是稳态,经过足够长时间加州的人口数将是麻省的2倍。
A
∞
=
[
2
/
3
2
/
3
1
/
3
1
/
3
]
A_\infin=\left[ \begin{matrix} 2/3&2/3\\ 1/3&1/3 \end{matrix} \right]
A∞=[2/31/32/31/3]
M a r k o v Markov Markov模型是一种概率模型,可以用一阶差分方程 π k + 1 = P π k \pi_{k+1}=P\pi_k πk+1=Pπk描述,每一个状态 π k \pi_k πk只与上一个状态 π k − 1 \pi_{k-1} πk−1有关。
傅里叶级数
有单位正交基的投影矩阵
有投影矩阵
Q
=
[
q
1
q
2
⋯
q
n
]
,
Q
T
Q
=
I
Q=[q_1\ q_2\cdots q_n],Q^TQ=I
Q=[q1 q2⋯qn],QTQ=I
有向量
v
=
x
1
q
1
+
x
2
q
2
+
⋯
+
x
n
q
n
v=x_1q_1+x_2q_2+\cdots+x_nq_n
v=x1q1+x2q2+⋯+xnqn
x
=
Q
T
v
x=Q^Tv
x=QTv
可以发现
q
i
T
v
=
x
i
q_i^Tv=x_i
qiTv=xi
傅里叶级数展开
f ( x ) = a 0 + a 1 c o s x + b 1 s i n x + a 2 c o s 2 x + b 2 s i n 2 x + ⋯ + a n c o n x + b n s i n n x + ⋯ f(x)=a_0+a_1cosx+b_1sinx+a_2cos2x+b_2sin2x+\cdots+a_nconx+b_nsinnx+\cdots f(x)=a0+a1cosx+b1sinx+a2cos2x+b2sin2x+⋯+anconx+bnsinnx+⋯
函数空间的正交
类比
v
T
w
=
∑
i
=
1
n
v
i
w
i
v^Tw=\sum\limits^n_{i=1}v_iw_i
vTw=i=1∑nviwi
f
T
g
(
x
)
=
∫
0
T
f
(
x
)
g
(
x
)
d
x
f^Tg(x)=\int^T_0f(x)g(x)dx
fTg(x)=∫0Tf(x)g(x)dx
上式为
f
(
x
)
f(x)
f(x)和
g
(
x
)
g(x)
g(x)的内积
如果
f
T
g
=
0
f^Tg=0
fTg=0称两函数正交
通过计算,会发现
{
s
i
n
i
x
,
c
o
s
i
x
∣
i
∈
N
}
\{sin\ ix, cos\ ix|i\in N\}
{sin ix,cos ix∣i∈N}是函数空间的正交基
傅里叶级数系数
如果将
c
o
s
n
x
cos\ nx
cos nx和
f
(
x
)
f(x)
f(x)做内积
∫
0
2
π
f
(
x
)
c
o
s
n
x
d
x
=
a
n
∫
0
2
π
c
o
s
2
n
x
d
x
=
a
n
π
\int_0^{2\pi}f(x)cos\ nx\ dx=a_n\int_0^{2\pi}cos^2\ nx\ dx=a_n\pi
∫02πf(x)cos nx dx=an∫02πcos2 nx dx=anπ
a
n
=
1
π
∫
0
2
π
f
(
x
)
c
o
s
n
x
d
x
a_n=\frac{1}{\pi}\int_0^{2\pi}f(x)cos\ nx\ dx
an=π1∫02πf(x)cos nx dx
同理,
b
n
=
1
π
∫
0
2
π
f
(
x
)
s
i
n
n
x
d
x
b_n=\frac{1}{\pi}\int_0^{2\pi}f(x)sin\ nx\ dx
bn=π1∫02πf(x)sin nx dx
FFT
F
n
=
[
1
1
1
⋯
1
1
w
n
w
n
2
⋯
w
n
n
−
1
⋮
⋮
⋮
⋱
⋮
1
w
n
n
−
1
w
n
2
(
n
−
1
)
⋯
w
n
(
n
−
1
)
(
n
−
1
)
]
F_n= \left[ \begin{matrix} 1&1&1&\cdots&1\\ 1&w_n&w^2_n &\cdots&w^{n-1}_n\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ 1&w^{n-1}_n&w^{2(n-1)}_n&\cdots&w^{(n-1)(n-1)}_n\\ \end{matrix} \right]
Fn=⎣⎢⎢⎢⎡11⋮11wn⋮wnn−11wn2⋮wn2(n−1)⋯⋯⋱⋯1wnn−1⋮wn(n−1)(n−1)⎦⎥⎥⎥⎤
F
o
u
r
i
e
r
Fourier
Fourier矩阵有一个很好的性质,这种性质存在与
F
2
n
F_{2n}
F2n和
F
n
F_n
Fn之间,
w
2
n
2
=
w
n
w_{2n}^2=w_n
w2n2=wn
以
F
64
F_{64}
F64为例,假设
F
64
F_{64}
F64可以拆成对角线上是
F
32
F_{32}
F32的对角分块矩阵,引入两个修正矩阵对分块矩阵左乘和右乘。
F
64
=
[
M
]
[
F
32
O
O
F
32
]
[
P
]
F_{64}= \left[ \begin{matrix} & &M&&\\ &&&&\\ \end{matrix} \right] \left[ \begin{matrix} F_{32}&O\\ O&F_{32}\\ \end{matrix} \right] \left[ \begin{matrix} & &P&&\\ & &&&\\ \end{matrix} \right]
F64=[M][F32OOF32][P]
先计算一下计算开销,原来
F
64
F_{64}
F64对序列做离散傅里叶变换,需要
6
4
2
64^2
642次复数乘法和若干次复数加法,对
F
32
F_{32}
F32进行分解后,运算次数降为
2
(
3
2
2
)
+
f
i
x
u
p
2(32^2)+fix\ up
2(322)+fix up
接下来先考虑右乘矩阵,右乘矩阵实际上是一个置换矩阵,用于将序列重排,偶元素在前,奇元素后
以
P
8
P_8
P8为例
P
8
=
[
1
1
1
1
1
1
1
1
]
P_8= \left[ \begin{matrix} 1&&&&&&\\ &&1&&&&\\ &&&&1&&&\\ &&&&&&1&\\ &1&&&&&\\ &&&1&&&\\ &&&&&1&&\\ &&&&&&&1\\ \end{matrix} \right]
P8=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡11111111⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
P
8
x
=
[
1
1
1
1
1
1
1
1
]
[
x
0
x
1
x
2
x
3
x
4
x
5
x
6
x
7
]
=
[
x
0
x
2
x
4
x
6
x
1
x
3
x
5
x
7
]
=
[
x
e
v
e
n
x
o
d
d
]
P_8x= \left[ \begin{matrix} 1&&&&&&\\ &&1&&&&\\ &&&&1&&&\\ &&&&&&1&\\ &1&&&&&\\ &&&1&&&\\ &&&&&1&&\\ &&&&&&&1\\ \end{matrix} \right] \left[ \begin{matrix} x_0\\ x_1\\ x_2\\ x_3\\ x_4\\ x_5\\ x_6\\ x_7\\ \end{matrix} \right]= \left[ \begin{matrix} x_0\\ x_2\\ x_4\\ x_6\\ x_1\\ x_3\\ x_5\\ x_7\\ \end{matrix} \right]= \left[ \begin{matrix} x_{even}\\ x_{odd}\\ \end{matrix} \right]
P8x=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡11111111⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡x0x1x2x3x4x5x6x7⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡x0x2x4x6x1x3x5x7⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤=[xevenxodd]
在对序列进行奇偶排列后,分别对
x
e
v
e
n
x_{even}
xeven和
x
o
d
d
x_{odd}
xodd做离散傅里叶变换,然后将变换后的序列重新组合,这个合并操作,由
M
(
M
f
o
r
m
e
r
g
e
)
M(M\ for\ merge)
M(M for merge)来完成。
D
i
a
g
o
n
a
l
(
F
32
)
[
x
e
v
e
n
x
o
d
d
]
=
[
f
e
v
e
n
f
o
d
d
]
Diagonal(F_{32}) \left[ \begin{matrix} x_{even}\\ x_{odd}\\ \end{matrix} \right]= \left[ \begin{matrix} f_{even}\\ f_{odd}\\ \end{matrix} \right]
Diagonal(F32)[xevenxodd]=[fevenfodd]
[
M
]
[
f
e
v
e
n
f
o
d
d
]
=
f
\left[ \begin{matrix} & &M&&\\ &&&&\\ \end{matrix} \right] \left[ \begin{matrix} f_{even}\\ f_{odd}\\ \end{matrix} \right]=f
[M][fevenfodd]=f
M
M
M矩阵为
M
=
[
I
D
I
−
D
]
M= \left[ \begin{matrix} I&D\\ I&-D\\ \end{matrix} \right]
M=[IID−D]
无论是
I
I
I还是
P
P
P,在计算过程中都不需要太大开销,所以修正因子的计算开销主要由对角阵
D
D
D引入。总的计算开销为
2
(
3
2
2
)
+
32
2(32^2)+32
2(322)+32
最后
D
=
[
1
w
64
w
64
2
⋱
w
64
31
]
D= \left[ \begin{matrix} 1&&&&\\ &w_{64}&&&\\ &&w_{64}^2&&\\ &&&\ddots&\\ &&&&w_{64}^{31}\\ \end{matrix} \right]
D=⎣⎢⎢⎢⎢⎡1w64w642⋱w6431⎦⎥⎥⎥⎥⎤
显然主要开销还是由
F
32
F_{32}
F32引起,但是它可以被进一步分解,计算开销进一步下降为
2
[
2
(
16
)
2
+
16
]
+
32
2[2(16)^2+16]+32
2[2(16)2+16]+32,持续下去。
递归基
n
=
2
n=2
n=2,主要的递归式是
O
(
F
F
T
2
n
)
=
O
(
2
F
F
T
n
)
+
n
O(FFT_{2n})=O(2FFT_n)+n
O(FFT2n)=O(2FFTn)+n
递归基
O
(
F
F
T
2
)
=
4
O(FFT_2)=4
O(FFT2)=4
解得
O
(
F
F
T
n
)
≈
n
l
o
g
n
/
2
O(FFT_n)\approx nlogn/2
O(FFTn)≈nlogn/2
图像压缩
图像的计算机表示
一幅图像,由许多各像素点构成,一副分辨率为 m ∗ n m*n m∗n的的图像有 m ∗ n m*n m∗n个像素点。每个像素点有三个值 r e d , g r e e n , b l u e red,green, blue red,green,blue,这是众所周知的三原色,三种颜色不同强度的搭配,可以形成任何颜色,每个值是一个 1 B y t e 1\ Byte 1 Byte大小的值,范围从 0 0 0到 255 255 255,代表了对应颜色的强度。总而言之一幅图像是一个 m ∗ n ∗ 3 m*n*3 m∗n∗3的三维矩阵。
为什么要进行基变换
这里将问题简化为二维矩阵,即考虑某一个色彩的灰度值,其他几种颜色的压缩都是同理的,将一个像素的灰度值赋予一个1,作为标准基,所以整个图像会有
m
∗
n
m*n
m∗n个基(和矩阵空间的基一样,这里也是个矩阵,只有一个非零元)。
[
1
]
[
1
]
⋯
[
1
]
\left[ \begin{matrix} 1&&&\\ &&&\\ &&&\\ &&&\\ \end{matrix} \right] \left[ \begin{matrix} &1&&\\ &&&\\ &&&\\ &&&\\ \end{matrix} \right]\cdots \left[ \begin{matrix} &&&\\ &&&\\ &&&\\ &&&1\\ \end{matrix} \right]
⎣⎢⎢⎡1⎦⎥⎥⎤⎣⎢⎢⎡1⎦⎥⎥⎤⋯⎣⎢⎢⎡1⎦⎥⎥⎤
为什么要进行基变换?因为如果直接抛弃标准基中某分量的信息,那么会在图像中造成黑点,这当然不是很好的有损压缩,好的有损压缩是在尽力保证图像品质的同时,缩小图像的体积。
以下为了便于分析,将矩阵基视为向量,一个
m
∗
n
m*n
m∗n维的向量。
实际中的压缩算法都是将图像矩阵分块,JPEG将图像矩阵分块为若干
8
∗
8
8*8
8∗8的小块。
什么样的基是合适的
- 计算迅速,进行基变换的速度要快
- 良好的压缩性,少量的基就可以接近信号
傅里叶基
傅里叶基是由离散傅里叶变换得到的,不同的基代表着不同频率的序列
,频率最低的基是
[
1
1
⋯
1
]
T
[1\ 1\cdots 1]^T
[1 1⋯1]T,频率最高的基是
[
1
−
1
⋯
1
−
1
]
T
[1\ -1\cdots\ 1\ -1]^T
[1 −1⋯ 1 −1]T。
在对序列进行 D F T DFT DFT后,丢掉一些不重要的,值很小的分量,解码再做 I D F T IDFT IDFT,恢复成标准基。此称为阈值量化。往往高频信号的系数会比较小,一般滤掉的是高频信号
小波基
R
8
\mathbb R^8
R8空间中的小波基
[
1
1
1
1
1
1
1
1
]
[
1
1
1
1
−
1
−
1
−
1
−
1
]
[
1
1
−
1
−
1
0
0
0
0
]
[
0
0
0
0
1
1
−
1
−
1
]
[
1
−
1
0
0
0
0
0
0
]
[
0
0
1
−
1
0
0
0
0
]
[
0
0
0
0
1
−
1
0
0
]
[
0
0
0
0
0
0
1
−
1
]
\left[ \begin{matrix} 1\\ 1\\ 1\\ 1\\ 1\\ 1\\ 1\\ 1\\ \end{matrix} \right] \left[ \begin{matrix} 1\\ 1\\ 1\\ 1\\ -1\\ -1\\ -1\\ -1\\ \end{matrix} \right] \left[ \begin{matrix} 1\\ 1\\ -1\\ -1\\ 0\\ 0\\ 0\\ 0\\ \end{matrix} \right] \left[ \begin{matrix} 0\\ 0\\ 0\\ 0\\ 1\\ 1\\ -1\\ -1\\ \end{matrix} \right] \left[ \begin{matrix} 1\\ -1\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ \end{matrix} \right] \left[ \begin{matrix} 0\\ 0\\ 1\\ -1\\ 0\\ 0\\ 0\\ 0\\ \end{matrix} \right] \left[ \begin{matrix} 0\\ 0\\ 0\\ 0\\ 1\\ -1\\ 0\\ 0\\ \end{matrix} \right] \left[ \begin{matrix} 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 1\\ -1\\ \end{matrix} \right]
⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡11111111⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡1111−1−1−1−1⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡11−1−10000⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡000011−1−1⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡1−1000000⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡001−10000⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡00001−100⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡0000001−1⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
将某八像素图像表示成
p
=
c
1
w
1
+
c
2
w
2
+
⋯
+
c
8
w
8
p=c_1w_1+c_2w_2+\cdots+c_8w_8
p=c1w1+c2w2+⋯+c8w8
p
=
[
w
1
w
2
⋯
w
8
]
c
p=[w_1\ w_2\cdots w_8]c
p=[w1 w2⋯w8]c
p
=
W
c
p=Wc
p=Wc
基变换的关键在于解上述方程
c
=
W
−
1
p
c=W^{-1}p
c=W−1p
求解方程其实也有和
F
F
T
FFT
FFT类似的快速算法称为快速小波变换
可以观察到,矩阵
W
W
W是正交矩阵,虽然不是标准正交矩阵,但是一个常数因子不影响算法思想,通过转置和少量修正可以很快得到
W
−
1
W^{-1}
W−1
























 584
584

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








