凸函数的四个定义
定义一
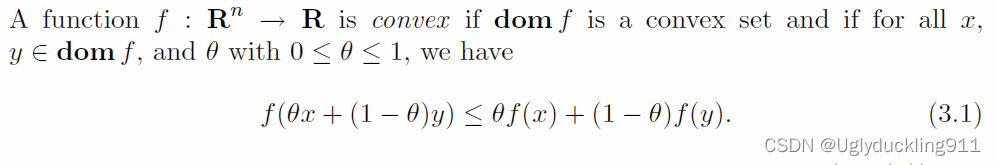
其中 dom f f f 是函数 f f f 的 定义域（前域），为凸集——这个很重要，后面的一些定义中也会用到，甚至对于凹函数也是。
从几何意义上来说，（3.1）意味着曲线上，从
x
x
x 到
y
y
y 的弦，在函数
f
f
f 的图像上方。
若
x
x
x 和
y
y
y 不相等，且
0
<
θ
<
1
0<\theta<1
0<θ<1 ,称该函数
f
f
f 是严格凸的
tip
- f f f 为凸， − f -f −f 为凹函数
- f f f 为严格凸， − f -f −f 为严格凹函数
- 所有仿射函数为既凸又凹的；反之，某个函数为既凸又凹的，则为仿射函数
定义二
函数是凸函数，当且仅当其在与其定义域相交的任何直线上都是凸的。
换言之，函数
f
f
f 是凸的，当且仅当对于任意
x
∈
x\in
x∈dom
f
f
f 和任意向量
v
v
v，
函数
g
(
t
)
=
f
(
x
+
t
v
)
g(t)=f(x+tv)
g(t)=f(x+tv) 是凸的（其定义域为{
t
∣
x
+
t
v
∈
t|x+tv\in
t∣x+tv∈dom
f
f
f}）
该性质容许我们通过将函数限制在直线上判断其是否为凸函数；
也可以说这个定义将原高维空间降到了一维空间。
定义三
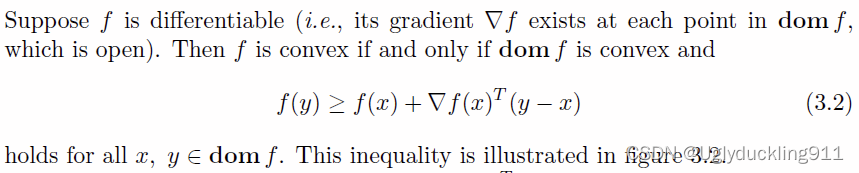
此处假设
f
f
f 可微，dom
f
f
f 为凸集和任意
x
,
y
∈
x,y\in
x,y∈dom
f
f
f 满足（3.2）不等式，则说明函数
f
f
f 为凸函数。
该定义也可称为凸函数的一阶条件
用二维曲线，可以比较直观的说明相互关系。
定义四
假设
f
f
f 二阶可微，对于开集dom
f
f
f内的任意一点，它的Hessian矩阵或二阶导数存在，则函数
f
f
f 为凸函数的充要条件是，Hessian矩阵是半正定阵。
当对于R上的函数，可以简化为条件
f
′
′
(
x
)
≥
0
f''(x)\ge0
f′′(x)≥0 (当然此时依然需要满足dom
f
f
f是凸的，即一个区间)。
该定义也可称为凸函数的二阶条件。
类似的，函数 f f f 是凹函数的充要条件是，dom f f f 是凸集且对于任意 x ∈ x\in x∈dom f f f， ∇ 2 f ( x ) ⪯ 0 \nabla^2f(x)\preceq0 ∇2f(x)⪯0
一些栗子
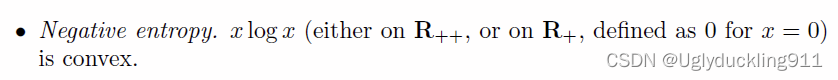
指数和的对数为凸函数的证明如下：
几何平均的函数为凹函数的证明如下：（个人的方法）
可将上图大的矩阵设为U
即证明U为正定矩阵即可，
即证明：任意矩阵V，
V
T
U
V
≥
0
V^TUV\ge0
VTUV≥0
上式可化简如下
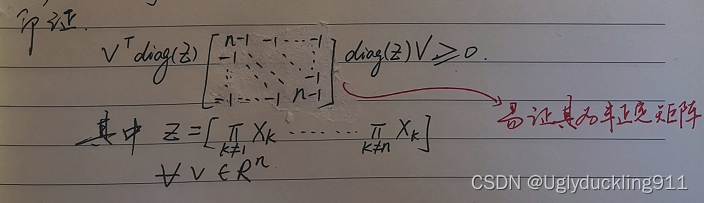
教材里的方法：
1543
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
