算法：轮廓线dp

什么是轮廓线DP

• 适用范围: 较窄的棋盘($m\times n$中$m$或者$n$较小)。按整行或者整列无法进行转态转移。而把轮廓线作为状态一部分。具体见例题。

例题一：铺砖问题(Poj 2411)

我们在状压DP中已经介绍过一种整行状态转移的方法，但是这里我们采用轮廓线的方法解决。对每个小格，我们定义0为非覆盖，1为覆盖。
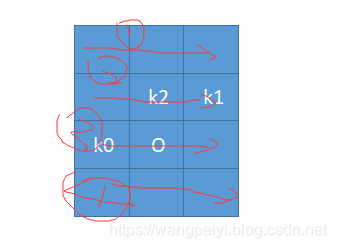
对每一个小格，其轮廓线包含了该小格和(1) 该小格前面，且 (2)确定该小格后状态还不确定的小格。如图红色框所示。(因为前面的其他小格必定已经全部铺满了，因此不必再考虑)

因此对每个小格对应的轮廓线里的小格，考虑不确定性，共有 $2^m$ 个状态。因此对每个小格，我们需要分配$2^m$个状态。因此:

• 定义dp$[cur][S]$: 当前所讨论小格轮廓线内状态为$S$时(例子中$S={k_1{k}_{0}O}_{(2进制)}$，当前小格和当前小格前面所有小格组成区域（绿色圈内区域）的总共铺放方法数。
• 目标状态：$dp[last][2^m-1]$。
• 状态转移:
  • 选择：对每个小格，由于我们只讨论其对前面区域的影响，故可以选择(1): 不放。(2):左放。(3):上放。
    • 不放: (1): $O=0$,，(2)前一状态的$k_2$为1
    • 左放: (1): 当前小格不在第一列。（2):$k_0=O=1$。(3):前一状态的$k_0=0，k_2=1$
    • 上放: (1): 当前小格不在第一排。(2): $O=1$。 (3): 前一状态的$k_2=0$
      
      这里不铺和其余两种状态是互斥的。
  • 滚动数组：当前小格是在前一个小格的基础上讨论，故采用滚动数组。用:
    • $dp[x][S]$: 表示前一个小格的状态。
    • $dp[1-x][S]$: 表示后一个小格的状态。 x ∈ { 0 , 1 } . x \in \{0, 1\}. x∈{0,1}.
  • 根据转移的选择以及条件，有状态转移方程式:
    $$\begin{array}{rl}A& =dp[1-cur][(s>>1)|(1<<(m-1))]\\ B& =dp[1-cur][((s>>1)|(1<<(m-1)))\&((1<<m)-2)]\\ C& =dp[1-cur][s>>1]\end{array}$$
    $$dp[cur][S]=\{\begin{array}{ll}A& 当前S满足不铺条件\\ B& 当前S满足左铺条件\\ C& 当前S满足上铺条件\\ B+C& 当前S满足左铺和上铺条件\end{array}$$
    这里A对应不放，B对应左放，C对应上放的前一小格对应状态数量。
• 更新策略: 二维数组循环遍历更新
  
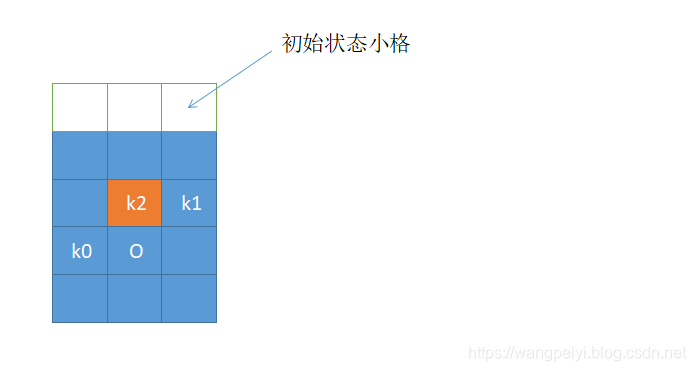
• 初始状态: $dp[0][2^m-1]$ = 1，其余为0。(这里人为想象一个第0排，由于第一排不能上放，因此第0排需要全为1， 初始状态对应的是假想第0排的最后一个小格)

• AC代码:

#include<iostream>
#include<cstring>
using namespace std;

int m, n;
const int MAX = 1 << 13;
typedef long long ll;
ll dp[2][MAX];
int main()
{
    int cur;
    while(cin >> m >> n)
    {
        if(m + n == 0)
            return 0;
        if(n < m)
            swap(n, m);
        memset(dp,0,sizeof(dp));
        cur = 0;
        dp[cur][(1<<m)-1] = 1;
        for(int i=0; i<n; i++)
        {
            for(int j=0; j<m; j++)
            {
                cur ^= 1;
                memset(dp[cur], 0, sizeof(dp[cur]));
                for(int s=0; s<(1<<m); s++)
                {
                    // 不放
                    if(!(s&1))
                        dp[cur][s] += dp[1-cur][(s>>1) | (1 << (m-1))];
                    else
                    {
                        // 左放
                        if(j && (s >> 1 & 1))
                            dp[cur][s] += dp[1-cur][((s >> 1) | (1 << (m-1))) & ((1<<m)-2)];
                        // 上放
                        if(i)
                            dp[cur][s] += dp[1-cur][s >> 1];
                    }

                }
            }
        }
        cout << dp[cur][(1<<m)-1] << endl;
    }
}

例题二：铺砖问题(挑战程序设计竞赛P196）

• 题意:
  
• 思路:
  可以看到，这道题中加入了黑色砖不用铺，也不能够铺的限制。我们遵循例题一同样的思路，但是我们认为黑色砖衡为被覆盖，其值永远1。当我们对一个状态$dp[cur][S]$进行讨论时。
• 若该状态对应小格为黑砖。
  • 若$S\&1=0$: 那么不可能存在这样的状态，自然$dp[cur][S]=0$(当前讨论状态所在小格的覆盖情况是$S$的最后一位,而我们把黑砖作为衡为1的覆盖)
  • 若$S\&1=1$: 由于该小格不能铺砖，因此上方小格已经铺好。
    
• 若该状态对应的小格不是黑砖，可以选择。
  • 不放: (1): $O=0$,，(2)前一状态的$k_2$为1
  • 左放: (1): 当前小格不在第一列。（2):$k_0=O=1$。(3):前一状态的$k_0=0，k_2=1$。(4): 左边的小格不可以是黑砖。
  • 上放: (1): 当前小格不在第一排。(2): $O=1$。 (3): 前一状态的$k_2=0$。(4): 上面的小格不可以是黑砖。

#include<iostream>
#include<cstring>
using namespace std;

int m, n;
const int MAX = 1 << 13;
typedef long long ll;
ll dp[2][MAX];
char color[MAX][MAX];
int main()
{
    int cur;
    while(cin >> n >> m)
    {
        for(int i=0; i<n; i++)
        {
            for(int j=0; j<m; j++)
            {
                cin >> color[i][j];
            }
        }
        memset(dp,0,sizeof(dp));
        cur = 0;
        dp[cur][(1<<m)-1] = 1;
        for(int i=0; i<n; i++)
        {
            for(int j=0; j<m; j++)
            {
                cur ^= 1;
                memset(dp[cur], 0, sizeof(dp[cur]));
                for(int s=0; s<(1<<m); s++)
                {
                    // --------------------加入代码--------------------------------
                    if(color[i][j] == 'x')
                    {
                    	/*如果当前格为黑色，那么该轮廓线最后一个2进制位只能为1。
                    	按状态定义，若最后2进制位为0，则铺法为0.
                    	*/
                        if(!(s&1))
                            dp[cur][s] = 0;
                        /*如果当前格为黑色，且轮廓线最后一个2进制位1，则上方一个格子只能为1*/。
                        else
                            dp[cur][s] += dp[1-cur][(s>>1) | (1 << (m-1))];

                    }
                    // -----------------------------------------------------------------
                    else
                    {
                        // 不放
                        if(!(s&1))
                            dp[cur][s] += dp[1-cur][(s>>1) | (1 << (m-1))];
                        else
                        {
                        	// --------------------------增加限制条件----------------------------//
                            	// 左放
                            if(j && (s >> 1 & 1) && color[i][j-1]!='x')
                                dp[cur][s | 3] += dp[1-cur][((s >> 1) | (1 << (m-1))) & ((1<<m)-2)];
                            	// 上放
                            if(i && color[i-1][j] != 'x')
                                dp[cur][s] += dp[1-cur][s >> 1];
                           // -------------------------------------------------------------------------//
                        }
                    }

                }
            }
        }
        cout << dp[cur][(1<<m)-1] << endl;
    }
}