【非线性连续介质力学】文献综述

【非线性连续介质力学】文献综述

本文翻译自新南威尔士大学O’Shea, Daniel的博士论文的文献综述部分：Hyperelasticity for soft biological tissues and fibre-reinforced composites using orthotropic fourth-order tensors

0. 简介

本文重点关注非线性连续介质力学的研究现状，特别是各向异性体。

本文将按照时间顺序详细说明连续介质力学的历史起源，在力学领域的发展和演变，以及过程中催生出来的能够预测纤维增强复合材料和软生物组织高度非线性力学响应的数学和计算工具。对经典力学原理和非线性弹性力学知识的学习有助于理解本文提出的正交各向异性超弹性建模和计算的动机和新颖之处。

拉格朗日、纳维、胡克、柯西和格林等人的工作，在有限运动学和热力学原理的发展中起到了重要作用，这些理论被广泛应用于描述非线性弹性材料行为。Eringen、Rivlin和Spencer等人在各向同性体上重点使用的是基于不变量来构建应变能函数，以此描述有限变形。然后，自然而然就推广到各向异性领域（方向相关），并且引入了结构张量的形式以及伪不变量作为数学工具。

基于唯象学理论的非线性连续介质力学，是通过拟合实验数据来获取和修正模型参数，并且在揭示定向微结构胶原纤维对软组织力学行为的影响中发挥了重要作用。总的来说，数学模型严格受到实验室数据的限制，并且一般只能专门用来描述特定的生物组织材料，而非适用于所有情况。

随着纤维增强复合材料的发展，航空航天、建筑、机器人、医疗植入和假肢等领域都依赖这些前沿领域的研究。然而，传统的数学方法在预测层压复合材料中复杂界面应力应变行为时，在计算中往往存在数值不稳定和不可靠性。

本文结尾，将会展示科学家们是如何在经典的科学工作的基础上，利用数学框架对正交各向异性可变形体进行表征的。这些技术将在理解人体器官和组织的复杂结构和工作原理中起到至关重要的作用。

1. 非线性连续介质力学历史

现代连续介质力学的语言是微分几何。这些工作来自于Leonhard Euler对一般曲面曲率的研究工作以及19世纪中叶Joseph Lagrange的著名著作《Analytique Méchanique》。

如今，弹性力学使用的微分方程是由纳维推出的，然而，现代工程师们所依赖的应力应变模型则是由柯西发展的，并提出了柯西的能量守恒定律和运动方程。

在这之前，对物体变形和作用力之间的关系的发现则是来自于罗伯特·胡克，并且他写下了一个拉丁短语：

“Ut tensio, sic vis”

意思是，张力与力相对应。这就是我们通常所说的胡克定律。

随后A.E.Love对其进行了解释：

“The power of any spring is in the same proportion with the tension thereof"

意思是，任何弹簧的力与其张力成正比。

线性化的现代连续介质力学其实是三维的广义胡克定律，最早将此广义胡克定律引入应力应变概念的是1827年的Augustin Cauchy。通过Cauchy的小应变张量 $ϵ$ ，可以描述运动学的线性化理论，而胡克定律则提供了与小应力 $\sigma$的三维刚度关系。

如今，用广义胡克定律描述的变形体被称为“柯西弹性体”。同样地，柯西引入了拉伸主值和应力主值等概念，这些概念都成为了表示应变能函数的基础。另外，一个叫Gabriel Lamé的数学家，通过考虑材料的对称性，提供了一个将描述各向同性体的参数减少为两个的方法，至今这两个参数仍以其名字命名，即拉梅系数。

对于某些硫化弹性体，其应力应变行为在大的荷载下表现出非线性行为，至此，胡克弹性体将不再适用。因此，亟需一种健壮的数学框架来应对这些问题。有关有限弹性变形的理论是由George Green在1839年提出的，他参考了光学领域，引入了格林-拉格朗日应变张量，这个张量至今在现代连续介质力学中仍在广泛使用。这个张量是直接从变形梯度张量推导得来的，并且可以在小变形上也适用胡克定律，这种在所有变形尺度上保持稳定性的特点是非线性公式的重要特点。通过忽略高阶项，可以很容易退化到柯西小应变张量。基于此，非线性运动学的描述以及应力响应，建立了非线性弹性材料的固体力学。

应力和非线性应变能函数的概念是将有限变形运动学和热力学原理融合进一个同一个力学框架的结果。Clifford Truesdell在1960年代建立了连续介质力学（从当今的理解来看），他的两部重要作品《Classical Field Theories》和《The Non-linear Field Theories of Mechanics》对非线性连续体力学进行广泛的概述和提供了详实的背景。

本构方程实际上是将应力测量和变形梯度联系起来，并且描述这个关系的函数被称为响应函数。这个响应函数表征了弹性材料的材料特性，确定给定的材料的响应函数需要对能量和热力学相关的量进行微分分析。

如果存在一个函数，这个函数是关于变形梯度可导的，那么这个材料被称为超弹性。这个导数返回的是与第一类皮奥拉-基尔霍夫应力相关联的响应函数，这就定义了所谓的应变能函数，是一种衡量连续体变形后所储存的能量。通常定义为单位体积，用 $\Psi$来表示。

应变能函数需要满足凸性和客观性条件，保证稳定性和可以得到物理解。客观性，或者说是不变性，是与能量的守恒相关的，可以确保一个热力学过程转换到另一个热力学过程。这也意味着应变能函数必须满足物质框架不变性原理，Clifford Truesdell定义如下：

“Constitutive equations involving thermodynamic and mechanical variables must be invariant under change of frame”

意思是，涉及热力学和力学变量的本构方程在框架变换下必须保持不变，这里的框架变换可以理解成改变观察者的视角。

物质框架不变性是任何本构方程都需要满足的本质特征。应变能通过将其表达成一些运动学张量的不变量的函数来满足物质框架不变性，其中最受欢迎的是来自Rivlin在《Large elastic deformations of isotropic materials》的重要工作。因此，基于不变量的超弹性因其数学上的简单自然而然地得到了关注，并且至今仍然是许多数学家的选择。

第二个需要满足的条件是凸性，是用来判断微分方程是否存在解的重要指标。对于给定边界条件的弹性力学问题，解通常是系统总能量的最小值。Holzapfel指出，解的存在性是基于应变能函数的多凸性条件。1976年John Ball在他的作品《Convexity conditions and existence theorems in nonlinear elasticity》详细阐述了多凸性的概念，他指出，解的存在性问题与寻找非线性弹性的令人满意的本构不等式问题是密不可分的。Itskov等人也解释道，多凸性意味着拟凸性，拟凸性又保证了椭圆性，从而满足了Legendre-Hadamard条件，而这又确保了连续体的总能量的全局最小是存在的。最近Neff的工作基于Cosserat brothers理论拓展了这个概念，证明了非经典微极体固体的最小是存在的。

各向同性Hookean材料的应变能函数表述如下：

$$\tilde{\Psi }=\frac{1}{2}(\lambda {\mathrm{tr}}^2(ϵ)+\mu \mathrm{tr}({ϵ}^2))$$
两个参数即上文提到的拉梅系数。

这种解耦形式将应变能分解成两个各向同性的二次函数，这种将应变能函数分解成两个不同的物理部分在工程中是很常见的。但是，Truesdell and Noll认为，Hookean应变能模型在超出小变形范围后没有物理意义，也就是不再满足物质框架不变性原理。这意味着，拉梅系数只能在柯西连续体使用。然而，Ciarlet认为，这只是个误解，并且给出了证明，即应变能的拉梅分解不局限于线性弹性体，还可以正确地适用于各向同性弹性体。

各向同性的概念反映的是连续体的响应函数不依赖任何叠加的刚体运动，任何不满足这个性质的材料，都被称为各向异性。对于给定材料在有限的一组变换下的响应函数的客观性可以决定其各向异性程度，可以归类到对称群，相关的重要工作可以参考Ogden或Truesdell and Noll的工作。在三维空间中，Spencer 定义了32种晶体类，每种晶体类都与其自己正交张量变换群相关。在连续介质力学中，比较有用的概念是对称性，例如，各向同性、横向各向同性和正交各向异性等材料特性分别具有零个、一个和两个偏爱方向，并且在正交各向异性的情况下，这两个偏爱方向是相互正交的。

同时，早期的很多连续介质力学工作都是基于各向同性材料的，但是，随着对生物组织或纤维增强复合材料的研究，理解这种具有偏爱方向的材料力学行为变得越来越重要，这推动了对各向异性行为的研究需求。

本文提出的模型必须尽可能满足上文提到的想法和条件，首先，需要有一个可以捕捉各向异性行为的模型；其次，当受到小应变作用时，对超弹性材料来说，应该可以保持胡克响应。Truesdell的物质框架不变性和Ball的凸性将成为我们所提出的模型的边界条件，以此来保证我们的弹性力学问题在任何变形尺度和任何程度的各向异性都能保证稳定。

有限变形的自然对数应变张量

对于有限变形，怎么描述运动学的测量其实是不简单，也不明显。Heinrich Hencky在他的工作中就有详细讨论，并给出对给定模型的有限应变张量的选择：

“At the foundation of all elasticity theories lies the definition of strain, and before introducing a new law of elasticity we must explain how finite strain is to be measured”

意思是，所有的弹性理论的基础依赖于应变的定义，在介绍一个新的弹性理论之前必须解释清楚有限应变是如何衡量的。

格林-拉格朗日应变张量，即欧拉-阿尔曼西应变张量是工程中使用最多的有限变形测量，因为它们直接从变形梯度得到的。但是，有文献提到这些张量的物理意义并不直观，而在有限变形分析中最具有物理意义的是对数应变张量，这在非线性弹性力学中被称为“真实应变”。

Ludwik是被认为第一个在单轴意义下引入对数应变概念的人，然而，在非线性弹性领域的完整应用对数应变的工作仍归功于Hencky，他在1928年的一篇论文里，提出了连续介质力学框架的对数应变张量的概念，这个概念得到了广泛的认可，并将其称为Hencky应变。

对于物质的可压缩性分析中，使用主拉伸的自然对数来分析被证明是方便的，Hencky本人亲自展示了这种方法的有用性，基于的P. W. Bridgman对一系列不同的各向同性材料的广泛实验观察。Anand进一步证明了，针对小变形的Hookean形式应变能在将柯西应变替换为自然对数应变，也能很好地与大变形吻合。与该工作相关的非线性应变能的模型通常被称作各向同性超弹性的Hencky模型。

最近，Latorre and Montáns证明了对数剪切应变的几何意义，强调Hencky应变的特殊性质是，允许弹性体使用相同的体积-等体的能量分解。这在Xiao的工作得到证明，该文中提到大部分的有限应变测量都是耦合了球形和偏形部分，对数应变则可以适当地进行加法分解。最近，Neff给出了对数应变的物理特性和物理意义，再一次确认了Hencky应变是柯西无穷小应变的最自然推广。它们发现，线性Hookean模型和二次Hencky能量之间存在紧密的几何关系，在所有可能的有限应变张量中，只有对数应变张量满足共轴变形的叠加法则。

此外，Neff等人给出了二次Hencky应变能函数的几何解释，将其描述为变形梯度张量到特殊的二阶张量正交群的测地距离的平方。提供几何解释有助于科学家理解使用这种应变测量的动机，通常可以建立各分量的物理意义。在早期的工作中，Neff等人提出了Hencky能量的指数形式的解耦形式，并证明了模型的秩一凸性，进一步鼓励了自然对数应变的使用。

秩一凸性是指某个函数在其参数向量的每个方向上都是凸函数，具体来说，对于函数 ，如果对于任意的参数向量 和任意的标量 ，都有：

$$f(tx+(1-t)y)\le tf(x)+(1-t)f(y)$$
其中 和 是参数向量， 是一个标量。这个不等式表示函数在参数空间中的任意两点连线上的值都不大于这条线段的两端点对应的函数值的加权平均。如果一个函数满足这个性质，那么就称它是秩一凸的。秩一凸性在优化问题和凸分析中有重要的应用，因为它能够保证一些优化问题的收敛性和解的唯一性。

连续介质力学的唯象学方法

在连续介质力学中，唯象学方法是一种基于实验观察和经验规律的方法，而不涉及材料内部微观结构或基本物理原理的细节。这种方法的基本思想是通过观察和实验来建立材料的宏观行为和性质，而不需要了解其微观结构。在这种方法中，材料的行为通常由一些经验参数或材料参数来描述，这些参数通过实验测量或拟合来获得，而不需要深入研究材料的内部结构。尽管这种方法在描述材料的整体行为方面非常有效，但它可能无法提供对材料行为的深入理解，尤其是在考虑到材料微观结构对宏观行为的影响时。

通过指定特定的应变能函数，并一组适当的材料参数，这些参数可以控制连续体在任何给定的变形模式下的响应，这种方法叫做连续介质力学的唯象学方法。这是为了将其与统计方法区分开，统计方法致力于将力学响应与连续体分子结构联系起来，统计方法包括高斯理论或者大分子网络理论，而那些与橡胶相关的理论由Treloar发展得到。

最终，还是需要将唯象学方法和统计方法统一起来，Yeoh and Fleming指出，唯象学方法是可取的，直到某些基本的与分子概念相关的原理被发现，唯象学方法都只能被称为一种拟合曲线方法。唯象学方法被广泛采用，对于给定的橡胶弹性体或生物组织材料，都能找到大量的模型。形式不唯一，应变能函数需要满足的就只有凸性和不变性条件。

在实际操作中，一旦应变能函数的形式被确定，随后就导出本构定律，则可以校准材料参数，以此使得非线性模型可以最佳拟合给定的实验数据。所以，需要某种形式的回归分析使得可以确定最适合的材料参数，其中最常用的算法是Levenberg-Marquardt算法（见Mihai，Ogden，Twizell 的工作）。这个优化算法采用的是梯度下降法，所以只能得到非线性目标函数的局部最小解。因此，有评论指出，这些模型高度依赖解决方案所提供的初始种子。同时，这种拟合参数的优化唯象学方法并不能带来对纤维分布和微观结构响应的洞察，但是可以认为它是有效的，因为它符合所使用的实验数据的连续性特性。

提出一个非线性应变能函数并校准它以拟合数据，这是非常直接且可行的方法。但是，正如Yeoh所指出的那样，工程师们在能够将材料参数归于显著的物理意义上是具有挑战性的。具有物理意义的材料常数通常意味着它符合科学方法，可以在实验中反复测量。Truesdell and Noll建议将在唯象学连续介质力学框架下的变量当作统计分子作用的“平均值”。

最近，确定材料参数的计算流程应用了集成了机器学习的系统，Cilla等人利用三个不同的监督机器学习方法：支持向量机用于回归，Bagging决策树以及采用了人工神经网络的多感知机。该算法的使用分为两个阶段，一个是实施阶段，一个是验证阶段，用来衡量模型的好坏。文章承认机器学习在解决真实实验曲线存在的变异性时存在局限性，但认为计算开销上的显著降低可能使所提出的方法最终取代传统的基于梯度下降的优化方法。Liu等人采用机器学习技术分析主动脉壁，并发现一旦模型训练好，算法可以在一秒钟内估计所需的一组材料参数，这种确定材料参数的便利性对连续介质力学的唯象学方法是有益处。

2. 超弹性的不变量方法

应变能函数需要满足在所有的坐标变换下的不变性条件，即物质框架不变性原理。对于各向同性连续体，应变能可以写成对称的右柯西-格林变形张量的函数，使其在变换下保持客观性。

关于不变量理论与连续介质力学的关系最有用的工作来自Spencer，他详细介绍了具有不同内部对称性的二阶张量所需的完整基。文中提供的表格允许用户查阅给定系统的二阶张量的完整基和不变量。不变量，是向量和张量的函数性质，在正交变换保持不变。一个标量值各向同性张量函数被称为张量的不变量，其中迹函数被广泛使用。三维情况下，组成最小完整基的对称二阶张量的基本不变量是：

$$i_1=\mathrm{tr}(\mathrm{A}),{\mathrm{i}}_2=\mathrm{tr}({\mathrm{A}}^2),{\mathrm{i}}_3=\mathrm{tr}({\mathrm{A}}^3)$$
另外，三维情况下常用的主不变量如下：

$$I_1=\mathrm{tr}(\mathrm{A}),{\mathrm{I}}_2=\frac{1}{2}({\mathrm{tr}}^2(\mathrm{A})-\mathrm{tr}({\mathrm{A}}^2)),{\mathrm{I}}_3=\det (\mathrm{A})$$
主不变量构建二阶张量的特征多项式并以此得到Cayley-Hamilton理论。将 $i_1,i_2,i_3$称为基本不变量，以此区分$I_1,I_2,I_3$主不变量。

为了满足物质框架不变性原理和凸性条件，各向同性材料的应变能可以写成如下不变量形式：

$$\Psi =\Psi (I_1,I_2,I_3)$$
第三个主不变量是关于连续体在变形过程的体积变化。对于完全不可压缩的材料，其材料特性是在任何荷载作用下，都只有等体积变形。在这样的理想情况下，Attard和Hunt解释说可能存在一个不影响应变能的静水压力，因此应力不能通过常规方法直接确定。对于大多数的完全不压缩材料的研究，通常会对其第三主不变量施加一个约束，并将所需的静水压力 作为拉格朗日乘子包含其内。

完全不可压缩各向同性应变能密度如下表示：

$$\bar{\Psi }=\Psi (I_1,I_2)-pf(I_3-1)$$
然而，完全不可压缩材料是一种理想情况，真实情况是不可能出现，对于橡胶材料，在真实中会被当成一种近不可压缩材料。Kawabata等人，通过实验展示了异戊二烯橡胶的各向同性泊松比为0.499914，非常接近理论不可压缩极限的0.5。

人为地强制进行不可压缩状态可以极大地降低模型的数学复杂度以及固体所需的材料参数，然而，有人认为，最准确和最完整的材料模型还是需要包括可压缩性。

对于从各向同性到各向异性的发展，需要定义伪不变量。De Rosa等人指出，Rivlin类型的$I_1,I_2,I_3$ 主不变量的物理解释难以捉摸，使得文献研究开始考虑一种新的物理不变量方法来进行建模。Shariff和Criscione等人的文章中提供了替代的物理不变量作为例子，Criscione提出了一组针对横向各向同性的5个不变量，可以将应变的不同物理行为区分开。这允许应变能函数的不同部分可以直接由以下试验确定：一个不变量被扰动并测量，同时其他部分保持不变。然后，如果有的话，确定材料对该不变量应变行为的依赖程度。Shariff的上述引文扩展了“物理不变量”的概念，以涵盖各向异性响应。

类橡胶固体分析

在大应变下建立超弹性的应变能函数一开始仅适用于简单的各向同性情况，因为通过对橡胶固体行为分析表明，这些橡胶固体可以被承受很大的拉伸（最高可达700%），并且这种橡胶固体是被当作各向同性和近不可压缩材料的。在Treloar的工作中，广泛研究了橡胶的应力-应变行为，Treloar提供了非常优秀的实验数据，橡胶的本构模型通常以此作为基准。在他的工作中，设计了三种硫化橡胶的变形状态：单轴拉伸、双轴拉伸和纯剪切。研究了两种橡胶，第一种是8%硫橡胶，展示出最高直至400%的拉伸下仍具有可恢复弹性；第二种是基于乳胶的橡胶，当时经常用于工业应用。橡胶的特征是在实验中检测到的S形曲线，如下图所示：

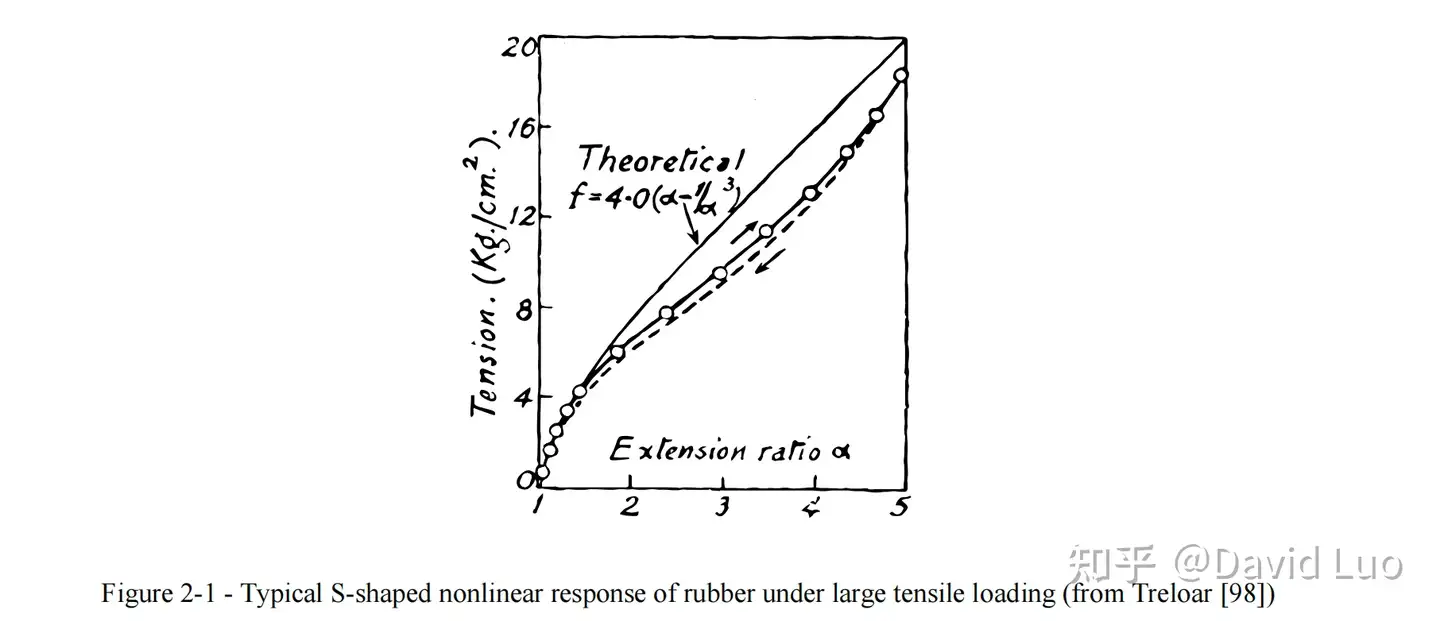
超弹性材料的各向同性应变能公式的大部分工作来自于Rivlin一系列关于《Large elastic deformations of isotropic materials》的开创性工作，在这里，Rivlin将应变能密度表示为右柯西-格林变形张量的三个主不变量的函数，Rivlin提出的本构模型系列可以写成如下：

$${\Psi }_{Rivlin}=\sum _{i,j=0}^N{C}_{ij}(I_1-3{)}^i(I_2-3{)}^j$$
其中， 是材料参数。可以发现，第三主不变量在这里看不到，这是由于事先假设橡胶弹性体是一个完全不可压缩材料。很多文献中的著名模型都是Rivlin模型系列的特殊例子，例如，当$j=0$ ，可以得到著名的neo-Hookean模型，用单个模型参数表征了非线性各向同性行为：

Ψ N H = C 10 ( I 1 − 3 ) \Psi_{NH} = C_{10}(I_1 - 3)