【多智能体系统】【H₂最优控制】H₂次优领航-跟随一致性控制的多智能体系统研究（Matlab代码、Simulink仿真实现）

本文链接：https://blog.csdn.net/Yan_she_He/article/details/145843580

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

⛳️赠与读者

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、Simulink仿真、文章

⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能解答你胸中升起的一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

**摘要**：本文研究了线性多智能体系统的分布式H₂次优领航-跟随一致性控制问题，采用动态输出反馈方法。考虑到一个自主领航者、多个跟随者以及相关的H₂代价函数，我们的目标是设计一个分布式协议，以确保在领航-跟随一致性达成的同时，相关的H₂代价小于预先给定的上界。为此，我们首先证明了H₂次优领航-跟随一致性控制问题可以等价地转化为一组独立系统的H₂次优控制问题。基于此，我们提出了一种计算分布式协议的设计方法。反馈增益的计算涉及两个黎卡提不等式，其维度与智能体的状态维度相匹配。通过一个仿真例子展示了所提协议的性能。
**关键词**：分布式控制、H₂最优控制、、次优控制、领航-跟随系统。

**1. 引言**
近二十年来，由于多智能体网络的潜在应用范围广泛，分布式控制的研究兴趣显著增加。研究了多种分布式控制场景，包括一致性（Olfati-Saber和Murray，2004）、围堵控制（Li等，2013）和编队控制（Oh等，2015）。作为多智能体系统的基本研究问题之一，一致性控制可以根据是否存在领导者分为无领导者一致性（Li等，2009）和领航-跟随一致性（Ni和Cheng，2010）。
本文研究领航-跟随一致性控制，即跟随者的状态应跟随领航者的状态。文献中已经研究了单积分器智能体系统的领航-跟随一致性控制，包括无向图（Jadbabaie等，2003）和有向图（Ren和Beard，2005），二阶跟随者智能体系统具有切换拓扑结构（Hong等，2008），一般线性系统在切换交互拓扑下（Ni和Cheng，2010）以及有向固定拓扑下（Li和Duan，2017）。
在实际中，智能体动态受到外部干扰的影响，可能导致多智能体系统性能恶化。在文献中，许多研究致力于解决领航-跟随一致性问题中的H∞性能保证。对于线性多智能体系统，Liu等（2015）通过考虑H∞性能区域，研究了基于静态状态反馈的领航-跟随一致性控制。与考虑性能区域不同，Zhang等（2017）研究了在切换连通拓扑下线性离散时间多智能体系统的领航-跟随一致性问题，采用静态状态协议实现规定的H∞性能衰减水平。与仅考虑系统理论概念不同，Pirani等（2019）提出了一种基于静态状态协议的图论方法，用于研究领航跟随一致性动态的H∞性能。然而，上述研究集中在H∞性能指标上，该指标衡量系统在最坏情况下的抗干扰能力。此外，上述研究考虑了静态状态反馈情况，而在实际中，通常只有智能体的输出测量值可用。
与此同时，也有研究关注无领导者多智能体系统的H₂性能，其中H₂性能指标表示系统在外部干扰下的误差能量。Li等（2011）研究了无向图下的无领导者一致性问题，考虑了H₂性能区域；Wang等（2014）研究了有向通信图下的H₂性能指标保证。与考虑性能区域不同，Jiao等（2018）基于静态状态反馈建立了次优分布式协议，Jiao等（2020）基于动态输出反馈建立了次优分布式协议，以最小化给定的H₂代价准则，同时实现多智能体系统的一致性。然而，在分布式H₂控制的背景下，对有领导者的领航-跟随一致性研究较少。
受上述研究的启发，本文研究基于动态输出反馈的领航-跟随多智能体系统的分布式H₂控制问题。具体而言，本文将Jiao等（2020）中无领导者系统的结果扩展到领航-跟随情况。为此，对于给定的领航-跟随系统，我们首先引入一个合适的性能输出，随后引入一个相关的H₂代价函数。目标是通过动态输出反馈设计分布式协议，使多智能体系统在最小化相关H₂代价函数的同时实现领航-跟随一致性。由于智能体之间的通信限制，这一问题是非凸的，迄今为止，文献中尚未给出封闭形式的解。因此，我们寻求一种仅涉及次优性的替代方案。
本文的结构如下：第2节介绍一些符号和图论基础知识。第3节阐述H₂次优领航-跟随一致性问题。第4节设计分布式H₂次优协议。第5节通过仿真例子展示所提协议的性能，第6节总结全文。

**6. 结论**
本文研究了基于动态输出反馈的分布式H₂次优领航-跟随一致性控制问题。对于一个包含N个智能体的多智能体系统，其中包含一个自主领航者和N−1个跟随者，以及一个具有期望上界的H₂代价函数，我们提出了一种计算分布式协议的设计方法，以实现H₂次优领航-跟随一致性。也就是说，跟随者的状态收敛到领航者状态，并且相关的H₂代价小于给定的上界。

详细文章见第4部分。

📚2 运行结果

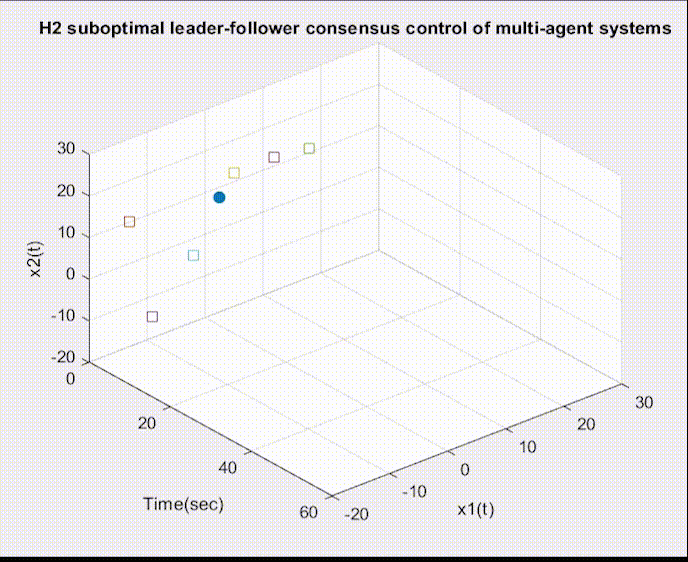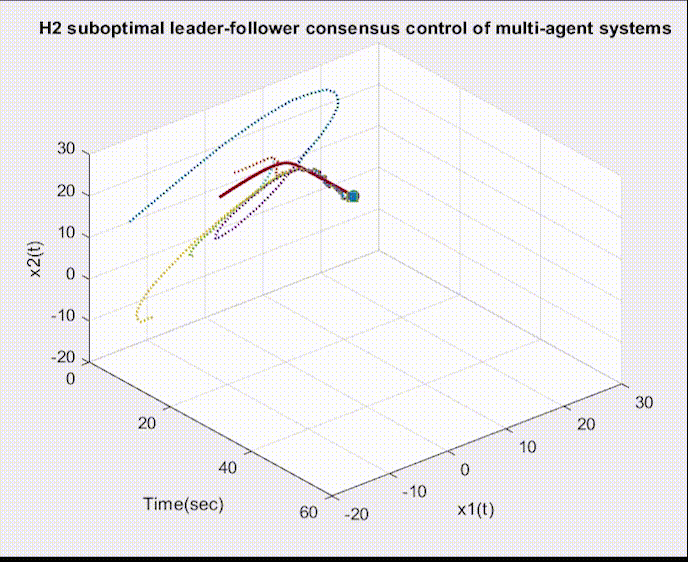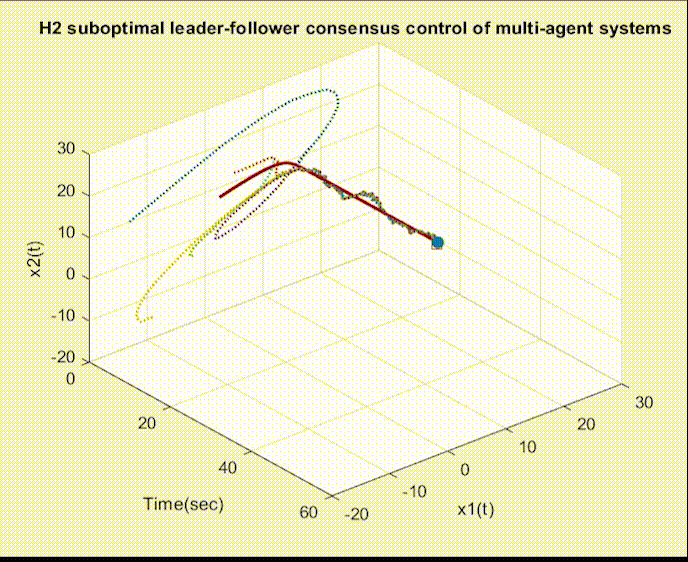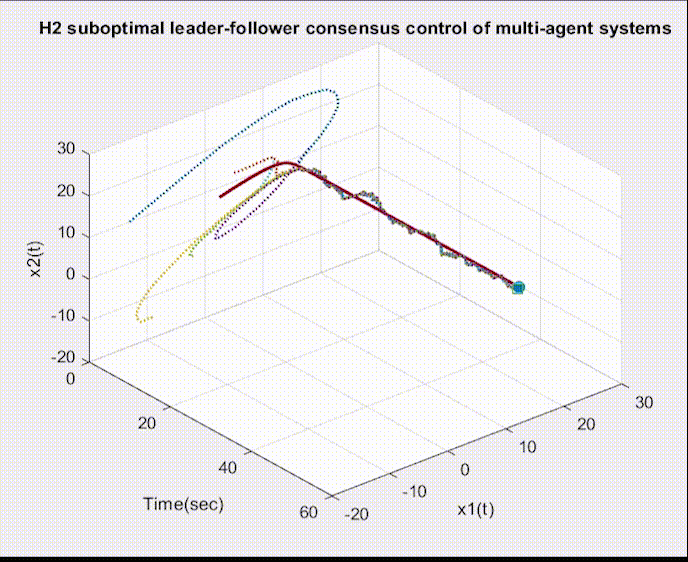
可视化部分代码：

figure4 = figure;
figure4.Position = [50 50 550 505];
ax(1)=subplot(2,1,1);
hold on
grid on
plot(T,x11(:,1)','LineWidth',2)
plot(T,x11(:,2)',':','LineWidth',1.5)
plot(T,x11(:,3)',':','LineWidth',1.5)
plot(T,x11(:,4)',':','LineWidth',1.5)
plot(T,x11(:,5)',':','LineWidth',1.5)
plot(T,x11(:,6)',':','LineWidth',1.5)
plot(T,x11(:,7)',':','LineWidth',1.5)
hold off
legend('x_{11}','x_{21}','x_{31}','x_{41}','x_{51}','x_{61}','x_{71}','Orientation','horizontal','Location','northoutside')
xlabel('Time(sec)')
ylim([-20 25])
ax(2)=subplot(2,1,2);
hold on 
grid on
plot(T,x12(:,1)','LineWidth',2)
plot(T,x12(:,2)',':','LineWidth',1.5)
plot(T,x12(:,3)',':','LineWidth',1.5)
plot(T,x12(:,4)',':','LineWidth',1.5)
plot(T,x12(:,5)',':','LineWidth',1.5)
plot(T,x12(:,6)',':','LineWidth',1.5)
plot(T,x12(:,7)',':','LineWidth',1.5)
legend('x_{12}','x_{22}','x_{32}','x_{42}','x_{52}','x_{62}','x_{72}','Orientation','horizontal','Location','northoutside')
xlabel('Time(sec)')
ylim([-20 30])
MagInset(figure4, ax(1), [30 60 10 15], [15 45 -13 2], {'NE','SE';'SW','NW'});
MagInset(figure4, ax(2), [30 60 10 15], [15 45 -13 2], {'NE','SE';'SW','NW'});
hold off

figure5 = figure;
figure5.Position = [50 50 550 520];
ax(1)=subplot(2,1,1);
hold on
grid on
plot(T,ep1(:,1)','LineWidth',1)
plot(T,ep1(:,2)','LineWidth',1)
plot(T,ep1(:,3)','LineWidth',1)
plot(T,ep1(:,4)','LineWidth',1)
plot(T,ep1(:,5)','LineWidth',1)
plot(T,ep1(:,6)','LineWidth',1)
hold off
legend('\epsilon_{11}','\epsilon_{21}','\epsilon_{31}','\epsilon_{41}','\epsilon_{51}','\epsilon_{61}','Orientation','horizontal','Location','northoutside')
xlabel('Time(sec)')
ylim([-55 35])
ax(2)=subplot(2,1,2);
hold on 
grid on
plot(T,ep2(:,1)','LineWidth',1)
plot(T,ep2(:,2)','LineWidth',1)
plot(T,ep2(:,3)','LineWidth',1)
plot(T,ep2(:,4)','LineWidth',1)
plot(T,ep2(:,5)','LineWidth',1)
plot(T,ep2(:,6)','LineWidth',1)
legend('\epsilon_{12}','\epsilon_{22}','\epsilon_{32}','\epsilon_{42}','\epsilon_{52}','\epsilon_{62}','Orientation','horizontal','Location','northoutside')
xlabel('Time(sec)')
ylim([-25 25])
MagInset(figure5, ax(1), [30 60 -6 6], [15 45 12 32], {'NE','NE';'SW','SW'});
MagInset(figure5, ax(2), [30 60 -4 4], [15 45 12 22], {'NE','NE';'SW','SW'});
hold off