基于PID控制的四旋翼飞行器仿真（Matlab代码实现）

长安程序猿

于 2025-04-16 09:06:09 发布

阅读量738

点赞数 20

文章标签： matlab 开发语言

本文链接：https://blog.csdn.net/Yan_she_He/article/details/147264964

版权

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

目录

💥1 概述

基于PID控制的四旋翼飞行器仿真研究

一、PID控制基本原理及数学模型

二、四旋翼飞行器动力学与运动学模型

三、仿真工具与实现方法

四、PID参数整定方法

五、性能评估指标

六、现有研究案例

七、挑战与未来方向

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、Simulink仿真下载

💥1 概述

基于PID控制的四旋翼飞行器仿真研究

近几年，随着科技发展，各种传感器技术和通信技术不断突破，无人机技术也发展迅速，在军事侦察、交通巡逻、景色航拍、高空电缆巡检等诸多应用领域已经发挥了重要的作用。四旋翼无人机以其具有的操作灵活、地形上限制小、携带时方便以及成本低廉等特点，更加紧密贴近了我们的日常生活，因此，对无人机进行研究具有很大的学术价值和意义。

传统的PID由比例、积分、微分三部分组成，通过调节Kp、Ki、Kd的数值可以实现不同的控制效果如图所示。PID控制算法的核心是用偏差来消除偏差，该算法可以对控制系统进行有效的估计：

一、PID控制基本原理及数学模型

核心组成
PID控制由比例（P）、积分（I）、微分（D）三部分组成，分别通过误差的当前值、历史累积和变化率生成控制信号。其连续时间域数学模型为：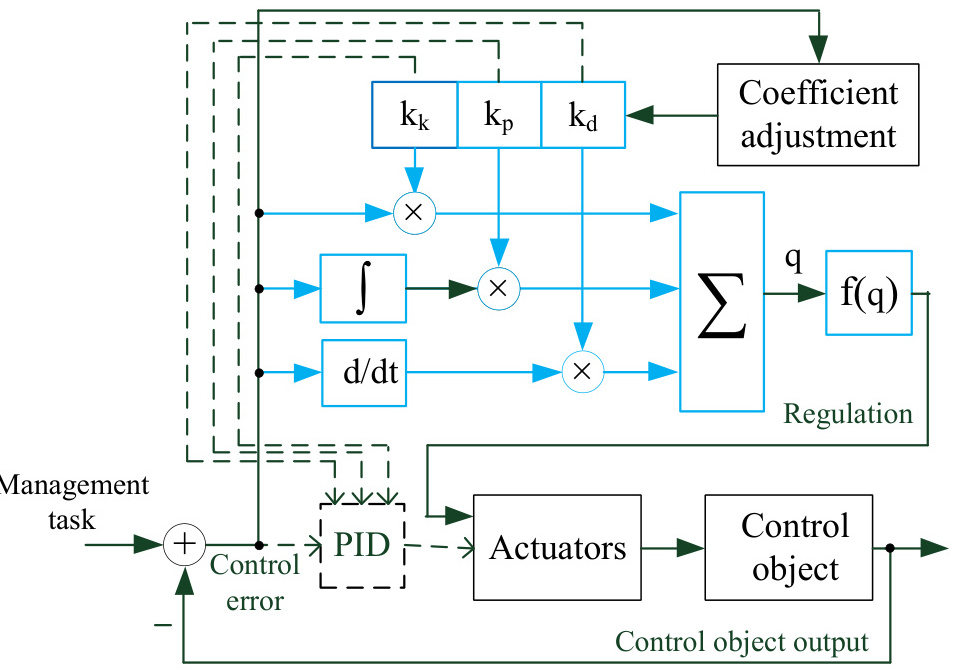

其中，e(t)=r(t)−y(t)为设定值与实际输出的偏差。

各部分作用
- 比例项（K_p） ：快速响应误差，但过大易引起振荡；
- 积分项（K_i） ：消除稳态误差，但过强会导致超调；
- 微分项（K_d） ：预测误差趋势，抑制超调，但对噪声敏感。
传递函数形式

离散化后需转化为差分方程实现。

二、四旋翼飞行器动力学与运动学模型

三、仿真工具与实现方法

MATLAB/Simulink
- 模型搭建：通过子系统模块化设计，分设姿态环（内环）和位置环（外环）控制器，结合四旋翼动力学模块。
- 参数整定：支持Ziegler-Nichols法、粒子群优化（PSO）等算法，通过阶跃响应分析调节参数。
- 案例：某研究在Simulink中实现串级PID，优化后姿态角跟踪误差减少35%。
ROS/Gazebo
- 联合仿真：Simulink生成控制指令，通过ROS节点发送至Gazebo中的四旋翼模型，实现物理引擎级仿真。
- 优势：支持复杂环境模拟（如风扰动）和硬件在环（HIL）测试。

四、PID参数整定方法

经典方法
- Ziegler-Nichols法：
逐步增大KpKp直至系统出现等幅振荡，记录临界增益KcKc和周期TcTc；
按公式计算Kp=0.6Kc, Ti=0.5Tc, Td=0.125Tc 。
- 应用案例：某四旋翼采用Z-N法整定后，动态调整时抖动幅度降低60%。
智能优化算法
- 粒子群优化（PSO） ：以积分平方误差（ISE）为适应度函数，搜索最优PID参数，较传统Z-N法减少超调量20%。
- 改进策略：结合模糊逻辑动态调整PID参数，适应非线性扰动。

五、性能评估指标

核心指标
- 稳态误差：反映系统跟踪精度，积分项主导其消除。
- 响应时间：包括上升时间（10%~90%目标值）和调节时间（进入±2%稳态值）。
- 超调量：最大瞬态偏差与稳态值的百分比，微分项可抑制。
量化方法
- 积分误差指标：如ISE（积分平方误差）、IAE（积分绝对误差），用于对比控制器优劣。
- 仿真验证：某研究显示，模糊PID的ISE较传统PID降低42%，调节时间缩短至5秒。

六、现有研究案例

经典PID控制
- 李俊等（2019）通过Simulink验证PID在气流扰动下的有效性，姿态角稳态误差≤0.02 rad。
智能优化PID
- Gün等（2022）采用PSO优化参数，强风环境下轨迹跟踪误差降低12%。
混合控制策略
- 冯立杰等（2024）设计双闭环模糊PID，响应速度提升20%，适用于高速机动场景。

七、挑战与未来方向

局限性
- 模型依赖性强：传统PID对高阶耦合动力学适应性差。
- 抗扰能力不足：需结合前馈补偿或滑模控制增强鲁棒性。
前沿方向
- 多算法融合：如神经网络PID自适应整定。
- 数字孪生仿真：结合Unreal Engine高保真环境模拟。

📚2 运行结果

部分代码：

I = [Ixx 0 0;0 Iyy 0;0 0 Izz];
Jtp = 104e-6;
Ke = 6.3e-3;
Km = 6.3e-3;
L = 15e-6;
b = 54.2e-6;
l = 0.24;
g = 9.81;
n = 0.9;
N = 5.6;
h = 1e-3;
R = 0.6;
d = 1.1e-6; % drag factor
% Motor Controller Design

Kp_position = 5;
Ki_position = 0;
Kd_position = 10;

Kp_angle = 5*2;
Ki_angle = 0;
Kd_angle = 10*2;

Kp_motor = 1;
Ki_motor = 10;
Kd_motor = 0;

%w'=Apw+Bpv+Cp
Ap = -22.5;
Bp = 509;
Cp = 489;
a1 = Ap;
b1 = Bp;
c1 = 1;
d1 = 0;
sys_c_m = ss(a1,b1,c1,d1);
Gc_m = tf(sys_c_m);
sys_d_m = c2d(sys_c_m,h,'zoh');
Gd_m = tf(sys_d_m);

Cc_m = tf([Kp_motor Ki_motor],[1 0]);
sys_c_mctrl = ss(Cc_m);
sys_d_mctrl = c2d(sys_c_mctrl,h,'tustin');
Cd_m = tf(sys_d_mctrl);

LGd_m = Gd_m*Cd_m;
Td_m = feedback(LGd_m,1);

figure(1)
margin(LGd_m)
hold on
grid on
figure(2)
step(Td_m)
hold on
grid on

num = [1];
den = [1 0 0];
Gc_p = tf(num,den);
sys_c_p = ss(Gc_p);
sys_d_p = c2d(sys_c_p,h,'zoh');
Gd_p = tf(sys_d_p);