【六种超级棒的改进差分优化算法】SaDE、JADE，SHADE，LSHADE、LSHADE_SPACMA、LSHADE_EpSin差分优化算法（Matlab代码实现）

    💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

 ⛳️赠与读者

💥1 概述

1. SaDE（Self-adaptive Differential Evolution）

2. JADE（Adaptive Differential Evolution with Optional External Archive）

3. SHADE（Success-history based Adaptive Differential Evolution）

4. LSHADE（Linear-SHADE）

5. LSHADE_SPACMA

6. LSHADE_EpSin

总结

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、文章下载

---

 ⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能解答你胸中升起的一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

     或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

【六种超级棒的改进差分优化算法】SaDE、JADE，SHADE，LSHADE、LSHADE_SPACMA、LSHADE_EpSin差分优化算法研究

SaDE（Self-adaptive Differential Evolution）

SaDE算法是一种改进的差分进化（DE）算法，其核心特点在于能够自适应地调整算法的控制参数，以适应不同阶段的优化需求。这种算法不需要预先指定学习策略和两个控制参数F（缩放因子）与CR（交叉概率），而是在进化过程中根据学习经验逐渐自我适应这些参数。

JADE（Adaptive Differential Evolution with Optional External Archive）

JADE算法是一种改进的差分进化（DE）算法。

JADE算法能够自动调整控制参数，如缩放因子（F）和交叉概率（CR），以适应优化问题的特性，从而提高算法的鲁棒性。

JADE算法引入了“DE/current-to-pbest”变异策略，这是对经典“DE/current-to-best”策略的扩展。在“DE/current-to-pbest”中，不仅考虑当前个体和最好个体之间的差异，还可能包含历史最优个体的信息，这样可以增加种群的多样性，避免过早收敛，同时也能改善算法的收敛性能。

JADE算法引入了可选的外部归档机制，用于存储历史最优解。这些历史数据可以提供优化过程中的进步方向信息，帮助算法跳出局部最优，提高全局搜索能力。

SHADE（Success-history based Adaptive Differential Evolution）

SHADE算法是一种基于差分进化（DE）算法的自适应优化算法，由Tanabe和Fukunaga于2013年提出。SHADE算法在JADE的基础上进行了改进，主要通过引入成功历史记忆机制来优化控制参数，从而提高算法的收敛性和搜索能力。

LSHADE（Linear-SHADE）

LSHADE（Linear-SHADE）优化算法是一种基于差分进化（DE）算法的优化算法，其核心特点在于引入了线性种群规模缩减（Linear Population Size Reduction, LPSR）机制。

LSHADE_SPACMA

LSHADE_SPACMA优化算法是一种结合了LSHADE（Large Population Size Reduction SHADE）和CMA-ES（Covariance Matrix Adaptation Evolution Strategy）的混合优化算法

LSHADE_EpSin

• LSHADE_EpSin算法通过引入一种新的正弦参数自适应框架来改善L-SHADE算法的性能。这种框架能够自动调整差分进化算法中的缩放因子（F）的值。

• 该算法采用了两种正弦公式的混合：非自适应正弦递减调整和基于历史的自适应正弦递增调整。这种正弦集成方法的目标是在已找到的最佳解的利用和未访问区域的探索之间找到有效的平衡。

• 在后期代数中，LSHADE_EpSin还使用了基于高斯步行的局部搜索方法，以增强其利用能力。

差分进化（Differential Evolution, DE）是一种基于群体差异的启发式优化算法，广泛应用于各种连续优化问题。以下是六种改进的差分进化算法（SaDE、JADE、SHADE、LSHADE、LSHADE_SPACMA、LSHADE_EpSin）的详细研究文档。

1. SaDE（Self-adaptive Differential Evolution）

核心特点：

• 自适应参数调整：SaDE算法在进化过程中自适应地调整缩放因子（F）和交叉概率（CR），无需预先指定学习策略。
• 学习经验：算法根据个体的历史学习经验逐渐调整控制参数，以适应不同阶段的优化需求。

优势：

• 提高了算法的鲁棒性和适应性。
• 减少了手动调整参数的复杂性和时间成本。

2. JADE（Adaptive Differential Evolution with Optional External Archive）

核心特点：

• 自动参数调整：自动调整F和CR以适应优化问题特性。
• DE/current-to-pbest变异策略：扩展了经典“DE/current-to-best”策略，增加种群多样性，避免过早收敛。
• 外部归档机制：存储历史最优解，提供优化方向信息，帮助跳出局部最优。

优势：

• 提高了算法的收敛速度和全局搜索能力。
• 通过外部归档机制增强了算法的历史记忆能力。

3. SHADE（Success-history based Adaptive Differential Evolution）

核心特点：

• 成功历史记忆机制：引入成功历史记忆来优化控制参数，提高收敛性和搜索能力。
• 基于JADE的改进：在JADE算法基础上进行改进，增强了算法的自适应性。

优势：

• 提高了算法的成功率和稳定性。
• 通过记忆机制加速了收敛过程。

4. LSHADE（Linear-SHADE）

核心特点：

• 线性种群规模缩减（LPSR）机制：在进化过程中线性减少种群规模，以提高算法的计算效率。
• 基于SHADE的改进：在SHADE算法基础上引入LPSR机制。

优势：

• 减少了计算资源消耗。
• 在保持算法性能的同时提高了收敛速度。

5. LSHADE_SPACMA

核心特点：

• 结合LSHADE和CMA-ES：融合了LSHADE算法的大种群规模缩减机制和CMA-ES（协方差矩阵自适应进化策略）的高效搜索能力。
• 混合优化策略：结合了两种算法的优点，提高了算法的全局搜索和局部搜索能力。

优势：

• 增强了算法的全局和局部搜索平衡性。
• 提高了算法在复杂优化问题上的性能。

6. LSHADE_EpSin

核心特点：

• 正弦参数自适应框架：引入新的正弦参数自适应框架来调整F的值，平衡利用和探索。
• 混合正弦公式：采用非自适应正弦递减调整和基于历史的自适应正弦递增调整。
• 高斯步行局部搜索：在后期代数中使用高斯步行增强利用能力。

优势：

• 提高了算法在探索和利用之间的平衡性。
• 通过高斯步行增强了算法的局部搜索能力。

总结

这六种改进的差分进化算法各有优势，适用于不同的优化问题和场景。SaDE、JADE和SHADE算法通过自适应参数调整提高了算法的鲁棒性和收敛性；LSHADE算法通过线性种群规模缩减提高了计算效率；LSHADE_SPACMA算法结合了LSHADE和CMA-ES的优点，增强了全局和局部搜索能力；LSHADE_EpSin算法通过正弦参数自适应框架和高斯步行局部搜索提高了算法在探索和利用之间的平衡性。在实际应用中，可以根据具体问题和需求选择合适的算法进行优化。

📚2 运行结果

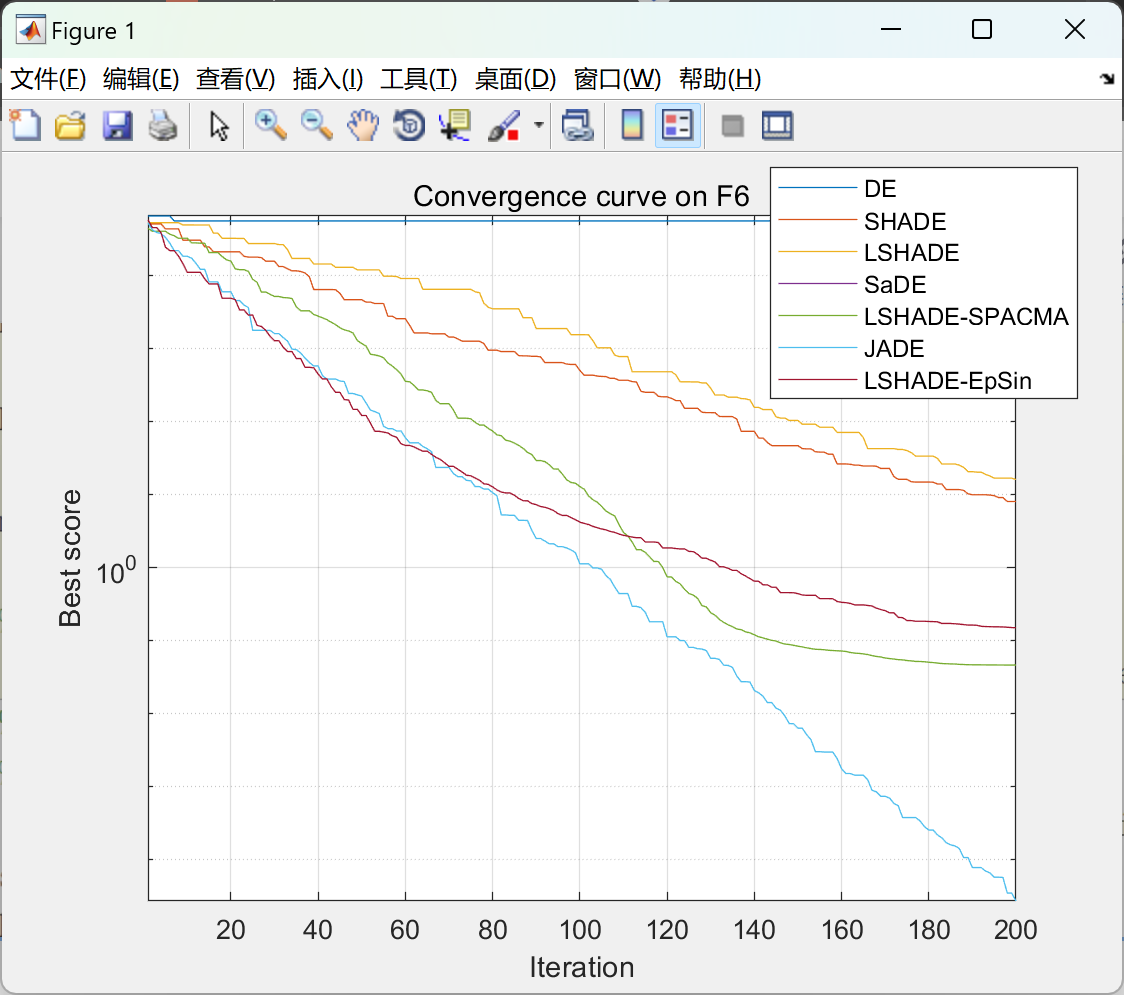
部分代码：

top=round(p*pop); %每代中最优的top个
A=[];%初始归档种群为空集
tt=1;%记录归档种群A中的个体个数

% 初始 CR F
uCR=0.5;%初始化交叉概率
uF=0.5;%初始化缩放因子

% 种群初始化
P = repmat(lu(1, :), pop, 1) + rand(pop, dim) .* (repmat(lu(2, :) - lu(1, :), pop, 1));
fitnessP=zeros(1,pop);
for i=1:pop
    fitnessP(i)=fobj(P(i,:));
end

% 主迭代
t=0;%设置迭代器（当前迭代代数）
while t < Tmax

    Scr=[];%初始成功参加变异的个体的交叉概率为空集
    Sf=[];%初始成功参加变异的个体的缩放因子为空集
    n1=1;%记录Scr中的元素个数
    n2=1;%记录Sf中的元素个数

    % 更新适应度和CR F
    for i=1:pop
        fitnessP(i)=fobj(P(i,:));
        % 更新
        CR(i)=0.5;
        F(i)=0.5;
        while (CR(i)>1||CR(i)<0)
            CR(i)=normrnd(uCR,0.1);
        end
        if (F(i)>1)
            F(i)=1;
        end
        while (F(i)<=0)
            F(i)=cauchyrnd(uF,0.1);
        end
    end

    % 获得种群前p个个体，方便后面随机选择
    [fitnessBestP,indexBestP]=min(fitnessP);
    bestP=P(indexBestP,:);
    [~,indexSortP]=sort(fitnessP);
    for i=1:top
        bestTopP(i,:)=P(indexSortP(i),:);
    end

    % 变异操作
    for i=1:pop
        %从top个个体中随机选出一个作为Xpbest
        k0=randperm(top,1);
        Xpbest=bestTopP(k0,:);

        %从当前种群P中随机选出P1
        k1=randi(pop);
        P1=P(k1,:);
        while (k1==i||k1==k0)
            k1=randi(pop);
            P1=P(k1,:);
        end

        %从P∪A中随机选出P2
        PandA=[P;A];
......

%% 
% DE
[best_f,best_x,cg] = DE(population_size,max_iter, lb, ub, dim,fitness_function);
semilogy(cg)
hold on
% SHADE 
[best_f1,best_x1,cg1] = SHADE(population_size,max_iter, lb, ub, dim,fitness_function);
semilogy(cg1)
hold on
% LSHADE
[best_f2,best_x2,cg2] = LSHADE(population_size,max_iter, lb, ub, dim,fitness_function);
semilogy(cg2)
hold on
% SaDE
[best_f3,best_x3,cg3] = SaDE(population_size,max_iter, lb, ub, dim,fitness_function);
semilogy(cg3)
hold on
% LSHADE_SPACMA
[best_f4,best_x4,cg4] = LSHADE_SPACMA(population_size,max_iter, lb, ub, dim,fitness_function);
semilogy(cg3)
hold on
% JADE
[best_f5,best_x5,cg5] = JADE(population_size,max_iter, lb, ub, dim,fitness_function);
semilogy(cg5)
hold on
% LSHADE_EpSin
[best_f6,best_x6,cg6] = LSHADE_EpSin(population_size,max_iter, lb, ub, dim,fitness_function);
semilogy(cg6)
hold on
%% Display results
disp('Optimization complete.');
title(['Convergence curve on ' Function_name])
xlabel('Iteration');
ylabel(['Best score']);
legend('DE','SHADE','LSHADE','SaDE','LSHADE-SPACMA','JADE','LSHADE-EpSin')
axis tight
grid on
box on 

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。(文章内容仅供参考，具体效果以运行结果为准)

[1] A. K. Qin and P. N. Suganthan, "Self-adaptive differential evolution algorithm for numerical optimization," 2005 IEEE Congress on Evolutionary Computation, Edinburgh, UK, 2005, pp. 1785-1791 Vol. 2. 

[2] J. Zhang and A. C. Sanderson, "JADE: Adaptive Differential Evolution With Optional External Archive," in IEEE Transactions on Evolutionary Computation, vol. 13, no. 5, pp. 945-958, Oct. 2009.

[3] R. Tanabe and A. Fukunaga, "Success-history based parameter adaptation for Differential Evolution," 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 2013, pp. 71-78. 

[4] R. Tanabe and A. S. Fukunaga, "Improving the search performance of SHADE using linear population size reduction," 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 2014, pp. 1658-1665. 

[5] A. W. Mohamed, A. A. Hadi, A. M. Fattouh and K. M. Jambi, "LSHADE with semi-parameter adaptation hybrid with CMA-ES for solving CEC 2017 benchmark problems," 2017 IEEE Congress on Evolutionary Computation (CEC), Donostia, Spain, 2017, pp. 145-152. 

[6] N. H. Awad, M. Z. Ali, P. N. Suganthan and R. G. Reynolds, "An ensemble sinusoidal parameter adaptation incorporated with L-SHADE for solving CEC2014 benchmark problems," 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 2016, pp. 2958-2965, doi: 10.1109/CEC.2016.7744163.

🌈4 Matlab代码、文章下载

资料获取，更多粉丝福利，MATLAB|Simulink|Python资源获取