【Python】Section 5: 分类和逻辑回归 Classification and Logistic Regression from HarvardX

1. Classification and kNN

1.1 Classification

Classification is the problem of predicting a discrete label- for example, predicting whether the patient has the value "Yes" or "No" in the AHD (heart disease) column.

Age	RestBP	Thal	...	AND
63	145	Fixed	...	No
67	108	Normal	...	Yes
...	...	...	...	...
41	130	Reversable	...	No

 

A key example of classification is medical diagnosis. We can use one (or more) of the features in the data to try and predict whether AHD will be true or false. This can help doctors find patients most at risk of developing heart disease. Similar to regression, we can use any number of features as the inputs to our model.

Our model's response/target variables in a classification problem are categorical. Some examples of categorical targets are:

• The binary target of whether a patient has heart disease
• The 3-dimensional target of a self-driving car scanning a traffic light to determine if the light is green, yellow, or red.
• The 5-dimensional target of a weather-prediction model that is trying to determine if tomorrow's description will be Rain, Snow, Cloudy, Sunny, or Partly Cloudy
• Grouping customers into similar "types"

In the following section we will focus on two algorithms for classification:

• k-Nearest Neighbors classification (similar to the kNN algorithm for regression)
• Logistic regression

1.2 kNN for Regression

The k-Nearest Neighbors (kNN) algorithm works for both regression and classification. In both cases, a kNN model makes predictions on new data points using the k most similar points from our training dataset.

kNN for Regression

For each value of k, our output value is the average of the k nearest neighbors' outputs:

kNN for Classification

We classify a data point  based on the labels of its neighbors

\[P\left( Y=j | X=x_0 \right) = \frac{1}{k}\sum_{i\in N_0}\ \ I\left(y_i=j\right)\]

 is defined as the set of the  nearest neighbors to .

 is the indicator function, equal to 1 when neighbor  has the label  and equal to 0 otherwise.

This formula builds a probability distribution for the class as the relative frequency of the classes in the set of neighbors .

For example, if there are  neighbors of , and 10 of the neighbors have label , then the probability that  has that same label  is given by

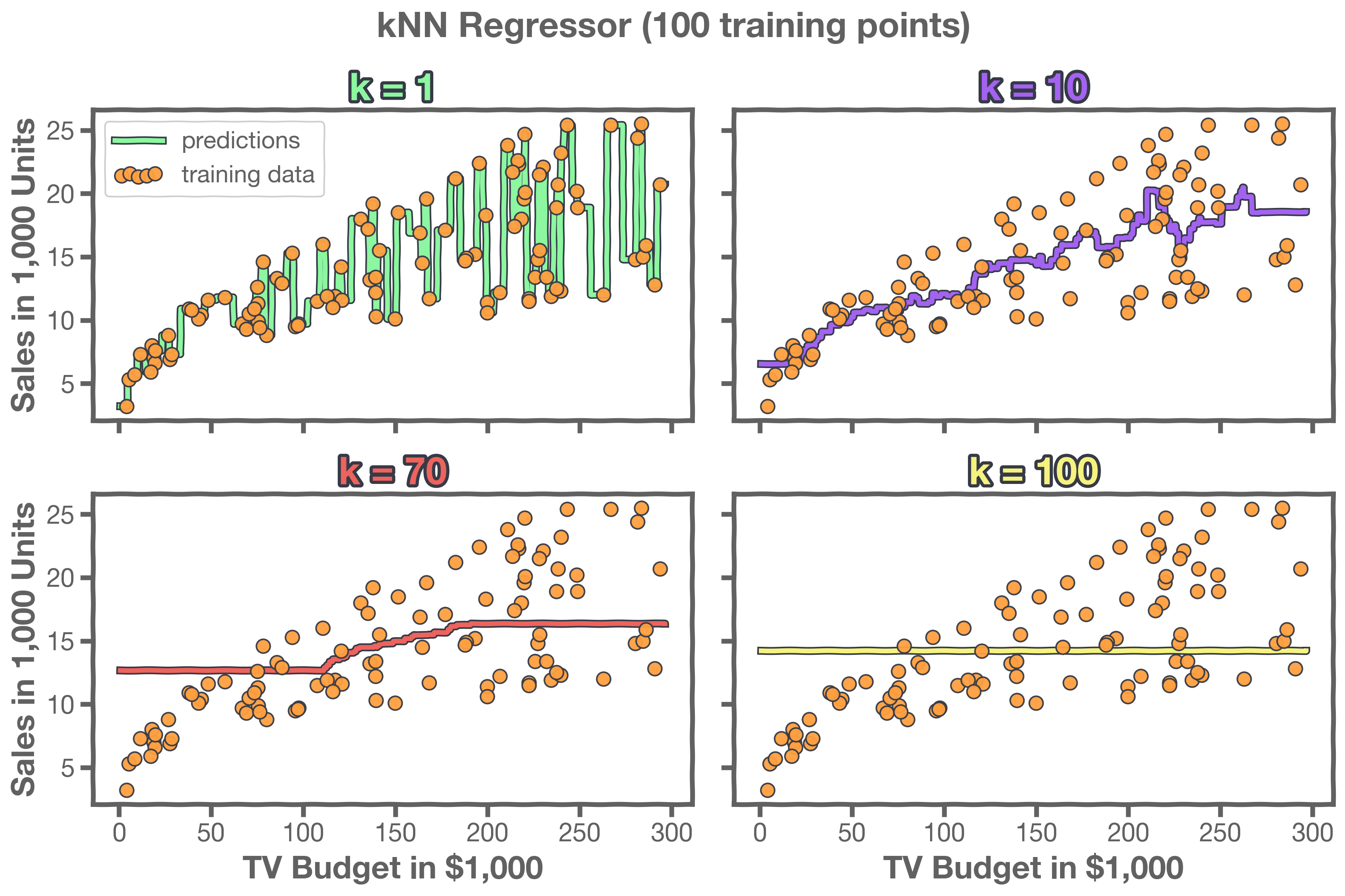
Changing the number of neighbors k: how smooth should our model be?

Notice that the behavior of kNN for classification is similar to kNN for regression: as we increase k, we tend to see a smoother pattern in our model. Here's an example:

Here's another set of examples:

How do we identify similar data points when the data has many features?

Here we walk through an example of standardizing a dataset so that we can get a better "distance" measurement between multi-dimensional data that includes a mix of quantitative and categorical features. In Python, you can use sklearn.preprocessing.StandardScaler to do this.

Suppose you are working for a movie ticket purchasing website. Users create an account for your website through an existing social media app. Your job is to build a model that can predict a user's favorite movie genre. You have access to some survey data your company recently collected:

feature	data type
year born	integer
new user	boolean, True for new users, False otherwise
# social media friends	integer
favorite genre	categorical from 4 options: Comedy, Action, Romance, and SciF

Using this data, you can build a k-nearest neighbors algorithm to try and predict, for other users not included in the dataset, what their favorite genre is.

Original unscaled data

Year Born	New /Existing User	# Friends	Favorite Genre
1998	0	312	Action
1992	1	65	SciFi
2001	1	1923	Comedy
1987	0	203	Romance
1974	1	767	Romance
2000	0	54	Action

Consider a user born in 1990, who is an existing user with 1000 friends. We represent this new user as

User = [1990, 0, 1000]

and compute a Euclidean distance measurement with our existing users in our dataset. For example, the distance between User and our first row of data is given by

Year Born	New/Existing User	# Friends	Favorite Genre	Euclidean Distance to User
1998	0	312	Action	688.05
1992	1	65	SciFi	935.00
2001	1	1923	Comedy	923.07
1987	0	203	Romance	797.00
1974	1	767	Romance	233.55
2000	0	54	Action	946.05

Now we can predict User's favorite genre using k=3 nearest neighbors. The nearest neighbors are rows 1, 4, and 5. We assign a 2/3 probability that User's favorite genre is Romance based on the two neighbors who prefer Romance, and a 1/3 probability the favorite genre is Action based on the one neighbor who prefers Action- and therefore we would predict the label Romance.

But what is possibly going wrong here? Our distance measurement is flawed because most of the distance is coming from the difference in the # of friends, therefore under-reacting to the difference in year born. We have not given any reason why we should want out distance measurement to depend more on one feature than another. In the absence of such an explicit reason we should have the distance measure treat all features equally.

Scaled data using standard scaler

One way to get a balanced distance between data, regardless of the specific features, is to "standardize".

Standardization

Standardizing means applying this formula:

to each feature  for all the rows in the dataset.

Scaled User: [-0.213, -1.0, 0.679]

Scaled Year Born	Scaled New/Existing User	Scaled # Friends	Favorite Genre	Euclidean Distance to Scaled User
0.638	-1.0	-0.368	Action	1.349
0.0	1.0	-0.744	SciFi	2.464
0.958	1.0	2.083	Comedy	2.710
-0.532	-1.0	-0.534	Romance	1.254
-1.915	1.0	0.324	Romance	2.650
0.851	-1.0	-0.761	Action	1.790

Now we can predict User's favorite genre using k=3 nearest neighbors. This time-nearest neighbors are rows 1, 4, and 6. We assign a 2/3 probability that User's favorite genre is Action based on the two neighbors who prefer Action, and a 1/3 probability that the favorite genre is Romance based on the one neighbor who prefers Romance- and therefore we would predict the label Action.

Is this a better distance function, and is it better that this time our model labeled Action instead of Romance? Well, without the actual labels for the data we cannot know for certain. But this time, with scaled data, our model is recognizing the similarities/differences in age at the same level of importance as the similarities/differences in the # of friends. So we can at least have more confidence that our model will be learning more directly from patterns in the data.

2. Logistic Regression

To learn our logistic model through optimization:

1. We compute the log-likelihood function, which is the loss function of our model.
2. We compute the derivative of the log-likelihood function for gradient descent optimization.

2.1 Computing the log-likelihood function

We compute how well our logistic model fits the data by comparing its output probabilities with the labels for each data point, using a likelihood function.

The likelihood function for our  (between 0 and 1) and the real  (either 0 or 1) is given by:

We use this formula because when the label  is 1, the likelihood is  , and when the label  is 0, the likelihood is .

To get our total likelihood, we multiply the likelihoods of all our data points (using the capital greek letter  to represent a product for all i)

However, an easier function to optimize is the log-likelihood.

Review from previous section

The log function is "convex", so if we find an optimum for the log-likelihood, it is equivalently an optimum for the total likelihood. And since the log-likelihood is an expression of a sum instead of a product, it is computationally easier to optimize. To turn the procedure into a minimization instead of a maximization, we seek to minimize negative log-likelihood instead of maximize log-likelihood.

Our log-likelihood function is

We simplified the equation by converting the log of a product into a sum of logs

We simplify the equation again by converting a log of products into a sum of logs

Finally we move the exponents within the log term to be products outside the log term

Our loss function will be the average log-likelihood of our data points instead of the total log-likelihood, so that we can equally compare the log-likelihoods when the number of data points changes.

Here is a NumPy implementation of this loss function which is vectorized, meaning you can use it for any number of beta parameters in a vector called beta. Our work so far has assumed that  for a one-dimensional dataset,  . But the code below would also work for  for a ten-dimensional .

sigmoid = lambda x : 1 / (1 + np.exp(-x))
def loss(X, y, beta, N):
    # X: inputs, y : labels, beta : model parameters, N : # datapoints
    p_hat = sigmoid(np.dot(X, theta))
    return -(1/N)*sum(y*np.log(p_hat) + (1 - y)*np.log(1 - p_hat))

2.2 Computing the derivative of the log-likelihood function for gradient descent optimization

To optimize our logistic regression model, we want to find beta parameters to minimize the above equation for negative log-likelihood. This corresponds to finding a model whose output probabilities most closely match the data labels.

To compute our derivative, we first calculate the derivative of loss with respect to the probabilities , then calculate the derivative of the probabilities with respect to our beta parameters. Using the chain rule, we will derive a simple formula for the derivative of our loss.

Calculating the derivative of the loss with respect to our model probabilities

Since the derivative of log(x) is 1/x, the derivative of our loss function with respect to the probabilities  is

The derivative of  with respect to our Beta parameters (using the chain rule) is

To simplify this equation, we can re-write it directly in terms of the probabilities :

Calculating the derivative of the loss with respect to our model parameters

Due to the chain rule, the derivative of our loss is

This final sum of products can be re-written as a dot product in the following way, making our Python implementation simpler:

Here is a NumPy implementation of the derivative of our loss function.

def d_loss(X, y, theta, N):
    # X: inputs, y : labels, beta : model parameters, N : # datapoints
    p_hat = sigmoid(np.dot(X, beta))
    return np.dot(X.T,-(1/N)*(y*(1 - p_hat) - (1 - y)*p_hat))

To use gradient descent, we start with an initial guess for our Beta parameters, and then update them by small steps in the direction that results in fitting the data better. That is, in the direction of lowest negative log-likelihood. After each step we can compute the loss to track the progress of the optimization.

step_size = .5
n_iter = 500
beta = np.zeros(2) # initial guess for Beta_0 and Beta_1
losses = []
for _ in range(n_iter):
    beta = beta - step_size * d_loss(beta)
    losses.append(loss(beta))

Turning probabilities into discrete classifications

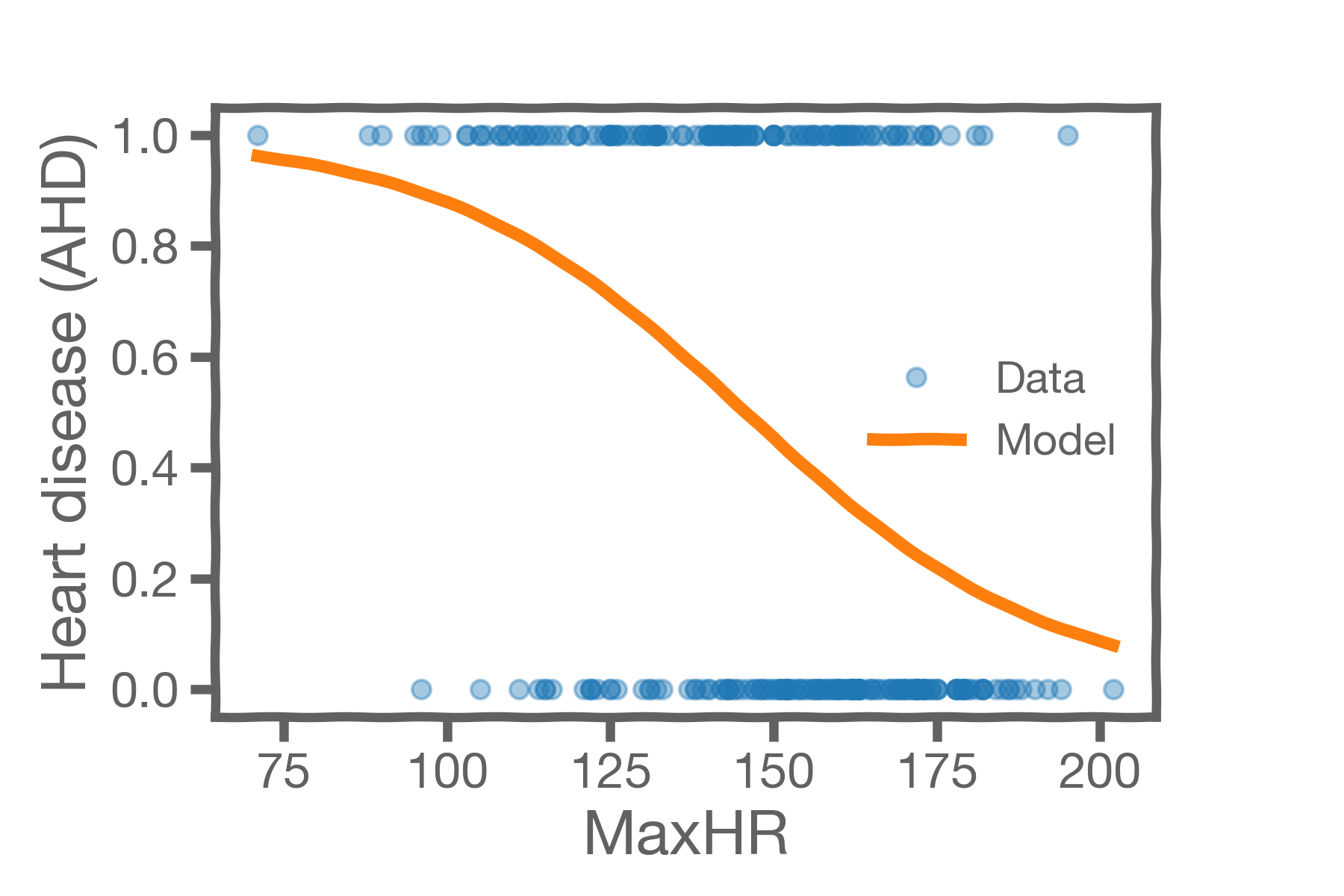
The model below can act as a classifier for the heart disease dataset which contains a lot of overlap. The height of the orange model curve represents our model's probability that a patient with that maxHR has heart disease. Notice that for a given patient's maximum heart rate close to the mean of our dataset, like 130, it is really unclear whether the patient is in fact diagnosable with heart disease. In this case, our model predicts close to 50% probability of heart disease. On the other hand, if the max heart rate is 190, our model would predict close to 10% probability of heart disease, or if the max heart rate is 85, our model would predict close to 90% probability of heart disease.

Turning model probabilities into concrete classifications— for example, declaring that a patient is a YES, NO, or MAYBE on whether or not they have heart disease— requires choosing a classification thresholds. A common threshold is 50%, (predict YES for >50% and NO for < 50%) but for certain applications it may make sense to choose a different threshold.

Let  be the probability output by our model. Because our model here contains significant overlap, it may be sensible to classify a patient as YES when , classify a patient as NO when  , and classify a patient as MAYBE when  .