自动控制原理 第四章（根轨迹法）【上】

一、根轨迹法的基本概念

1、根轨迹的基本概念

（1）根轨迹是当开环系统某一参数（如根轨迹增益，它是首1型开环传递函数对应的系数）从零变化到无穷大时，闭环特征方程的根在s平面上移动的轨迹。（根轨迹法同样适用于后面介绍的离散系统）

（2）根轨迹的意义：

2、根轨迹与系统性能

（1）稳定性：

①如果系统根轨迹全部落在左半s平面，则系统是稳定的。

②如果系统根轨迹越过虚轴进入右半s平面，则在相应K值下系统是不稳定的。

③根轨迹与虚轴交点处的K值就是临界开环增益。

（2）根轨迹与系统性能之间有着密切的联系，利用根轨迹可以分析当系统参数（K或）增大时系统动态性能的变化趋势。图解方法可以根据已知的开环零、极点迅速地绘出闭环系统的根轨迹。

3、闭环零、极点与开环零、极点之间的关系

（1）开环零、极点表示的系统闭环传递函数：

（2）由上述推导可见：

（3）根轨迹法的任务在于，由已知的开环零、极点的分布及根轨迹增益，通过图解法找出闭环极点，一旦闭环极点确定以后，再补上闭环零点，系统性能便可以确定。

4、根轨迹方程

（1）系统的闭环特征方程为，即

（2）根据幅值条件和相角条件可知，s平面上的某个点，只要满足相角条件，则该点必定在根轨迹上，至于该点所对应的，可由幅值条件得出，这意味着在s平面上满足相角条件的点必定也同时满足幅值条件，因此，相角条件是确定根轨迹s平面上一点是否在根轨迹上的充要条件。

二、绘制根轨迹的基本法则

1、法则1——根轨迹的起点和终点

（1）根轨迹起始于开环极点，终止于开环零点；当开环极点个数n大于开环零点个数m时，有n－m条根轨迹分支趋向于无穷远处。

（2）证明：

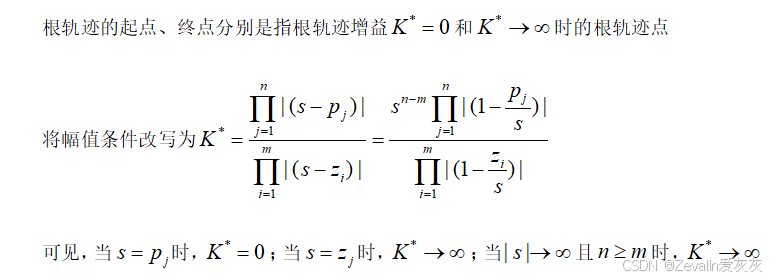
2、法则2——根轨迹的分支数，对称性和连续性

（1）根轨迹的分支数与开环零点数m、开环极点数n中的大者相等，根轨迹连续并且对称于实轴。

（2）证明：

（3）由对称性，只需画出s平面上半部和实轴上的根轨迹，下半部的根轨迹即可对称画出。

3、法则3——实轴上的根轨迹

（1）实轴上的某一区域，若其右边开环实数零、极点个数之和为奇数，则该区域一定是根轨迹。

（2）证明：

4、法则4——根之和

（1）当系统开环传递函数的分子、分母阶次差大于等于2时，系统闭环极点之和等于系统开环极点之和。

（2）证明：

（3）当时，随着的增大，若一部分极点总体向右移动，则另一部分极点必然总体上向左移动，且左、右移动的距离增量之和为0。

（4）若系统有2个开环极点，1个开环零点，且在复平面存在根轨迹，则复平面的根轨迹一定是以该零点为圆心的圆弧。

（5）举例：

5、法则5——根轨迹的渐近线

（1）当系统开环极点个数n大于开环零点个数m时，有条根轨迹分支沿着与实轴夹角为、交点为的一组渐近线趋向于无穷远处，且有

（2）证明：

（3）举例：

6、法则6——根轨迹的分离点

（1）两条或两条以上根轨迹分支在s平面上相遇又分离的分离点，其坐标d是如下方程的解。（将分离点代回特征方程或根据幅值条件可解得其对应的）

（2）举例：

（3）关于根轨迹对称性的一个定理：若开环零极点均为偶数个，且关于一条平行于虚轴的直线左右对称分布，则根轨迹一定关于该直线左右对称。

7、法则7——根轨迹与虚轴的交点

（1）若根轨迹与虚轴相交，则意味着闭环特征方程出现纯虚根，因此，可在闭环特征方程中令，然后分别令方程的实部和虚部均为零，从中求得交点的坐标值及其相应的值。（根轨迹与虚轴相交，表明系统在相应值下处于临界稳定状态，故亦可用劳斯稳定判据去求出交点的坐标值及其相应的值）

（2）举例：

8、法则8——根轨迹的起始角和终止角

（1）根轨迹离开开环复数极点处的切线与正实轴的夹角称为起始角，以表示；根轨迹进入开环复数零点处的切线与正实轴的夹角称为终止角，以表示；起始角和终止角可直接利用相角条件求出。

（2）举例：

9、综合例