Transport Polytope、可解释为联合概率的集合
使用
⟨
⋅
,
⋅
⟩
\lang \cdot , \cdot \rang
⟨⋅,⋅⟩代表Frobenius点积。对于
∑
d
:
=
{
x
∈
R
+
d
:
x
T
1
d
=
1
}
\sum_d:=\{x\in\R^d_+:x^T1_d=1\}
∑d:={x∈R+d:xT1d=1}中的两个概率向量
r
r
r和
c
c
c,将
U
(
r
,
c
)
U(r,c)
U(r,c)记为
r
r
r和
c
c
c的transport polytope,称为
d
×
d
d\times d
d×d矩阵的polyhedral集合,
1
d
1_d
1d为值全为1的d维向量
U
(
r
,
c
)
:
=
{
P
∈
R
+
d
×
d
∣
P
1
d
=
r
,
P
T
1
d
=
c
}
U(r,c):=\{P\in \R^{d\times d}_+|P1_d=r,P^T1_d=c\}
U(r,c):={P∈R+d×d∣P1d=r,PT1d=c}.
U
(
r
,
c
)
U(r,c)
U(r,c)包含所有
d
×
d
d\times d
d×d的行和列的和分别
r
r
r和
c
c
c的非负矩阵。
U
(
r
,
c
)
U(r,c)
U(r,c)的概率解释为:对于X和Y这两个取值为
{
1
,
.
.
.
,
d
}
\{1,...,d\}
{1,...,d}的多项随机变量,其分布分别为
r
r
r和
c
c
c,集合
U
(
r
,
c
)
U(r,c)
U(r,c)包含
(
X
,
Y
)
(X,Y)
(X,Y)的所有可能的联合概率。实际上,任意矩阵
P
∈
U
(
r
,
c
)
P\in U(r,c)
P∈U(r,c)与
(
X
,
Y
)
(X,Y)
(X,Y)的联合概率等价,
p
(
X
=
i
,
Y
=
j
)
=
p
i
j
p(X=i,Y=j)=p_{ij}
p(X=i,Y=j)=pij。将熵
h
h
h,
P
,
Q
∈
U
(
r
,
c
)
P,Q\in U(r,c)
P,Q∈U(r,c)的Kullback-Leibler散度和边缘参数
r
∈
∑
d
r\in \sum_d
r∈∑d记为
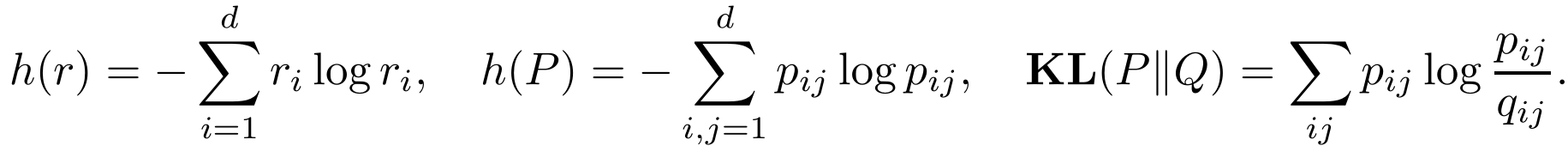
r r r和 c c c之间的最优传输
给定
d
×
d
d\times d
d×d的代价矩阵
M
M
M,从
r
r
r映射到
c
c
c的代价可以用传输矩阵(transport matrix)(或联合概率)量化为
⟨
P
,
M
⟩
\lang P, M\rang
⟨P,M⟩。
d
M
(
r
,
c
)
:
=
min
P
∈
U
(
r
,
c
)
⟨
P
,
M
⟩
\boxed{d_M(r,c):=\min_{P\in U(r,c)}\lang P,M\rang}
dM(r,c):=P∈U(r,c)min⟨P,M⟩(1)
等式(1)称作给定代价矩阵
M
M
M时,
r
r
r和
c
c
c的最优传输(OT)问题。除其他方法外,使用network simplex(Ahuja et al., 1993, §9)可以得到该问题的最优表
P
∗
P^*
P∗。当M是度量矩阵时,该问题的最优解
d
M
(
r
,
c
)
d_M(r,c)
dM(r,c)是
r
r
r和
c
c
c的距离(Villani, 2009, §6.1),称为M属于距离矩阵的锥。(Avis, 1980; Brickell et al., 2008)

在近期提出的算法之中,对于一般的矩阵
M
M
M,最优解的计算复杂度在最差情况下,范围在
O
(
d
3
log
d
)
O(d^3\log d)
O(d3logd)之间,实际上也是超立方(Pele and Werman, 2009, §2.1)






















 2086
2086











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








