在根据前面四篇文章的自抗扰控制各个功能部分的分解介绍以及对于PID算法原理的分析之后,具体可以查看我的主页。之后我们可以画出自抗扰控制的框图,并作出自抗扰的仿真了。
自抗扰的组成部分
ADRC说得更直白一些,就是PID算法的改进版本,它的许多模块都是针对PID算法的一些缺点来进行的改进。
1.对于阶跃响应,或者说初始误差较大时,PID容易难以兼顾快速性与超调之间的矛盾,或者说调试参数需要耗费非常多的时间,因此ADRC引入了跟踪微分器来输出一个过渡信号来跟踪目标信号,避免初始误差大的情况;
2.对于D项微分信号在实际中难以获取的问题,ADRC也引入跟踪微分器来输出过渡信号的微分信号作为目标微分信号,同时引入扩张状态观测器来输出反馈状态的微分信号来作为实际微分信号,它们的差值,即为ADRC的微分作用项的误差;
3.对于实际控制中的偏差,ADRC引入扩张状态观测器,人为引入非线性的偏移误差函数f来观测控制偏差并进行补偿
针对上述的三点,我们便可以画出ADRC的框图:

可以看到,在上一篇文章中,根据ADRC的思想去改进PID的框图与这个很像,只是把反馈状态的跟踪微分器替换成了扩张状态观测器,由观测器去输出反馈信号与反馈微分信号,并且输出一个扰动信号z3,之后将控制扰动 z3 加到控制器的输出 u0 上,再除以系统的控制器增益b0,得到最终的控制器输出。注意:在将 u 传入观测器时需要乘以控制器的增益 b0 ,同样的,观测器输出的扰动 z3 在增加到控制器输出 u0 上之后,也要除以这个增益 b0 ,一般来说有两种形式:
u = u0 - z3/b0 或 u = (u0 - z3) / b0
两种都可以,我画的是其中一种,不过一般来说,我这里都把 b0 置1了,所以简化了一些。之后可以搭建其模型:
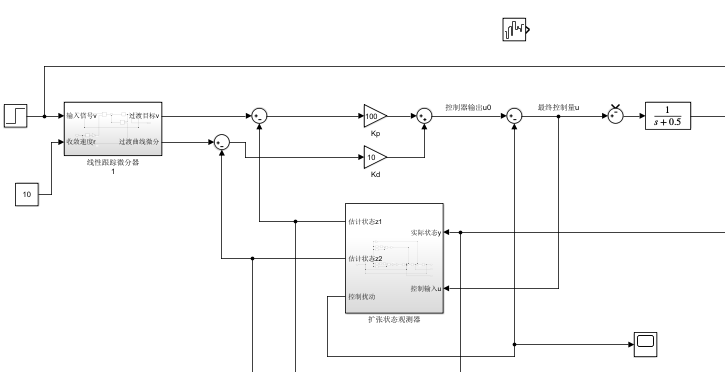
同时我又搞了一个PID的,尝试将两者都调到同样的响应,看一下调试难度。
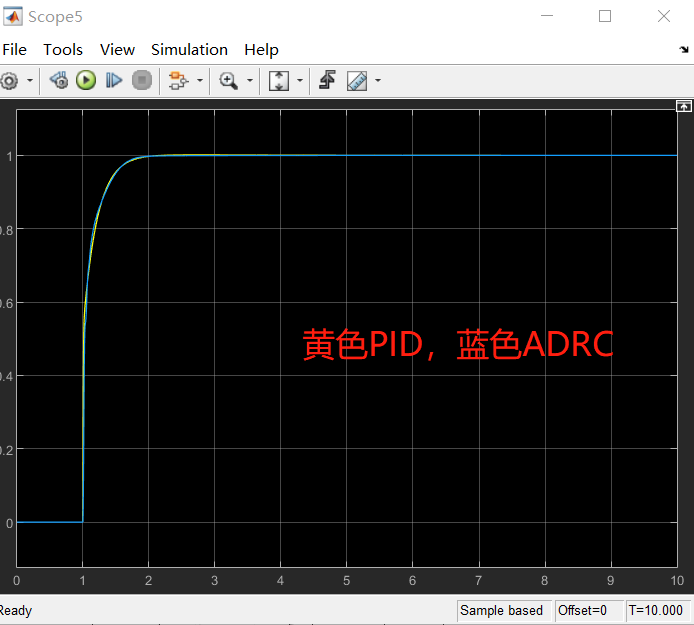
上面是调试出PID与ADRC相同的曲线,其实花费时间的话,都差不多,尤其是增快响应速度的时候,不过如果是单纯的增快速度的话,PID调起来会更快一些,但是确实容易带来超调,这时候就要找到Kp与Kd的平衡,抑制超调,ADRC的效果总体来说会平稳许多,但是ADRC调试比较耗费时间的是加快响应的过程,整体来说,ADRC的参数一般给到一个范围,基本都不会超调,都比较平稳。
那么这时候问题就来了,ADRC的优势在哪里,如果是PID使劲调,把传感器的微分测量也做得比较好,也可以达到这样效果的话,为何要用ADRC呢?此时我们把ADRC与PID的参数都保持不变,将控制上增加一个白噪声,就可以看出一些区别:


可以看到ADRC的抗扰能力要更好一些,我这里增加的扰动量(白噪声)的大小与频率都是相同的。具体的话,我后续会实际搞一个控制对象来测试实际的东西。








 本文详细介绍了自抗扰控制(ADRC)的组成部分,包括跟踪微分器、扩张状态观测器及其对PID算法的改进。通过ADRC与PID的框图对比和仿真,展示了ADRC在阶跃响应、微分信号获取和偏差补偿方面的优势。尽管ADRC的参数调试可能更为耗时,但其在抗扰动能力和系统稳定性上的表现优于PID。在引入白噪声的仿真中,ADRC展现出更好的抗扰能力。文章最后提出了ADRC在实际控制系统中的应用潜力。
本文详细介绍了自抗扰控制(ADRC)的组成部分,包括跟踪微分器、扩张状态观测器及其对PID算法的改进。通过ADRC与PID的框图对比和仿真,展示了ADRC在阶跃响应、微分信号获取和偏差补偿方面的优势。尽管ADRC的参数调试可能更为耗时,但其在抗扰动能力和系统稳定性上的表现优于PID。在引入白噪声的仿真中,ADRC展现出更好的抗扰能力。文章最后提出了ADRC在实际控制系统中的应用潜力。

















 7115
7115

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








