Horn-Schunck Method

Horn-Schunck method is a global method which introduces a global constraint of smoothness to solve the aperture problem in Optical Flow.

The flow is formulated as a global energy functional which is then sought to be minimized.

$$E(u,v)=\int \int [(I_{x}u+I_{y}v+I_t{)}^2+{\alpha }^2(||\nabla u|{|}^2+||\nabla v|{|}^2)]dxdy$$
Because
$$\left[\begin{array}{c}u\\ v\end{array}\right]=f(\left[\begin{array}{c}x\\ y\end{array}\right])$$
By multi-dimensional Euler-Lagrange equation:
$$\frac{\partial L}{\partial u}-\frac{\partial }{\partial x}\frac{\partial L}{\partial u_x}-\frac{\partial }{\partial y}\frac{\partial L}{\partial u_y}=0$$

$$\frac{\partial L}{\partial v}-\frac{\partial }{\partial x}\frac{\partial L}{\partial v_x}-\frac{\partial }{\partial y}\frac{\partial L}{\partial v_y}=0$$

Because
$$L=(I_{x}u+I_{y}v+I_t{)}^2+{\alpha }^2(u_x^2+u_y^2+v_x^2+v_y^2)dxdy$$

So we then have
$$I_x(I_{x}u+I_{y}v+I_t)-{\alpha }^2(\frac{\partial u_x}{\partial x}+\frac{\partial u_y}{\partial x})=0$$

$$I_y(I_{x}u+I_{y}v+I_t)-{\alpha }^2(\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial x})=0$$

which leads to
$$\begin{array}{r}{I}_x(I_{x}u+I_{y}v+I_t)-{\alpha }^2\Delta u=0\\ I_y(I_{x}u+I_{y}v+I_t)-{\alpha }^2\Delta v=0\end{array}$$

$\Delta =\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}$ with the operator
$$\left[\begin{array}{ccc}0& 1/4& 0\\ 1/4& -1& 1/4\\ 0& 1/4& 0\end{array}\right]or\left[\begin{array}{ccc}0& -1/4& 0\\ -1/4& 1& -1/4\\ 0& -1/4& 0\end{array}\right]$$

i.e.
$$f_{xx}+f_{yy}=f_{center}-f_{average}$$

replace $\Delta u$ and $\Delta v$, we get the discrete version
$$\begin{gathered} I_x(I_{x}u+I_{y}v+I_t)-{\alpha }^2(u-u_{avg})=0 \\ {I}_y(I_{x}u+I_{y}v+I_t)-{\alpha }^2(v-v_{avg})=0 \end{gathered}$$

Iteration

However, since the solution depends on the neighboring values of the flow field: $\Delta u,\Delta v$, it must be repeated once the neighbors have been updated. The following iterative scheme is derived:

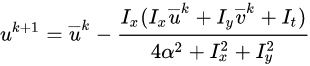
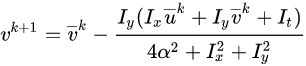
where the superscript k+1 denotes the next iteration, which is to be calculated and k is the last calculated result.

TODO

This is in essence a Matrix splitting method, similar to the Jacobi method, applied to the large, sparse system arising when solving for all pixels simultaneously.