第二章 数列极限

数列极限的定义

这个x->∞ 我们认为是+-无穷与这个n不一样

性质	数列极限	函数极限
唯一性	唯一	唯一
有界性	全局有界（所有项有界）	局部有界（某邻域内有界）
保号性	尾部保号（从某 N 开始）	局部保号（某邻域内保号）

1. 唯一性（相同点）

• 数列极限：若数列 {an} 收敛，则它的极限唯一。例如，若 lim⁡n→∞an=A，则 A 是唯一的。

• 函数极限：若函数 f(x) 当 x→0（或 x→∞）时的极限存在，则极限值唯一。例如，若 lim⁡x→x0 f(x)=A则 A 唯一。

共同本质：无论数列还是函数，极限值若存在，必唯一。

2. 有界性（不同点）

• 数列极限的全局有界性：
  若数列 {an}收敛，则整个数列有界，即存在常数 M>0，使得对所有项都有 ∣an∣≤M。
  例子：数列 an=1/n 收敛于 0，且所有项满足 ∣an∣≤1。

• 函数极限的局部有界性：
  若 lim⁡x→x0f(x)=A，则存在 x0的某个去心邻域（如 0<∣x−x0∣<δ），使得在此邻域内 f(x)有界，即 ∣f(x)∣≤M。
  例子：f(x)=sin⁡(1/x)在 x→0时极限不存在，但若极限存在（如 f(x)=x在 x→1时），则在 x=1附近有界，但整体可能无界。

关键区别：
数列的收敛性保证所有项有界（全局），而函数仅保证极限点附近有界（局部）。

3. 保号性（不同点）

• 数列极限的保号性：
  若 lim⁡n→∞an=A>0（或 A<0），则存在正整数 N，当 n>N时，an>0（或an​<0）。
  

• 函数极限的局部保号性：
  若 lim⁡x→x0f(x)=A>0（或 A<0），则存在 x0​ 的某个去心邻域，使得在此邻域内 f(x)>0（或 f(x)<0）。
  例子：函数 f(x)=x^2 在 x→0时极限为 0，但若极限非零（如 f(x)=x在 x→1时），则在 x=1附近 f(x)>0。

去帽子严格

关键区别：
数列的保号性从某个 N 开始（离散的“尾部”），而函数的保号性在某个邻域内成立（连续的局部区域）。

定义

        这两个定义非常相似，都是用 ε 来描述趋近的过程。数列极限是针对离散的 n，而函数极限是针对连续的 x。数列的 n 只能取正整数，而函数的 x 可以取任意实数。

数列收敛与其子列收敛的关系

海涅定理 （归结原则）

• 为什么用海涅定理：数列是离散的，无法直接用求导工具（如洛必达），但转为函数后可以。

• 定理核心：函数极限存在 ⇨ 所有相关数列的极限相同，反之亦然。

        当计算数列的极限困难时，可以将数列看作函数的一部分，先求出对应的函数极限，再利用这个定理得出数列的极限值。它的核心思想是：如果所有趋近于某点的数列，对应的函数值都收敛到同一个数，那么函数的极限就是这个数；反之亦然。

        如果一个函数在某个点的极限存在，那么无论用什么样的数列趋近于这个点，函数在这个数列上的极限都应该和函数在该点的极限相同。以上例子说明f(x)在一点处连续，并不意味着f(x)在这点的附近连续。

夹b准则

放缩的常用方法如下

• 已知方法
• 未知方法（题设给出）一般第一问

(1)利用简单的放大与缩小

第一个不等式的下界依赖于最小值，可能极低（如接近 0），则 n⋅umin可趋近于 0，使得总和的下界极低，范围更广；

而第二个不等式的下界由最大值固定，约束更严格。

因此，第二个不等式是“有限的”（范围更窄），而第一个是“无限的”（范围更广）。

(2)利用重要不等式

绝对值不等式：

• ∣a±b∣≤∣a∣+∣b∣

• ∣∣a∣−∣b∣∣≤∣a−b∣

• 推广到 n 个实数:∣a1​±a2​±⋯±an​∣≤∣a1​∣+∣a2​∣+⋯+∣an​∣

均值不等式

 几何平均数小于或等于它们的算术平均数

  ​​​​​指数不等式：

分数的不等式

三角不等式

⑩⑪⑫

⑫中值定理可得

(3)利用闭区间上连续函数必有最大值与最小值

(4)利用压缩映射原理。（简化版）

        核心思想是：如果每次迭代后的误差（与目标值的距离）都比前一步按固定比例缩小，那么数列最终会收敛到目标值。也就是原理一

        函数 f(x) 有一个不动点 a，并且在所有点上，它的斜率（导数）的绝对值都不超过 k<1。这意味着，无论从哪里开始，每一步应用 f(x)，新的点都会比前一个点更接近 a，因为斜率的绝对值小于 1，所以距离会减少。

例子：

        假设我们有函数 f(x)=0.5​x+1。首先，找到它的不动点 a，即解方程 a=0.5​a+1。所以，不动点是 a=2。

接下来，计算导数f′(x)=0.5​。因为 ∣f′(x)∣=0.5​<1所以满足原理二的条件。

现在，假设我们从 x1​=0 开始，生成数列：

---

        假设你每次调整数值时，误差都会打一个折扣（比如每次都减少一半）。只要折扣力度足够大（折扣因子在0到1之间），经过无数次调整后，误差会变得无限小，最终精确命中目标。

现在，假设我们从 x1​=5 开始

(5)利用题设条件来推证(这往往是解答题的第1问

例题

(1)利用简单的放大与缩小

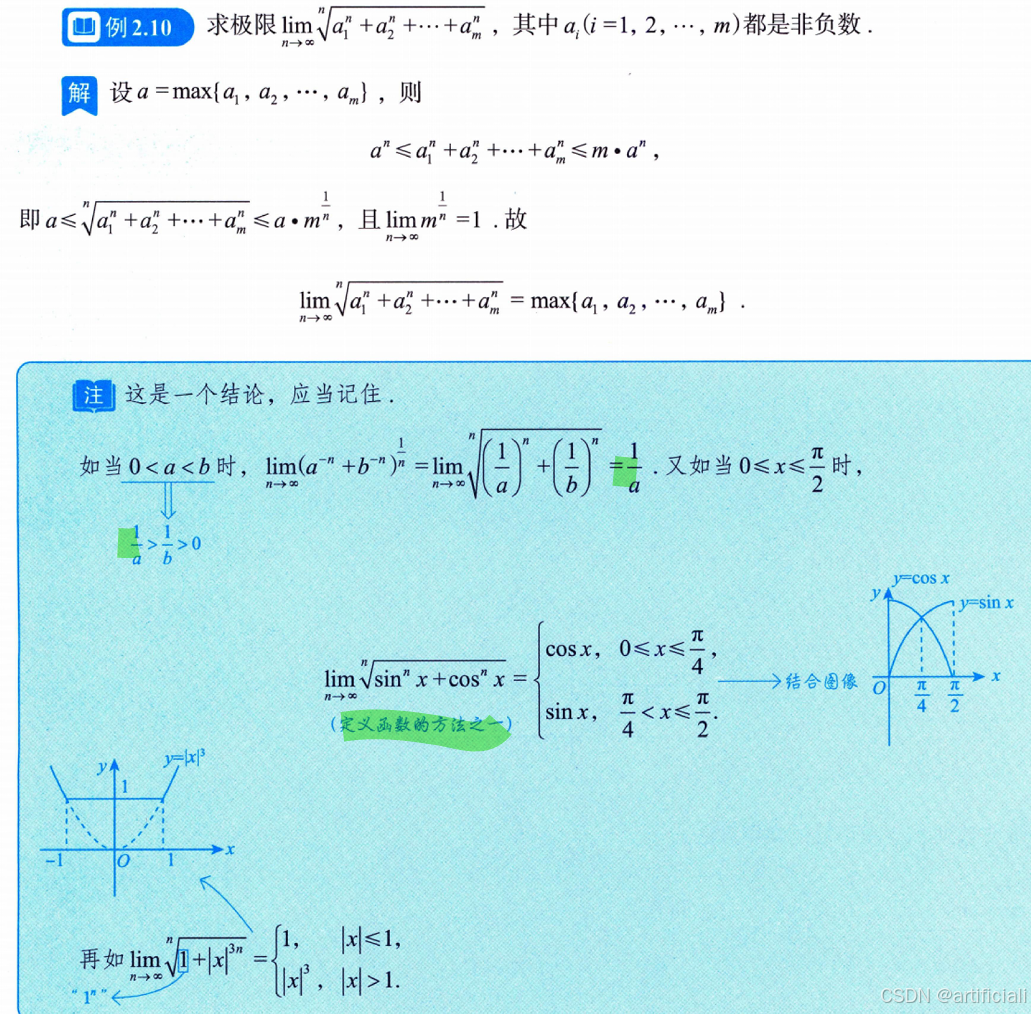
单调有界准则（单调有界准则是讨论数列极限存在的两个最重要的准则之一，另外一个是夹逼准则）

我们判断是否极限存在，先看判断单调，再看界限：

如何看单调：

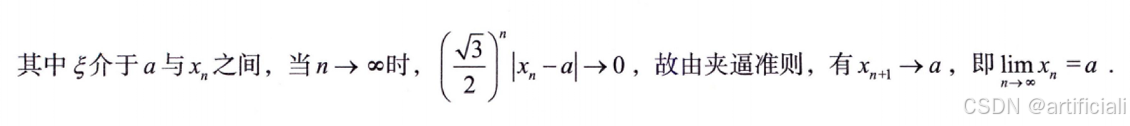
{Xn}收敛于a的速度问题