第2讲 基于优化的 IMU 与视觉信息融合
1.最小二乘问题求解
(1)最小二乘基础概念
1 定义:找到一个n维的变量 x∈Rnx \in R^nx∈Rn ,使得损失函数 F(x)F(x)F(x) 取得局部最小值:
F(x)=12∑i=1m(fi(x))2
F(x) = \frac{1}{2} \sum_{i=1}^m (f_i(x))^2
F(x)=21i=1∑m(fi(x))2
2 cost function 泰勒展开
F(x+Δx)=F(x)+JΔx+12ΔxTHΔx+O(∣∣Δx∣∣3) F(x + \Delta x) = F(x) + J \Delta x + \frac{1}{2} \Delta x^TH \Delta x + O(||\Delta x||^3) F(x+Δx)=F(x)+JΔx+21ΔxTHΔx+O(∣∣Δx∣∣3)
3 迭代法
找一个下降方向使得损失函数随x的迭代逐渐减小,直到x收敛到 x∗x^*x∗:
F(xk+1)<F(xk)
F(x_{k+1}) < F(x_k)
F(xk+1)<F(xk)
第一步:找下降方向单位向量 d,第二步:确定下降步长 α\alphaα
假设 α\alphaα 足够小,对 F(x)F(x)F(x) 进行一阶泰勒展开:
F(x+αd)≈F(x)+αJd
F(x+ \alpha d) \thickapprox F(x) + \alpha Jd
F(x+αd)≈F(x)+αJd
所以只需要寻找下降方向,满足:
Jd<0
Jd < 0
Jd<0
(2)最速下降法和牛顿法
1)最速下降法
下降方向的条件:$Jd = ||J||cos\theta $ ,θ\thetaθ 表示下降方向和梯度方向的夹角。当 θ=π\theta = \piθ=π时:
d=−JT∣∣J∣∣
d = \frac{-J^T}{||J||}
d=∣∣J∣∣−JT
即梯度的负方向为最速下降方向。
2)牛顿法
J+HΔx=0=>HΔx=−J
J+H \Delta x = 0 \\
=> H \Delta x = -J
J+HΔx=0=>HΔx=−J
求解线性方程,便得到了增量。
3)阻尼法
记:
F(x+Δx)≈L(Δx)≡F(x)+JΔx+12ΔxTHΔx
F(x + \Delta x) \thickapprox L(\Delta x) \equiv F(x) + J\Delta x + \frac{1}{2}\Delta x^TH\Delta x
F(x+Δx)≈L(Δx)≡F(x)+JΔx+21ΔxTHΔx
求以下函数的最小化:
Δx≡arg min{L(Δx)+12μΔxTΔx}
\Delta x \equiv arg\;min\{L(\Delta x) + \frac{1}{2}\mu \Delta x^T \Delta x \}
Δx≡argmin{L(Δx)+21μΔxTΔx}
求导,并整理:
(H+μI)Δx=−JT (H + \mu I) \Delta x = -J^T (H+μI)Δx=−JT
(3)高斯牛顿法
(JTJ)Δx=−JTf=>HΔx=b (J^TJ)\Delta x = -J^T f \\ => H \Delta x = b (JTJ)Δx=−JTf=>HΔx=b
(4)LM
对高斯牛顿法进行了改进,求解过程中引入了阻尼因子:
(JTJ+μI)Δx=−JTf μ>0
(J^TJ + \mu I)\Delta x = -J^Tf \;\;\;\;\;\; \mu > 0
(JTJ+μI)Δx=−JTfμ>0
阻尼因子 μ\muμ 的作用:
1 μ>0\mu > 0μ>0 保证迭代朝着下降方向
2 μ\muμ 非常大,则 Δx=−1μJTf=−1μF′(x)T\Delta x = -\frac{1}{\mu} J^T f = -\frac{1}{\mu}F^ \prime (x)^TΔx=−μ1JTf=−μ1F′(x)T,接近最速下降法
3 μ\muμ 非常小,则 接近高斯牛顿法
简单的 μ0\mu_0μ0 初始值选取策略:
μ0=τ max{(JTJ)ii}
\mu_0 = \tau \;max\{(J^TJ)_{ii} \}
μ0=τmax{(JTJ)ii}
通常,τ∈[10−8,1]\tau \in [10^{-8}, 1]τ∈[10−8,1]
阻尼因子 μ\muμ 的更新策略:
定义比例因子
ρ=F(x)−F(x+Δx)L(0)−L(Δx)L(0)−L(Δx)=12ΔxT(μΔx−JTf)
\rho = \frac{F(x) - F(x + \Delta x)}{L(0) - L(\Delta x)} \\
L(0) - L(\Delta x) = \frac{1}{2}\Delta x^T(\mu \Delta x - J^Tf)
ρ=L(0)−L(Δx)F(x)−F(x+Δx)L(0)−L(Δx)=21ΔxT(μΔx−JTf)
Marquardt 策略
if ρ<0.25μ:=u∗2else if ρ>0.75μ:=μ/3
if \;\; \rho < 0.25 \\
\mu :=u * 2 \\
else\;\; if\;\;\rho > 0.75\\
\mu :=\mu/3
ifρ<0.25μ:=u∗2elseifρ>0.75μ:=μ/3
Nielsen策略
if ρ>0μ:=u∗max{13,1−(2ρ−1)3}; v:=2else μ:=μ∗3;v:=2∗v
if \;\; \rho > 0\\
\mu :=u * max\{\frac{1}{3}, 1-(2\rho-1)^3 \}; \;\; v :=2\\
else\;\;\;\;\;\;\;\;\;\\
\mu :=\mu * 3; v:=2*v
ifρ>0μ:=u∗max{31,1−(2ρ−1)3};v:=2elseμ:=μ∗3;v:=2∗v
Nielsen策略实现代码:
/// LM
void Problem::ComputeLambdaInitLM() {
ni_ = 2.;
currentLambda_ = -1.;
currentChi_ = 0.0;
// TODO:: robust cost chi2
for (auto edge: edges_) {
currentChi_ += edge.second->Chi2();
}
if (err_prior_.rows() > 0)
currentChi_ += err_prior_.norm();
stopThresholdLM_ = 1e-6 * currentChi_; // 迭代条件为 误差下降 1e-6 倍
double maxDiagonal = 0;
ulong size = Hessian_.cols();
assert(Hessian_.rows() == Hessian_.cols() && "Hessian is not square");
for (ulong i = 0; i < size; ++i) {
maxDiagonal = std::max(fabs(Hessian_(i, i)), maxDiagonal);
}
double tau = 1e-5;
currentLambda_ = tau * maxDiagonal;
}
void Problem::AddLambdatoHessianLM() {
ulong size = Hessian_.cols();
assert(Hessian_.rows() == Hessian_.cols() && "Hessian is not square");
for (ulong i = 0; i < size; ++i) {
Hessian_(i, i) += currentLambda_;
}
}
void Problem::RemoveLambdaHessianLM() {
ulong size = Hessian_.cols();
assert(Hessian_.rows() == Hessian_.cols() && "Hessian is not square");
// TODO:: 这里不应该减去一个,数值的反复加减容易造成数值精度出问题?而应该保存叠加lambda前的值,在这里直接赋值
for (ulong i = 0; i < size; ++i) {
Hessian_(i, i) -= currentLambda_;
}
}
bool Problem::IsGoodStepInLM() {
double scale = 0;
scale = delta_x_.transpose() * (currentLambda_ * delta_x_ + b_);
scale += 1e-3; // make sure it's non-zero :)
// recompute residuals after update state
// 统计所有的残差
double tempChi = 0.0;
for (auto edge: edges_) {
edge.second->ComputeResidual();
tempChi += edge.second->Chi2();
}
double rho = (currentChi_ - tempChi) / scale;
if (rho > 0 && isfinite(tempChi)) // last step was good, 误差在下降
{
double alpha = 1. - pow((2 * rho - 1), 3);
alpha = std::min(alpha, 2. / 3.);
double scaleFactor = (std::max)(1. / 3., alpha);
currentLambda_ *= scaleFactor;
ni_ = 2;
currentChi_ = tempChi;
return true;
} else {
currentLambda_ *= ni_;
ni_ *= 2;
return false;
}
}
(5)鲁棒核函数
2. VIO残差函数的构建
(1)系统需要优化的状态量
χ=[xn,xn+1,⋯ ,xn+N,λm,λm+1,λm+M]xi=[pwbi,qwbi,viw,babi,bgbi],i∈[n,n+N] \chi = [x_n, x_{n+1}, \cdots, x_{n+N}, \lambda_m, \lambda_{m+1}, \lambda_{m+M}]\\ x_i = [p_{wb_i}, q_{wb_i}, v_i^w, b_a^{b_i}, b_g^{b_i}] , i \in[n, n+N] χ=[xn,xn+1,⋯,xn+N,λm,λm+1,λm+M]xi=[pwbi,qwbi,viw,babi,bgbi],i∈[n,n+N]
其中: xix_ixi 包含 iii 时刻IMU机体在惯性坐标系中的位置,姿态,速度以及IMU机体坐标系中的加速度和角速度的偏置量估计;
n,mn, mn,m 分别是机体状态量,路标在滑动窗口里的起始时刻;
N 滑动窗口中关键帧数量;
M 被滑动窗口内所有关键帧观测到的;路标数量。
(2)基于逆深度的重投影误差
特征点逆深度在第 iii 帧中初始化得到,在第 jjj 帧又被观测到,预测其在第 jjj 帧中的坐标:
[xcj,ycj,zcj,1]T=Tbc−1Twbj−1TwbiTbc[1λuci,1λvci,1λ,1]T
[x_{c_j}, y_{c_j}, z_{c_j}, 1]^T = T_{bc}^{-1} T_{wb_j}^{-1} T_{wb_i}T_{bc}[\frac{1}{\lambda}u_{c_i}, \frac{1}{\lambda}v_{c_i}, \frac{1}{\lambda}, 1]^T
[xcj,ycj,zcj,1]T=Tbc−1Twbj−1TwbiTbc[λ1uci,λ1vci,λ1,1]T
思考公式的含义:本质上还是相机那一套,只不过IMU的 body 坐标系充当了一个桥梁的作用。(上个时刻的计算得到的像素坐标通过上个时刻的逆深度来估计此时刻的3维世界坐标值)
(3)IMU预积分
pwbj=pwbi+viwΔt−12gwΔt2+qwbi∬t∈[i,j](qbibtabt)δt2⏟α \mathbf{p}_{w b_{j}}=\mathbf{p}_{w b_{i}}+\mathbf{v}_{i}^{w} \Delta t-\frac{1}{2} \mathbf{g}^{w} \Delta t^{2}+\mathbf{q}_{w b_{i}} \underbrace{\iint_{t \in[i, j]}\left(\mathbf{q}_{b_{i} b_{t}} \mathbf{a}^{b_{t}}\right) \delta t^{2}}_{\mathbf{\alpha}} pwbj=pwbi+viwΔt−21gwΔt2+qwbiα∬t∈[i,j](qbibtabt)δt2
vjw=viw−gwΔt+qwbi∫t∈[i,j](qbibtabt)δt⏟β \mathbf{v}_{j}^{w}=\mathbf{v}_{i}^{w}-\mathbf{g}^{w} \Delta t+\mathbf{q}_{w b_{i}}\underbrace{\int_{t \in[i, j]}\left(\mathbf{q}_{b_{i} b_{t}} \mathbf{a}^{b_{t}}\right) \delta t}_{\mathbf{\beta}} vjw=viw−gwΔt+qwbiβ∫t∈[i,j](qbibtabt)δt
qwbj=qwbi∫t∈[i,j]qbibt⊗[012ωbt]δt⏟γ \mathbf{q}_{w b_{j}}=\mathbf{q}_{w b_{i}}\underbrace{\int_{t \in[i, j]} \mathbf{q}_{b_{i} b_{t}} \otimes\left[\begin{array}{c}0 \\ \frac{1}{2} \boldsymbol{\omega}^{b_{t}}\end{array}\right] \delta t}_{\mathbf{\gamma}} qwbj=qwbiγ∫t∈[i,j]qbibt⊗[021ωbt]δt
预积分量:
αbibj=∬t∈[i,j](qbibtabt)δt2
\boldsymbol{\alpha}_{b_{i} b_{j}}=\iint_{t \in[i, j]}\left(\mathbf{q}_{b_{i} b_{t}} \mathbf{a}^{b_{t}}\right) \delta t^{2}
αbibj=∬t∈[i,j](qbibtabt)δt2
βbibj=∫t∈[i,j](qbibtabt)δt \boldsymbol{\beta}_{b_{i} b_{j}}=\int_{t \in[i, j]}\left(\mathbf{q}_{b_{i} b_{t}} \mathbf{a}^{b_{t}}\right) \delta t βbibj=∫t∈[i,j](qbibtabt)δt
qbibj=∫t∈[i,j]qbibt⊗[012ωbt]δt \mathbf{q}_{b_{i} b_{j}}=\int_{t \in[i, j]} \mathbf{q}_{b_{i} b_{t}} \otimes \left[ \begin{array}{c} 0 \\ \frac{1}{2} \boldsymbol{\omega}^{b_{t}} \end{array} \right] \delta t qbibj=∫t∈[i,j]qbibt⊗[021ωbt]δt
基于预积分量的导航状态更新公式:
[pwbjvjwqwbjbjabjg]=[pwbi+viwΔt−12gwΔt2+qwbiαbibjviw−gwΔt+qwbiβbibjqwbiqbibjbiabig] \left[ \begin{array}{c} \mathbf{p}_{w b_{j}} \\ \mathbf{v}_{j}^{w} \\ \mathbf{q}_{w b_{j}} \\ \mathbf{b}_{j}^{a} \\ \mathbf{b}_{j}^{g} \end{array} \right] =\left[ \begin{array}{c} \mathbf{p}_{w b_{i}}+\mathbf{v}_{i}^{w} \Delta t-\frac{1}{2} \mathbf{g}^{w} \Delta t^{2}+\mathbf{q}_{w b_{i}} \boldsymbol{\alpha}_{b_{i} b_{j}} \\ \mathbf{v}_{i}^{w}-\mathbf{g}^{w} \Delta t+\mathbf{q}_{w b_{i}} \boldsymbol{\beta}_{b_{i} b_{j}} \\ \mathbf{q}_{w b_{i}} \mathbf{q}_{b_{i} b_{j}} \\ \mathbf{b}_{i}^{a} \\ \mathbf{b}_{i}^{g} \end{array} \right] ⎣⎡pwbjvjwqwbjbjabjg⎦⎤=⎣⎡pwbi+viwΔt−21gwΔt2+qwbiαbibjviw−gwΔt+qwbiβbibjqwbiqbibjbiabig⎦⎤
(4)预积分误差
(5)预积分的离散形式
采用中值积分法
ω=12[(ωbk−bkg)+(ωbk+1−bkg)]
\boldsymbol{\omega}=\frac{1}{2}\left[\left(\boldsymbol{\omega}^{b_{k}}-\mathbf{b}_{k}^{g}\right)+\left(\boldsymbol{\omega}^{b_{k+1}}-\mathbf{b}_{k}^{g}\right)\right]
ω=21[(ωbk−bkg)+(ωbk+1−bkg)]
a=12[qbibk(abk−bka)+qbibk+1(abk+1−bka)] \mathbf{a}=\frac{1}{2}\left[\mathbf{q}_{b_{i} b_{k}}\left(\mathbf{a}^{b_{k}}-\mathbf{b}_{k}^{a}\right)+\mathbf{q}_{b_{i} b_{k+1}}\left(\mathbf{a}^{b_{k+1}}-\mathbf{b}_{k}^{a}\right)\right] a=21[qbibk(abk−bka)+qbibk+1(abk+1−bka)]
αbibk+1=αbibk+βbibkδt+12aδt2 \boldsymbol{\alpha}_{b_{i} b_{k+1}}=\boldsymbol{\alpha}_{b_{i} b_{k}}+\boldsymbol{\beta}_{b_{i} b_{k}} \delta t+\frac{1}{2} \mathbf{a} \delta t^{2} αbibk+1=αbibk+βbibkδt+21aδt2
βbibk+1=βbibk+aδt \boldsymbol{\beta}_{b_{i} b_{k+1}}=\boldsymbol{\beta}_{b_{i} b_{k}}+\mathbf{a} \delta t βbibk+1=βbibk+aδt
qbibk+1=qbibk⊗[112ωδt] \mathbf{q}_{b_{i} b_{k+1}}=\mathbf{q}_{b_{i} b_{k}} \otimes \left[ \begin{array}{c} 1 \\ \frac{1}{2} \boldsymbol{\omega} \delta t \end{array} \right] qbibk+1=qbibk⊗[121ωδt]
bk+1a=bka+nbkaδt b_{k+1}^a = b_k^a + n_{b_k^a} \delta t bk+1a=bka+nbkaδt
bk+1g=bkg+nbkgδt b_{k+1}^g = b_k^g + n_{b_k^g} \delta t bk+1g=bkg+nbkgδt
(6)预积分量的方差
误差的传递由两部分组成:当前时刻的误差传递给下一时刻,当前时刻的测量噪声传递给下一时刻。
假设已知相邻时刻误差的线性传递方程:
ηik=Fk−1ηik−1+Gk−1nk−1
\eta_{ik} = F_{k-1}\eta_{ik-1} + G_{k-1}n_{k-1}
ηik=Fk−1ηik−1+Gk−1nk−1
其中:状态误差为 ηik=[δθik,δvik,δpik]\eta_{ik} = [\delta \theta_{ik}, \delta v_{ik}, \delta p_{ik}]ηik=[δθik,δvik,δpik],测量噪声为 nk=[nKg,nka]n_k = [n_K^g, n_k^a]nk=[nKg,nka]
预积分量的协方差矩阵通过递推得到:
Σi,k=Fk−1Σi,k−1Fk−1⊤+Gk−1ΣnGk−1⊤
\boldsymbol{\Sigma}_{i, k}=\mathbf{F}_{k-1} \boldsymbol{\Sigma}_{i, k-1} \mathbf{F}_{k-1}^{\top}+\mathbf{G}_{k-1} \boldsymbol{\Sigma_n} \mathbf{G}_{k-1}^{\top}
Σi,k=Fk−1Σi,k−1Fk−1⊤+Gk−1ΣnGk−1⊤
其中:Σn\Sigma_nΣn 为测量噪声的协方差矩阵,方差从 iii 时刻开始递推,F,G是离散时间下的状态转移矩阵
现在需要求F和G
(7)预积分微分方程
基于误差时间变化的递推方程
已知连续时间下的微分方程形式为:
X˙=FtX+GtN
\dot{\boldsymbol{X}}=\boldsymbol{F}_{t} \boldsymbol{X}+\boldsymbol{G}_{t} \boldsymbol{N}
X˙=FtX+GtN
其中:
X=[δαtbkδθtbkδβtbkδbatδbwt]
\boldsymbol{X}=
\left[
\begin{array}{l}
\delta \boldsymbol{\alpha}_{t}^{b_{k}} \\
\delta \boldsymbol{\theta}_{t}^{b_{k}} \\
\delta \boldsymbol{\beta}_{t}^{b_{k}} \\
\delta \boldsymbol{b}_{a_{t}} \\
\delta \boldsymbol{b}_{w_{t}}
\end{array}
\right]
X=⎣⎡δαtbkδθtbkδβtbkδbatδbwt⎦⎤
N=[nanwnbanbw] \boldsymbol{N}= \left[ \begin{array}{l} \boldsymbol{n}_{a} \\ \boldsymbol{n}_{w} \\ \boldsymbol{n}_{b_{a}} \\ \boldsymbol{n}_{b_{w}} \end{array} \right] N=⎣⎡nanwnbanbw⎦⎤
不推了,暂时只记结论:
δθ˙=−[ωt−bωt]×δθ+nω−δbωt
\delta \dot{\boldsymbol{\theta}}=-\left[\boldsymbol{\omega}_{t}-\boldsymbol{b}_{\omega_{t}}\right]_{\times} \delta \boldsymbol{\theta}+\boldsymbol{n}_{\omega}-\delta \boldsymbol{b}_{\omega_{t}}
δθ˙=−[ωt−bωt]×δθ+nω−δbωt
δβ˙=Rt[δθ]×(at−bat)+Rt(na−δbat)=−Rt[at−bat]×δθ+Rt(na−δbat) \begin{aligned}\delta \dot{\boldsymbol{\beta}}=\boldsymbol{R}_{t}[\delta \boldsymbol{\theta}]_{\times}\left(\boldsymbol{a}_{t}-\boldsymbol{b}_{a_{t}}\right)+\boldsymbol{R}_{t}\left(\boldsymbol{n}_{a}-\delta \boldsymbol{b}_{a_{t}}\right) \\ =-\boldsymbol{R}_{t}\left[\boldsymbol{a}_{t}-\boldsymbol{b}_{a_{t}}\right]_{\times} \delta \boldsymbol{\theta}+\boldsymbol{R}_{t}\left(\boldsymbol{n}_{a}-\delta \boldsymbol{b}_{a_{t}}\right) \end{aligned} δβ˙=Rt[δθ]×(at−bat)+Rt(na−δbat)=−Rt[at−bat]×δθ+Rt(na−δbat)
δα˙=δβ \delta \dot{\boldsymbol{\alpha}}=\delta \boldsymbol{\beta} δα˙=δβ
(8)预积分离散时间递推方程
Xk+1=FkXk+GkNk \boldsymbol{X}_{k+1}=\boldsymbol{F}_{k} \boldsymbol{X}_{k}+\boldsymbol{G}_{k} \boldsymbol{N}_{k} Xk+1=FkXk+GkNk
其中:
Xk+1=[δαk+1δθk+1δβk+1δbak+1δbωk+1]Xk=[δαkδθkδβkδbakδbωk]Nk=[naknwknak+1nwk+1nbanbw]
\boldsymbol{X}_{k+1}=\left[\begin{array}{c}
\delta \boldsymbol{\alpha}_{k+1} \\
\delta \boldsymbol{\theta}_{k+1} \\
\delta \boldsymbol{\beta}_{k+1} \\
\delta \boldsymbol{b}_{a_{k+1}} \\
\delta \boldsymbol{b}_{\omega_{k+1}}
\end{array}\right] \quad \boldsymbol{X}_{k}=\left[\begin{array}{c}
\delta \boldsymbol{\alpha}_{k} \\
\delta \boldsymbol{\theta}_{k} \\
\delta \boldsymbol{\beta}_{k} \\
\delta \boldsymbol{b}_{a_{k}} \\
\delta \boldsymbol{b}_{\omega_{k}}
\end{array}\right] \quad \boldsymbol{N}_{k}=\left[\begin{array}{c}
\boldsymbol{n}_{a_{k}} \\
\boldsymbol{n}_{w_{k}} \\
\boldsymbol{n}_{a_{k+1}} \\
\boldsymbol{n}_{w_{k+1}} \\
\boldsymbol{n}_{b_{a}} \\
\boldsymbol{n}_{b_{w}}
\end{array}\right]
Xk+1=⎣⎡δαk+1δθk+1δβk+1δbak+1δbωk+1⎦⎤Xk=⎣⎡δαkδθkδβkδbakδbωk⎦⎤Nk=⎣⎡naknwknak+1nwk+1nbanbw⎦⎤
结论:
δθk+1=[I−[ω‾]×δt]δθk+δt2nωk+δt2nωk+1−δtδbωk
\delta \boldsymbol{\theta}_{k+1}=\left[\boldsymbol{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t\right] \delta \boldsymbol{\theta}_{k}+\frac{\delta t}{2} \boldsymbol{n}_{\omega_{k}}+\frac{\delta t}{2} \boldsymbol{n}_{\omega_{k+1}}-\delta t \delta \boldsymbol{b}_{\omega_{k}}
δθk+1=[I−[ω]×δt]δθk+2δtnωk+2δtnωk+1−δtδbωk
δαk+1=δαk+δα˙kδt=δαk+δtδβk−δt24[Rk[ak−bak]×+Rk+1[ak+1−bak]×(I−[ω‾]×δt)]δθk−δt38Rk+1[ak+1−bak]×nωk−δt38Rk+1[ak+1−bak]×nωk+1+δt34Rk+1[ak+1−bak]×δbωk+δt24Rknak+δt24Rk+1nak+1−δt24(Rk+Rk+1)δbak \begin{aligned} \delta \boldsymbol{\alpha}_{k+1}= & \enspace \delta \boldsymbol{\alpha}_{k} + \delta \dot{\boldsymbol{\alpha}}_{k} \delta t \\ =& \enspace \delta \boldsymbol{\alpha}_{k} +\delta t \delta \boldsymbol{\beta}_{k} \\ &-\frac{\delta t^{2}}{4}\left[\boldsymbol{R}_{k}\left[\boldsymbol{a}_{k}-\boldsymbol{b}_{a_{k}}\right]_{\times}+\boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times}\left(\boldsymbol{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t\right)\right] \delta \boldsymbol{\theta}_{k} \\ &-\frac{\delta t^{3}}{8} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \boldsymbol{n}_{\omega_{k}} \\ &-\frac{\delta t^{3}}{8} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \boldsymbol{n}_{\omega_{k+1}} \\ &+\frac{\delta t^{3}}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \delta \boldsymbol{b}_{\omega_{k}} \\ &+\frac{\delta t^{2}}{4} \boldsymbol{R}_{k} \boldsymbol{n}_{a_{k}} \\ &+\frac{\delta t^{2}}{4} \boldsymbol{R}_{k+1} \boldsymbol{n}_{a_{k+1}} \\ &-\frac{\delta t^{2}}{4}\left(\boldsymbol{R}_{k}+\boldsymbol{R}_{k+1}\right) \delta \boldsymbol{b}_{a_{k}} \end{aligned} δαk+1==δαk+δα˙kδtδαk+δtδβk−4δt2[Rk[ak−bak]×+Rk+1[ak+1−bak]×(I−[ω]×δt)]δθk−8δt3Rk+1[ak+1−bak]×nωk−8δt3Rk+1[ak+1−bak]×nωk+1+4δt3Rk+1[ak+1−bak]×δbωk+4δt2Rknak+4δt2Rk+1nak+1−4δt2(Rk+Rk+1)δbak
δβk+1=δβk+δβ˙kδt=δβk−δt2[Rk[ak−bak]×+Rk+1[ak+1−bak]×(I−[ω‾]×δt)]δθk−δt24Rk+1[ak+1−bak]×nωk−δt24Rk+1[ak+1−bak]×nωk+1+δt22Rk+1[ak+1−bak]×δbωk+δt2Rknak+δt2Rk+1nak+1−δt2(Rk+Rk+1)δbak \begin{aligned} \delta \boldsymbol{\beta}_{k+1} = & \enspace \delta \boldsymbol{\beta}_{k} + \delta \dot{\boldsymbol{\beta}}_{k} \delta t \\ =& \enspace \delta \boldsymbol{\beta}_{k} \\ &-\frac{\delta t}{2}\left[\boldsymbol{R}_{k}\left[\boldsymbol{a}_{k}-\boldsymbol{b}_{a_{k}}\right]_{\times}+\boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times}\left(\boldsymbol{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t\right)\right] \delta \boldsymbol{\theta}_{k} \\ &-\frac{\delta t^{2}}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \boldsymbol{n}_{\omega_{k}} \\ &-\frac{\delta t^{2}}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \boldsymbol{n}_{\omega_{k+1}} \\ &+\frac{\delta t^{2}}{2} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \delta \boldsymbol{b}_{\omega_{k}} \\ &+\frac{\delta t}{2} \boldsymbol{R}_{k} \boldsymbol{n}_{a_{k}} \\ &+\frac{\delta t}{2} \boldsymbol{R}_{k+1} \boldsymbol{n}_{a_{k+1}} \\ &-\frac{\delta t}{2}\left(\boldsymbol{R}_{k}+\boldsymbol{R}_{k+1}\right) \delta \boldsymbol{b}_{a_{k}} \end{aligned} δβk+1==δβk+δβ˙kδtδβk−2δt[Rk[ak−bak]×+Rk+1[ak+1−bak]×(I−[ω]×δt)]δθk−4δt2Rk+1[ak+1−bak]×nωk−4δt2Rk+1[ak+1−bak]×nωk+1+2δt2Rk+1[ak+1−bak]×δbωk+2δtRknak+2δtRk+1nak+1−2δt(Rk+Rk+1)δbak
(9)F,G
Fk=[If12Iδt−14(Rk+Rk+1)δt2f150I−[ω‾]×δt00−Iδt0f32I−12(Rk+Rk+1)δtf35000I00000I] \mathbf{F}_{k}=\left[\begin{array}{ccccc} \mathbf{I} & \mathbf{f}_{12} & \mathbf{I} \delta t & -\frac{1}{4}\left(\boldsymbol{R}_{k}+\boldsymbol{R}_{k+1}\right) \delta t^{2} & \mathbf{f}_{15} \\ \mathbf{0} & \mathbf{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t & \mathbf{0} & \mathbf{0} & -\mathbf{I} \delta t \\ \mathbf{0} & \mathbf{f}_{32} & \mathbf{I} & -\frac{1}{2}\left(\boldsymbol{R}_{k}+\boldsymbol{R}_{k+1}\right) \delta t & \mathbf{f}_{35} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I} \end{array}\right] Fk=⎣⎡I0000f12I−[ω]×δtf3200Iδt0I00−41(Rk+Rk+1)δt20−21(Rk+Rk+1)δtI0f15−Iδtf350I⎦⎤
f12=−δt24[Rk[ak−bak]×+Rk+1[ak+1−bak]×(I−[ω‾]×δt)]f15=δt34Rk+1[ak+1−bak]×δbωkf32=−δt2[Rk[ak−bak]×+Rk+1[ak+1−bak]×(I−[ω‾]×δt)]f35=δt22Rk+1[ak+1−bak]× \begin{aligned} &\boldsymbol{f}_{12}=-\frac{\delta t^{2}}{4}\left[\boldsymbol{R}_{k}\left[\boldsymbol{a}_{k}-\boldsymbol{b}_{a_{k}}\right]_{\times}+\boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times}\left(\boldsymbol{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t\right)\right] \\ &\boldsymbol{f}_{15}=\frac{\delta t^{3}}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \delta \boldsymbol{b}_{\omega_{k}} \\ &\boldsymbol{f}_{32}=-\frac{\delta t}{2}\left[\boldsymbol{R}_{k}\left[\boldsymbol{a}_{k}-\boldsymbol{b}_{a_{k}}\right]_{\times}+\boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times}\left(\boldsymbol{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t\right)\right] \\ &\boldsymbol{f}_{35}=\frac{\delta t^{2}}{2} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \end{aligned} f12=−4δt2[Rk[ak−bak]×+Rk+1[ak+1−bak]×(I−[ω]×δt)]f15=4δt3Rk+1[ak+1−bak]×δbωkf32=−2δt[Rk[ak−bak]×+Rk+1[ak+1−bak]×(I−[ω]×δt)]f35=2δt2Rk+1[ak+1−bak]×
Gk=[14Rkδt2g1214Rk+1δt2g140amp;0012Iδt012Iδt0012Rkδtg3212Rk+1δtg34000000Iδt000000Iδt] \mathbf{G}_{k}=\left[\begin{array}{cccccc} \frac{1}{4} \boldsymbol{R}_{k} \delta t^{2} & \mathbf{g}_{12} & \frac{1}{4} \boldsymbol{R}_{k+1} \delta t^{2} & \mathbf{g}_{14} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \frac{1}{2} \mathbf{I} \delta t & \mathbf{0} & \frac{1}{2} \mathbf{I} \delta t & \mathbf{0} & \mathbf{0} \\ \frac{1}{2} \boldsymbol{R}_{k} \delta t & \mathbf{g}_{32} & \frac{1}{2} \boldsymbol{R}_{k+1} \delta t & \mathbf{g}_{34} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I} \delta t & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I} \delta t \end{array}\right] Gk=⎣⎡41Rkδt2021Rkδt00g1221Iδtg320041Rk+1δt2021Rk+1δt00g1421Iδtg3400000Iδt0amp;0000Iδt⎦⎤
g12=−δt38Rk+1[ak+1−bak]×g14=−δt38Rk+1[ak+1−bak]×g32=−δt24Rk+1[ak+1−bak]×g34=−δt24Rk+1[ak+1−bak]× \begin{aligned} &\boldsymbol{g}_{12}=-\frac{\delta t^{3}}{8} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \\ &\boldsymbol{g}_{14}=-\frac{\delta t^{3}}{8} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \\ &\boldsymbol{g}_{32}=-\frac{\delta t^{2}}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \\ &\boldsymbol{g}_{34}=-\frac{\delta t^{2}}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \end{aligned} g12=−8δt3Rk+1[ak+1−bak]×g14=−8δt3Rk+1[ak+1−bak]×g32=−4δt2Rk+1[ak+1−bak]×g34=−4δt2Rk+1[ak+1−bak]×
计算得到矩阵FkF_kFk和GkG_kGk后,即可按照上述公式来计算方差。
3.预积分残差关于待求状态量的雅可比
在优化时,需要求出残差对于求解的状态量的雅可比。
已知基于预积分量的状态更新如下:
[pwbjqwbjvjwbjabjg]=[pwbi+viwΔt−12gwΔt2+qwbiαbibjqwbiqbibjviw−gwΔt+qwbiβbibjbiabig]
\left[\begin{array}{c}
\mathbf{p}_{w b_{j}} \\
\mathbf{q}_{w b_{j}} \\
\mathbf{v}_{j}^{w} \\
\mathbf{b}_{j}^{a} \\
\mathbf{b}_{j}^{g}
\end{array}\right]=\left[\begin{array}{c}
\mathbf{p}_{w b_{i}}+\mathbf{v}_{i}^{w} \Delta t-\frac{1}{2} \mathbf{g}^{w} \Delta t^{2}+\mathbf{q}_{w b_{i}} \boldsymbol{\alpha}_{b_{i} b_{j}} \\
\mathbf{q}_{w b_{i}} \mathbf{q}_{b_{i} b_{j}} \\
\mathbf{v}_{i}^{w}-\mathbf{g}^{w} \Delta t+\mathbf{q}_{w b_{i}} \boldsymbol{\beta}_{b_{i} b_{j}} \\
\mathbf{b}_{i}^{a} \\
\mathbf{b}_{i}^{g}
\end{array}\right]
⎣⎡pwbjqwbjvjwbjabjg⎦⎤=⎣⎡pwbi+viwΔt−21gwΔt2+qwbiαbibjqwbiqbibjviw−gwΔt+qwbiβbibjbiabig⎦⎤
把上式左侧状态移到右侧,在理想的情况下左侧应该只剩下0,但是由于误差的存在,可以使用残差小量r代替,因此有:
[rprqrvrbarbg]=[pwbj−pwbi−viwΔt+12gwΔt2−qwbiαbibj2[qbibj∗⊗(qwbi∗⊗qwbj)]xyzvjw−viw+gwΔt−qwbiβbibjbja−biabjg−big]
\left[\begin{array}{c}
\mathbf{r}_{p} \\
\mathbf{r}_{q} \\
\mathbf{r}_{v} \\
\mathbf{r}_{b a} \\
\mathbf{r}_{b g}
\end{array}\right]=\left[\begin{array}{c}
\mathbf{p}_{w b_{j}}-\mathbf{p}_{w b_{i}}-\mathbf{v}_{i}^{w} \Delta t+\frac{1}{2} \mathbf{g}^{w} \Delta t^{2}-\mathbf{q}_{w b_{i}} \boldsymbol{\alpha}_{b_{i} b_{j}} \\
2\left[\mathbf{q}_{b_{i} b_{j}}^{*} \otimes\left(\mathbf{q}_{w b_{i}}^{*} \otimes \mathbf{q}_{w b_{j}}\right)\right]_{x y z} \\
\mathbf{v}_{j}^{w}-\mathbf{v}_{i}^{w}+\mathbf{g}^{w} \Delta t-\mathbf{q}_{w b_{i}} \boldsymbol{\beta}_{b_{i} b_{j}} \\
\mathbf{b}_{j}^{a}-\mathbf{b}_{i}^{a} \\
\mathbf{b}_{j}^{g}-\mathbf{b}_{i}^{g}
\end{array}\right]
⎣⎡rprqrvrbarbg⎦⎤=⎣⎡pwbj−pwbi−viwΔt+21gwΔt2−qwbiαbibj2[qbibj∗⊗(qwbi∗⊗qwbj)]xyzvjw−viw+gwΔt−qwbiβbibjbja−biabjg−big⎦⎤
更加复杂。。。。
练习2
样例代码给出使用LM算法估计曲线 y=e(ax2+bx+c)y = e^{(ax^2 + bx +c)}y=e(ax2+bx+c) 参数a,b,c 的完整过程。
(1)绘制样例代码中LM阻尼因子 μ\muμ 随迭代变化的曲线图。
运行代码,即可看到输出,将结果导入matlab即可绘制图象
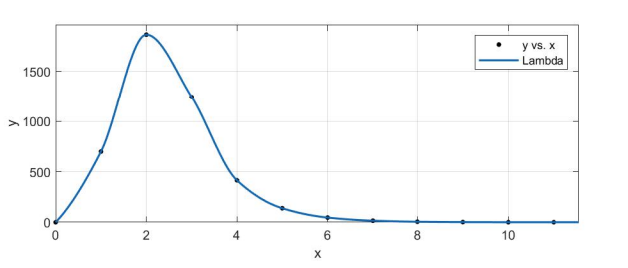
(2)将曲线函数改成 y=(ax2+bx+c)y = (ax^2 + bx +c)y=(ax2+bx+c) 修改代码
(3)其他阻尼因子更新策略





 本文围绕基于优化的IMU与视觉信息融合展开。首先介绍最小二乘问题求解,包括最速下降法、牛顿法等多种方法;接着阐述VIO残差函数构建,涉及系统状态量、重投影误差、IMU预积分等内容;还提及预积分残差关于待求状态量的雅可比。最后给出练习,如用LM算法估计曲线参数。
本文围绕基于优化的IMU与视觉信息融合展开。首先介绍最小二乘问题求解,包括最速下降法、牛顿法等多种方法;接着阐述VIO残差函数构建,涉及系统状态量、重投影误差、IMU预积分等内容;还提及预积分残差关于待求状态量的雅可比。最后给出练习,如用LM算法估计曲线参数。
















 1092
1092

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








