http://blog168.chinaunix.net/space.php?uid=20221192&do=blog&id=278899
一些网友写信给我希望能够了解固定流水线中世界空间到相机空间变换矩阵的具体推导过程。其实之前我在《向量几何在游戏编程中的使用6》中已经简单的把相机变换作为一个使用基理论的例子进行了说明,但可能仍然不够具体。这篇文章中,我会尽力阐述相机变换的整个来龙去脉。希望能够对正在学习固定流水线的朋友们有所帮助。这里我们仍然会在推导相机变换之前介绍几个理论知识,目的是为了更好的理解推导过程。我们马上开始!
什么是相机变换?在流水线中,当物体从模型坐标通过世界矩阵变换到世界空间之后,它将通过相机变换从世界空间变换到相机空间。下图的固定流水线中,蓝色框中的部分就是这个过程。
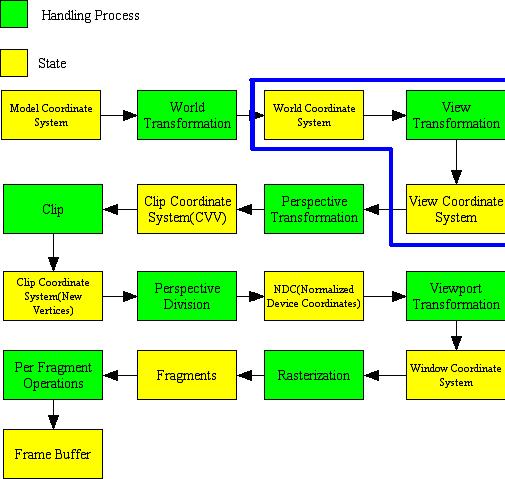
其实,所谓的相机空间,就是以相机作为坐标原点的一个参考系,所以,从世界空间变换到相机空间,就是把物体从世界坐标系,变换到相机为原点的相机坐标系,如下图所示。
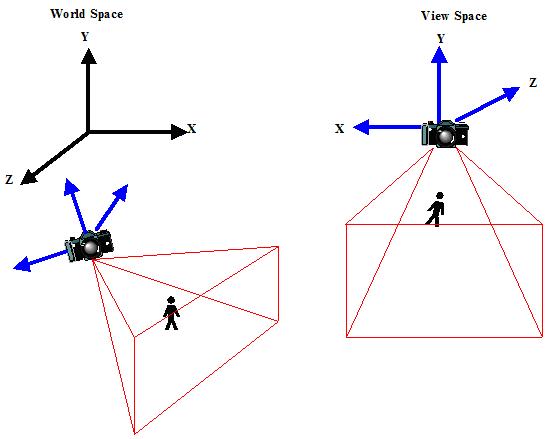
左半部分是小人在世界空间中的位置,右半部分是小人变换到相机空间后的位置。这样的一个变换可以有很多种方式来实现:欧拉相机系统、UVN系统、Two Points & A Twist等等。这里我们讨论最为广泛的UVN系统构建相机矩阵,如果读者对其他方法感兴趣,可以查找相关的资料。我们仍然讨论OpenGL的相机矩阵的推导,其他API可以类似的推导。
坐标转换公式我们在《向量几何在游戏编程中的使用6》中提到了正交矩阵,这是在基理论基础上的一个概念(如果对基理论不是很熟悉,请参考《向量几何在游戏编程中的使用6》)。正交矩阵所有列(行)向量构成了一个标准正交基(它的列向量都是互相正交,并且长度为1),因此,可以把正交矩阵看成是对一个坐标系的描述。同时,我们知道:同一个向量,在不同的基下面的坐标是不同的。因此,可以用正交矩阵来代表坐标系(也可以看作基)从而写出在统一的参考系(全局坐标系)下同一个向量在不同基中的坐标。
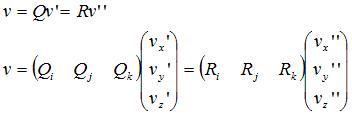
上面的式子表示,参考系中向量v在基Q中的坐标是v’,在基R中的坐标是v’’(注意这里的环境下基矩阵是用列向量表示的,这样相乘之后的结果表示的是基向量的线性组合)。如下图,黑色基表示的是参考系,红色是基Q,蓝色是基R,v是参考系中的一个向量。
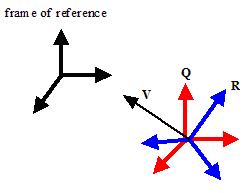
为了让大家更清楚,我举一个例子:
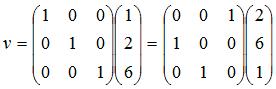
上式的意思是:参考系中的向量v,在基Q( 1 0 0 ), ( 0 1 0 ), ( 0 0 1)下的坐标是( 1 2 6 ),在基R( 0 1 0 ), ( 0 0 1 ), ( 1 0 0 )下的坐标是( 2 6 1 )。注意,我们所讨论的所有基和向量的关系都只是线性表示的关系,没有位移关系,因此我们用3D向量表示,而不是4D的齐次表示(如果对齐次坐标不是很熟悉,请参考《深入探索透视投影变换》中的齐次坐标部分)。
这样,已知一个基Q和向量v在它之中的坐标v’,以及另外一个基R,我们可以通过v=Qv’=Rv’’公式来计算v’’。
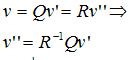
上面就是求v’’的公式,注意到右边需要计算基R的逆矩阵R^-1,因为基R是正交矩阵,而正交矩阵的一个重要性质就是逆等于转置。因此,我们可以把它写成
![]()
这个公式就是坐标转换公式。特别地,如果Q是和参考系相同的坐标系(3D编程中大多数情况下如此),比如世界坐标系,则Q是一个单位矩阵I,则我们可以把它写成
![]()
这个坐标转换公式可以解释为:对于世界坐标系中的向量v’,它在坐标系R中的坐标是v’’。我们在后面会用到这个公式。
除了用正交矩阵来阐述坐标转换,我们还可以使用点积所代表的共线程度(colinear amount)来描述坐标转换(André LaMothe的《Tricks Of The 3D Game Programming Gurus》)。这个理论基于点积的几何意义:一个向量在另一个向量上的共线程度。比如两个向量v和s点积
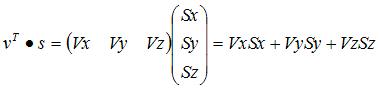
几何意义就是v在s方向上的投影长和s的长的乘积,或者是s在v方向上的投影长和v的长的乘积(积的符号为:若v和s的角度小于90度,积为正,如果是直角,积为零,否则为负)。
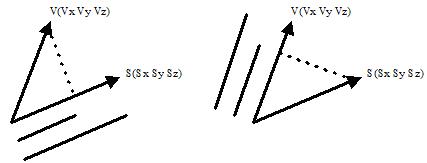
进一步地,如果v是一个单位向量,则这个点积可以解释为s在v方向上的投影长;如果s是一个单位向量,则可以解释为v在s方向上的投影长。现在,我们把点积推广到基的层次上,把一个向量v’和一个基R的三个单位轴向量进行点积,点积得到的三个值则表示这个向量在这个基下的坐标v’’
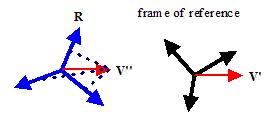
数学表达为
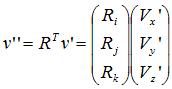
请注意,为了让v’能够和基的每一个轴向量进行点积,我们必须把基写成转置形式,即行向量乘法,否则就变成了线性组合的形式。这个公式的意义就是世界空间中的向量v’和基R的轴向量进行点积从而得到v’在R下的共线程度——坐标v’’。这个公式和上面我们得到的坐标转换公式一模一样。实际上我们是从两个不同的方向解释同一个公式,希望你能够把两个方向都理解。
UVN系统UVN系统本身是一个基。如下图所示,三个基向量U,V,N分别指向相机的右方、上方和后方从而构成右手坐标系,相机则处于坐标原点。
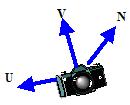
使用UVN系统可以非常方便的设置相机朝向。它的构建过程如下如所示
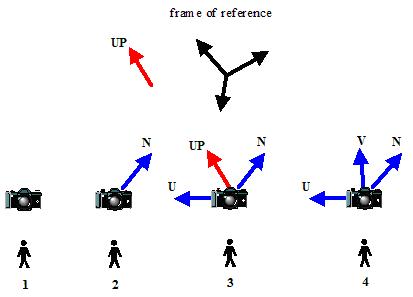
在参考系下(这里是世界坐标系),我们给定相机的位置——eye,被观察的小人的位置——lookat,以及一个辅助向量——参考系中表示“上方”的向量up,这个向量会影响U和V的生成,因为以后求出的V向量会在up和N向量所决定的平面上(有兴趣可以自己证明一下),所以可以通过这个向量让相机产生不同的偏转。

首先我们求出向量N
![]()
很简单,用目标位置减去相机的位置,就是图中的步骤2。第3步,我们求出向量U。这一步需要使用辅助向量up,如果不希望相机产生偏转,一般取(0, 1, 0)
![]()
U使用向量的叉乘实现,就是图中的步骤3。最后,使用N和U计算出向量V
![]()
最后将计算出的U,V和N进行单位化,就得到了相机的UVN系统。结合上面我们谈到的坐标转换理论,我们可以把UVN系统看作是相机的基,从而可以方便的把一个向量在世界坐标和相机坐标进行转换。
OpenGL的gluLookAt(eyex, eyey, eyez, lookatx, lookaty, lookatz, upx, upy, upz)方法就是使用的上面的步骤进行相机矩阵的设置。它的前三个参数就是相机的位置向量,中间三个参数是所观察的目标位置向量,最后三个参数就是辅助向量up。
相机矩阵的推导上面我们已经说明了UVN系统,标准流水线中就是使用了UVN系统来描述相机。U, V, N分别对应相机坐标系的三个基向量。
此外,对于一个相机来说,它在开始的时候和世界坐标系是重合的,用户控制相机在世界空间中移动之后,相机的状态可以用两个属性来描述——朝向和位置。也就是说,有了这两个属性,一个相机模型在世界中的状态就确定了。而这两个属性,我们用变换的理论来描述,就是旋转和平移。可以想象,对于世界中的任何一个相机状态,我们都可以把它看成是:相机先围绕自身基原点旋转一定的角度,然后平移到世界空间的某个地方。下图展示了这个过程
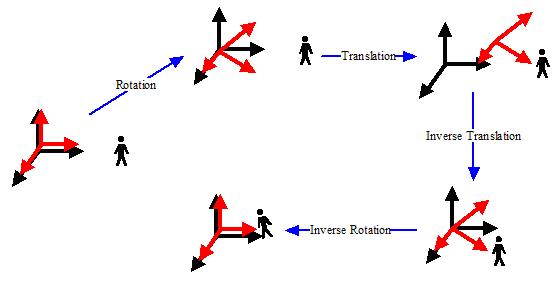
图中,红色是相机的基,而黑色是世界的基,也就是参考系。小人是世界中的一个物体。相机在移动之前,两个基是重合的。当相机在屏幕中定位时,它首先会进行朝向的确定——旋转,然后进行位置的确定——平移。图中的Rotation和Translation两步就是相机定位时所发生的变换。可以看到相机相对于小人的运动。而当进行相机变换的时候,小人应该从世界基变换到相机的基里面。这样,他应该进行一个相机定位的逆定位,先逆平移小人和相机,然后再逆旋转小人和相机,最后相机归位,小人随相机变到了相机空间。这是由Inverse Translation和Inverse Rotation两个步骤完成的,这两个步骤就是相机变换。现在我们推导这个变换。我们把关系写出来,相机本身的变换C包括两个元素
![]()
其中T是平移变换,R是旋转变换。而相机变换是相机本身变换的逆变换
![]()
这个C^-1就是我们要求出的相机变换。其中T^-1很容易求出,即
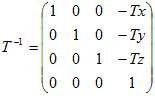
而R^-1就没有这么容易求出来了。所以,我们不求它,我们用UVN系统。什么意思?请看上面的那张相机变换的图,当相机变换进行完Inverse Translation这一步之后,相机的原点和世界原点就重合了,也就是处理完了关于平移的变换。接下来我们要做的是逆旋转,而其实逆旋转的目的,就是要得到目前世界坐标中经过逆平移的小人在相机坐标系中的坐标。是不是似曾相识?我们的坐标变换理论就派上用场了。我们回忆上面坐标变换的公式
![]()
这个坐标转换公式可以解释为:对于世界坐标系中的向量v’,它在坐标系R中的坐标是v’’。那么,我们可以套用在这里:对于世界坐标中的已经经过逆平移的坐标v’,它在相机坐标系R中的坐标是v’’。什么是相机坐标系R?就是我们的相机UVN系统!就是
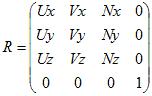
则相机变换的完整公式就是
![]()
这里,v是小人在世界空间中的坐标,v’’是小人在相机空间中的坐标。则相机变换矩阵就是
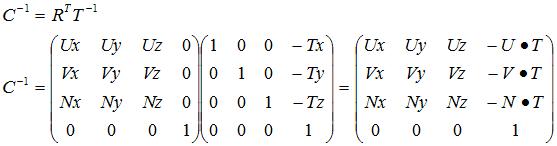
至此,我们就完成了相机矩阵的推导。物体经过这个矩阵就从世界空间变换到了相机空间,等待流水线对它进行投影变换。OpenGL就使用了上面推导出的最后的那个矩阵。希望你能够理解这个推导过程,如果你有什么问题或者不同的看法,请一定给我发信J下次见!





















 1096
1096

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








