马尔科夫决策过程之Bellman Equation（贝尔曼方程）

本文总结一下马尔科夫决策过程之Bellman Equation（贝尔曼方程）

 

1

Bellman Equation for MRPs

首先我们从value function的角度进行理解，value function可以分为两部分：

见下面的推导公式：

 

我们直接从第一行到最后一行是比较好理解的，因为从状态s到状态s+1,是不确定，还是之前的例子。

 

比如掷骰子游戏，当前点数是1的情况下，下一个状态有可能是1，2，3，4，5，6的任意一种状态可能，所以最外层会有一个期望符号。

 

如果我们跟着一直推下来的话：有疑问的会在导出最后一行时，将G(t+1)变成了v(St+1)。其理由是收获的期望等于收获的期望的期望。参考叶强童鞋的理解。

 

则最后我们得到了针对MRP的Bellman方程：

 

通过方程可以看出v(s)由两部分组成，一是该状态的即时奖励期望，即时奖励期望等于即时奖励，因为根据即时奖励的定义，它与下一个状态无关。

 

这里解释一下为什么会有期望符合，是因为从状态s的下一个状态s+1可能有多个状态，比如掷骰子，下一个状态可能有1，2，3，4，5，6，从s到下一个状态都是有一定概率，所以会有期望符合。

 

另一个是下一时刻状态的价值期望，可以根据下一时刻状态的概率分布得到其期望，比如在上面掷骰子例子中，从状态1到下一个状态1，2，3，4，5，6求期望的做法，我们可以直接用概率公式p(1->1),p(1->2),p(1->3),p(1->4),p(1->5),p(1->6) 然后乘以对应下一状态的价值函数即可。

 

如果用s’表示s状态下一时刻任一可能的状态，那么Bellman方程可以写成：

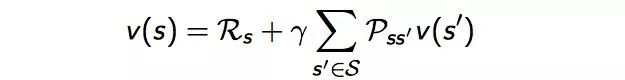
完整的slides如下：

 

 

2

Example: Bellman Equation for Student MRP

好，我们在上面既然知道了通过Bellman Equation来迭代的计算每个状态的价值函数，下面我们举出一个例子来算一个状态的value function帮助理解

 

 

通过上图我们分析一下4.3如何计算？见下图即可：

 

可能还有一些童鞋会问，算该状态的value function的时候，其它的状态的value function是怎么知道的呢？

 

比如算4.3的时候，我们如何知道它后继状态的value funciton为0.8，10。其实这些值一开始可以任意初始化，后面可以学习更新，就类似于神经网络的权值参数，一开始任意初始化，后面通过loss反向更新一样。

 

3

Bellman Equation in Matrix Form

最后我们可以给出Bellman方程的矩阵形式和求解

 

结合矩阵的具体表达形式如下：

 

 

总的slides如下：

 

 

Bellman方程是一个线性方程组，理论上解可以直接求解：

 

 

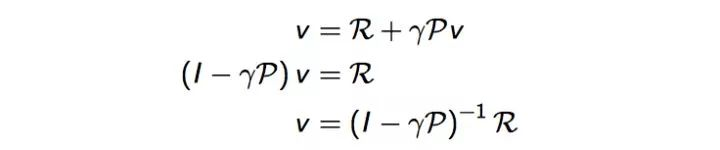
但是它的计算复杂度是0(n^3),  是状态数量,因为矩阵的求逆过程为0(n^3)。

由于求解复杂度较高。因此直接求解仅适用于小规模的MRPs。

 

大规模MRP的求解通常需要使用迭代法。常用的迭代方法有：

• 动态规划Dynamic Programming、
• 蒙特卡洛评估Monte-Carlo evaluation、
• 时序差分学习Temporal-Difference，