什么是白化

白化是将不同特征的相关性去掉相,并且将新特征的数据的的方差化为相同。
至于为什么需要白化,文中只说了有些算法需要它作为预处理,quora上的一个问题也许会有帮助。
https://www.quora.com/Computer-Vision-In-sphering-whitening-what-advantage-does-making-the-features-have-the-same-variance
如何白化
白化中第一步是使特性之间的相关性降低,这一步我们之前的PCA就已经做到了,回忆下pca的主要步骤
1. 计算矩阵的协方差矩阵(多个输入需要求平均)
2. 计算协方差矩阵的特征值和特征向量
3. 特征向量的装置左乘以原特征的数值得到新的特征的数值
4. 如果是想降维的话,特征值从大到小排列,选取一定信息量的特征值进行转换
5. 将降维后的新特征的值左乘特征向量,恢复到原始形式
这里第三步已经得到了不相关的特征的值,如果想要进一步白化,只需要将方差变为相同就好。
如何变为相同呢?
记得上一节(http://blog.csdn.net/bea_tree/article/details/51288570)我们提到过,协方差矩阵的对角阵就是方差,如果把每个数值都除以他的标准方差就可以使全部的数值的方差变为1了。这就是pca白化
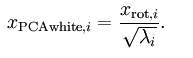
下图是服用前与服用后的变化,是不是水嫩白皙呢?
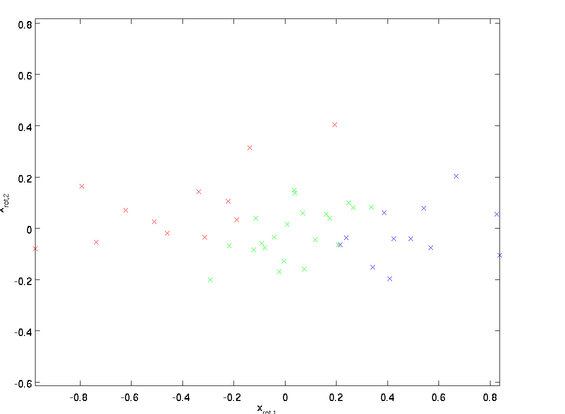
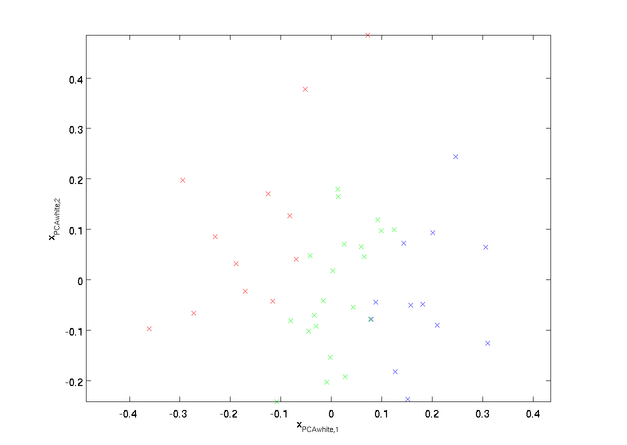
得到的新特征不相关且有着相同的方差,如果想既白化又降维,那就直接保留前k个特征就好了。
ZCA Whitening
ZCA白化就是在上面的pca白化的基础上将坐标系旋转下,转到原来的坐标系中,虽然数据不一样了,但是尽量去接近了原来的数值。(as close as possible to the original input data)
下面是公式和图片
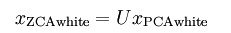
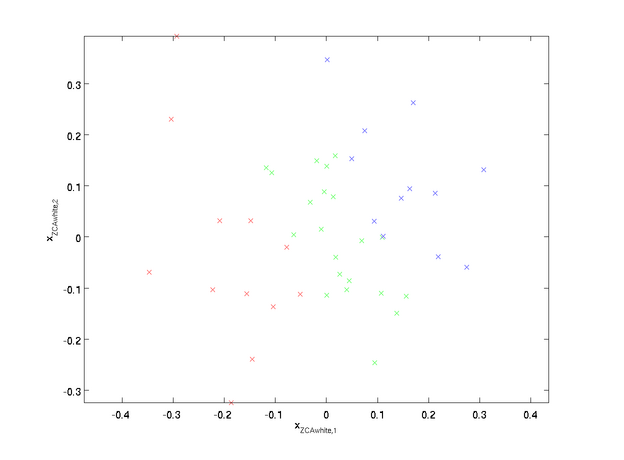
与pca不同的是,zca一般不再降维
zca的白化方式类似于人眼对图像的处理(this is done via retinal neurons that compute a function called “on center, off surround/off center, on surround”)。
Regularizaton 正则化
这里的正则化的作用是在进行pca白的时候,肯能会遇到原本发方差
λ
接近于0的情况,这时,如果直接除以它的根可能会出现不稳定的情况,因而一般将分母加入一个很小的数,一般在
10−5
左右如下式:

加入这个
ϵ
还会起到平滑数据的作用,改善学习性能。
























 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








