拉格朗日乘子法与KKT条件

拉格朗日乘子法与KKT条件

拉格朗日乘子法

在实际中我们常常遇到这样一种优化问题（min和max都是一样的，因为min f(x)等价于max -f(x)）：

$$\min f(x) \\ s.t \quad g(x)=0$$
这是一个等式约束问题，按照拉格朗日乘子法，可以转换为无条件约束的形式：
$$f(x)+\lambda g(x)=0$$
接下来分别对x和 $\lambda$求导即可：
$$\left\{\begin{matrix} \triangledown f(x)+\lambda \triangledown g(x)=0 \\ g(x)=0 \end{matrix}\right.$$
求解这个方程组即可。但是为什么可以这样做呢？
以这样一个问题为例：假设上面的x是一个二维的变量，即：
$$\min f(x_1, x_2) \\ s.t \quad g(x_1, x_2)=0$$

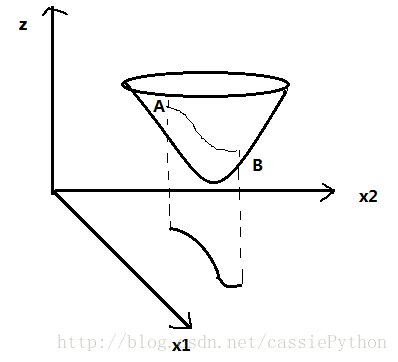
如图所示， $f(x_1, x_2)$ 是一个曲面， $g(x_1, x_2)=0$确定了一个曲线（若x是一个n维向量，则 $g(x_1, x_2)=0$ 确定了一个n-1维的曲面，因为n维向量和一个等式可得其中一个变量可由另外n-1个线性表示），我们的目的是在这条曲线上找一点能够使目标函数 $f(x_1, x_2)$ 取得最小值。为了便于观察，将这条曲线沿Z轴正向投影到曲面上，即我们沿着曲线从点A到点B找一点使曲面达到最低点。
现在还要补充一个预备知识，什么是等高线。假如我们有一个刀片，这个刀片平行于上图中的xOy面，我们不断的沿着Z轴移动这个刀片，它会与我们的曲面相交产生一系列的交线，我们把这些交线投影到xOy面上，于是得到下图（当然我们不可能画出所有的交线，只是部分）:

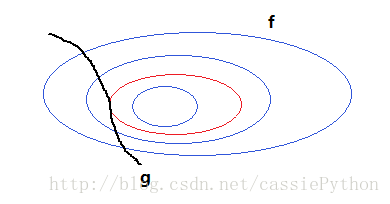
我们可以知道：

• 每一条圈上的函数值是相同的(用图一来说就是有相同的Z值)；
• 根据图一可以知道，圈越往里函数值越小；

• 圈与曲线相交的点对应着可取的点，该点所在的圈对应着可取的函数值
  
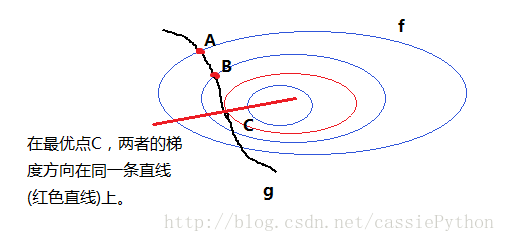
  下面说一下梯度，梯度表征了函数值变化最快的方向和速度，看上图在M点的梯度，沿着该梯度方向函数值减小最快，沿着它的逆方向函数值增大最快；曲面上任意一点，其等高线的切线方向与其梯度方向相互垂直；沿等高线的切线方向运动，函数值不变。此外我们有以下两个结论：

• 对于约束曲面(线)上的任意点x，该点的梯度$\triangledown g(x)$ 正交于约束曲面(线)

• 在最优点$x^*$ ，目标函数在该点的梯度$\triangledown f(x^*)$正交于约束曲面(线)
  
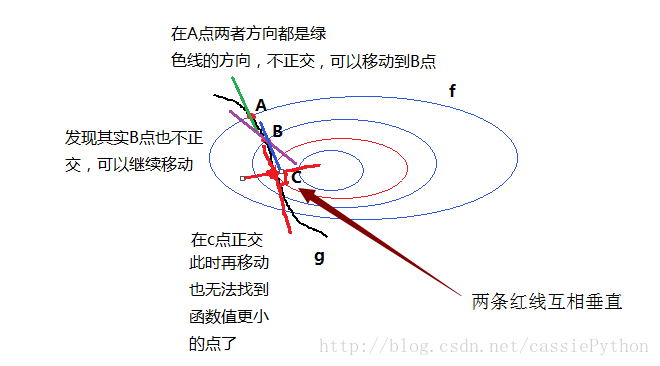
  第一点很明显，因为对于一个曲面(线)，它的法线的方向就是梯度的方向；关键是第二点，如上图假如最优点是A点，且目标函数在A点的梯度$\triangledown f(A)$ 与约束曲面不正交，我们看到存在一点B，其函数值f(B)比f(A)要小，这与我们的前提矛盾，也就是说若梯度$\triangledown f(x^*)$ 与约束平面不正交，则仍可在约束曲面上移动该点使函数值进一步下降（其实也可以根据两者的梯度来判断，往下看就明白这一点了）。
  
  于是我们得到最优点的位置如上图所示，在最优点$x^*$，梯度$\triangledown f(x)$ 与梯度$\triangledown g(x)$ 的方向必相同或相反，即存在$\lambda \neq 0$，使得：
  $$\triangledown f(x^*)+\lambda \triangledown g(x^*)=0$$
  而且$x^*$ 必定也是满足$g(x)=0$ 的，这正好对应了我们前面所说的拉格朗日的解决等式约束问题的方法，由此得证。
  

  KKT条件

现在我们可以解决等式约束的问题了，但是对于不等式约束如何处理呢？考虑下面的情况：

$$\min f(x) \\ s.t \quad h(x)=0 \\ \quad g(x)\leq 0$$
考虑 $g(x)\leq 0$，此时最优解 $x^*$ 或者在 $g(x)< 0$ 的区域中，或者在边界 $g(x)= 0$ 上，如下图所示：

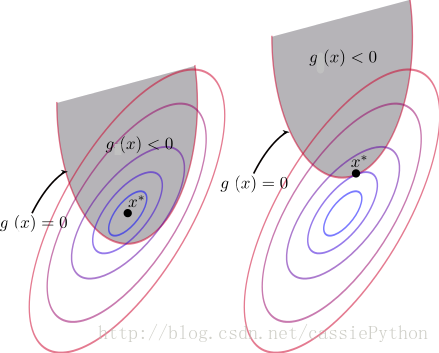
对上图左侧，此时最优解 $x^*$ 在 $g(x)< 0$ 的区域中；对上图右侧，最优解 $x^*$ 在边界 $g(x)= 0$ 上。对于左图的情况，即 $g(x)< 0$ 的情况，约束 $g(x)\leq 0$ 并没有起作用，比如你把左图的灰色区域去掉，是不是可以直接利用我们学过的方法得到最优解 $x^*$ ；对于右图的情况，很明显就是一个等式约束问题了，我们前面已经说过了，注意此时梯度 $\triangledown f(x)$ 与梯度 $\triangledown g(x)$ 的方向相反。由此原问题依然可以使用拉格朗日来解决，相应的拉格朗日函数为：
$$L(x,\lambda,\mu )=f(x)+\lambda h(x)+\mu g(x)$$
相应的KKT条件为：
$$\left\{\begin{matrix} g(x)\leq 0 \\ \mu\geq 0 \\ \mu g(x)=0 \end{matrix}\right.$$
当 $g(x)<0$时， $\mu=0$，原式中就不考虑g(x)；当 $g(x)=0$时， $\lambda$ 可取任何大于等于0的值。然后对于这样一个优化问题，我们可以使用拉格朗日对偶性将原问题转换为对偶问题，通过求对偶问题的解而得到原始问题的解。

---