以无刷直流电机为例,在矢量控制中,因为需要从转子角度对电机进行控制,所以需要对定子三相电流进行坐标变换,在旋转坐标系下对转矩和磁场进行解耦控制。控制输出需经过坐标反变换,在静止坐标系下生成电机驱动电路的控制信号。
1、Clarke变换和Park变换
将U、V、W三相电流转换为dq坐标系下的分量,其原理如图1中所示,即将静止坐标系下的IU、IV、IW在旋转的dq坐标轴上进行分解,合成新的d轴分量和q轴分量。
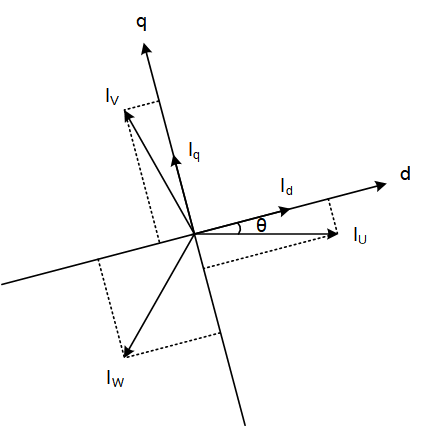
图1 dq变换原理示意
如图1中所示,dq旋转坐标系下电流分量的表达式为:
其中,θ为d轴和IU之间的角度,因为dq轴坐标系在不断旋转,所以θ随电机旋转而变化。
实际在MCU中实现坐标变换时,一般习惯性将上述分解过程分为两个步骤,即通常意义上的Clarke变换和Park变换。
1)Clarke变换
在Clarke变换中,首先将U、V、W相的电流变换为静止的αβ坐标系下的分量,如图2中所示。其中α轴和β轴正交,与dq坐标系不同,αβ坐标系为静止坐标系,α轴与U相同方向。αβ坐标系下的电流分量表达式为:

图2 Clarke变换
2)Park变换
接下来,再将αβ静止坐标分量变换为dq旋转坐标系下的分量,如图3中所示。d轴与磁体同方向,q轴与d轴垂直。dq坐标系下的电流分量表示为:
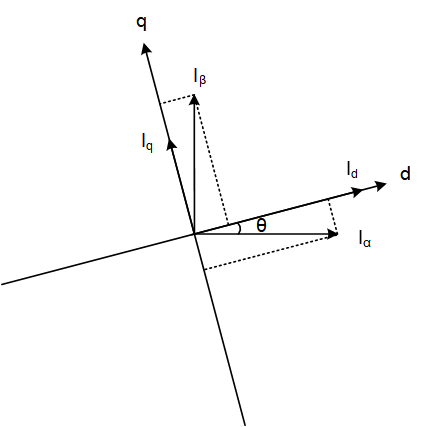
图3 Park变换
在Clarke变换和Park变换中,乘以2/3的目的在于保持变换前后电流的幅值保持不变,这种相对变换只是为了计算和理解的方便,从理论上不会影响闭环控制的结果。
2、Park逆变换和空间矢量变换
1)Park逆变换
Park逆变换用于将闭环控制(电流环)的结果(Vd和Vq)从dq旋转坐标系变换为αβ静止坐标系,计算公式为:
2)空间矢量变换
为了将Vα和Vβ转换为控制三相驱动电路的信号,需要对其进行空间矢量变换。其基本原理为:在一个PWM周期内,三相驱动电路中,上桥臂(u、v、w)和下桥臂(x、y、z)晶体管的开关组合有8中,除(000)和(111)之外,有6种电压矢量V1-V6对磁场的形成有贡献。所谓矢量控制,指的就是以这6种电压矢量为参考,构建包含6个区段的向量空间,根据Vα和Vβ的合成矢量V所在的区段,利用该区段的两个相邻矢量对V进行分解,得到在两个电压矢量上的分量。最后计算两个电压矢量的作用时间,生成三相驱动电路的控制信号波形。
以合成矢量V位于区段1时为例,变换过程如图4种所示。
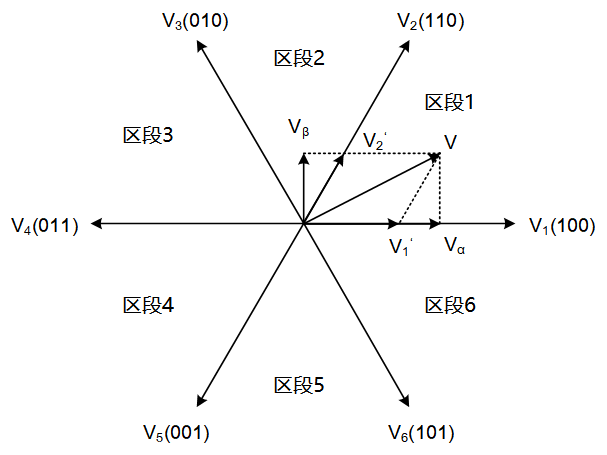
图4 空间矢量变换
根据图4可得:
根据PWM调制原理,若直流电压为VDC,PWM周期的一半为T,则
可以求得t1和t2,且
区段1的PWM波形如图5种所示。其中若V0和V7发生的时间分别为t3/2,则为三相调制;若V0发生的时间为t3,V7发生的时间为0,则为二相调制。

图5 区段1PWM波形
参考文献
[1]江崎雅康. 无刷直流电机矢量控制技术[M]. 北京: 科学出版社, 2019.

























 5177
5177

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










