图形几何学——圆形：圆弧与曲率

基于三个离散点求外接圆半径和曲率

方法1

A、B、C分别是参考线的某三个连续的离散点，abc分别是其对边。根据三角形外接圆相关性质，通过作三条边的中垂线的交点可以求得三角形的外接圆心。连接CO并延长交圆周于点D，由于

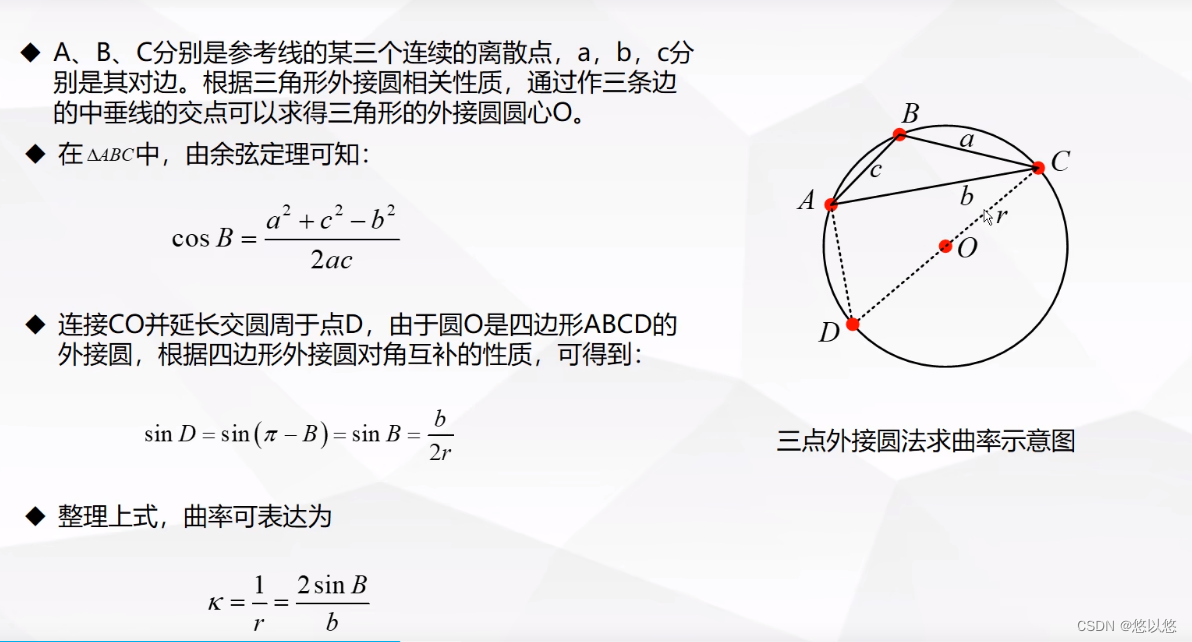
方法2

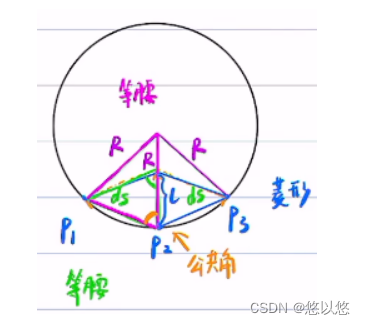
近似认为$|\overrightarrow{P_1}|=|\overrightarrow{P_2{P}_3}|=ds$相等，求向量$\overrightarrow{P_2{P}_1}$和向量$\overrightarrow{P_2{P}_3}$的向量和，记向量和的端点为$A$。易知四边形$D{P}_1{P}_2{P}_3$为菱形，$\Delta O{P}_1{P}_2$和$\Delta O{P}_2{P}_3$为等腰三角形，所以$\Delta O{P}_1{P}_2$和$\Delta P_1{P}_{2}D$相似，另外两个三角形同理，所以他们有以下关系
$$\frac{l}{ds}=\frac{ds}{R}$$
根据这个关系式可得
$$\kappa =\frac{1}{R}=\frac{l}{d{s}^2}$$
其中$l=|\overrightarrow{P_2{P}_1}+\overrightarrow{P_2{P}_3}|$

根据密切圆概念求轨迹的曲率

参考相关文献¹

• 曲率圆（密切圆）的定义
  如果我们要计算某一处的曲率，就在它的左右各取一个点，并用这三点确定一个圆。然后将左右两个点不断向中间靠拢，最终得到的圆，就是曲率圆。曲率圆就是对这个点附近曲线的最佳圆逼近。
• 曲率圆的特点
  • 曲线较为平坦的地方，曲率圆半径较大，较为弯曲的地方，曲率圆半径较小
• 根据曲率圆求曲率的过程
  假设一段曲线上取三个点，假设中间的点为$x_0$，左右两个点分别为$x_0-\delta$和$x_0+\delta$，由它们确定的圆的半径用$R$表示。

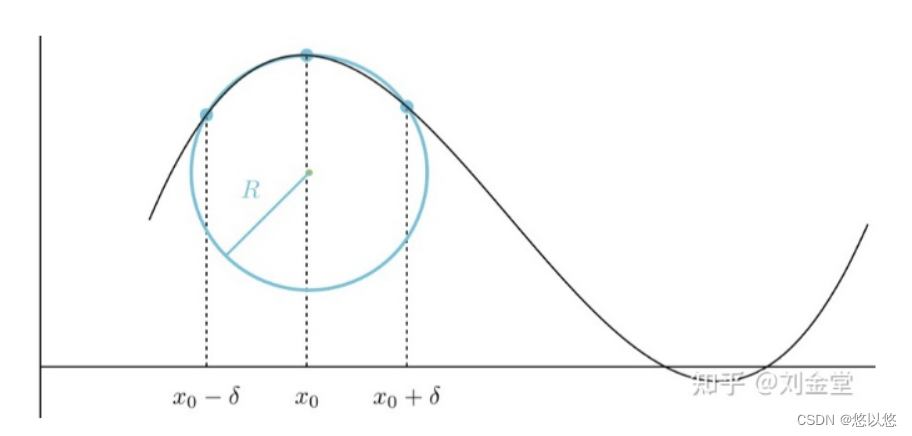
这个半径可以根据外接圆半径得到，$S_{\Delta ABC}$为这个三角形的面积，a,b,c为三个点构成三角形的三条边的边长，即三个向量的模，写作
$$\begin{array}{rl}R& =\frac{abc}{4S_{\Delta ABC}}\\ & =\frac{||a||\cdot ||b||\cdot ||c||}{4S_{\Delta ABC}}\end{array}$$

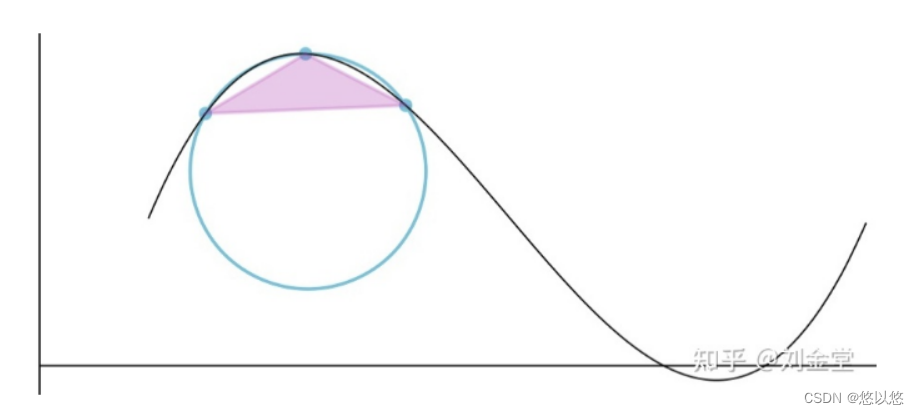
根据图形几何可知，向量a与向量b的点乘/行列式即为他们两所构成的平行四边形的面积，写作
$$S_{平行四边形}=2S_{\Delta ABC}=a\cdot b=\det (a,b)$$
即有
$$S_{\Delta ABC}=\frac{1}{2}|\det (a,b)|$$
将上式带回原式后可得
$$\begin{array}{rl}R& =\frac{||a||\cdot ||b||\cdot ||c||}{2|\det (a,b)|}\end{array}$$
设曲线函数为$f$，那么三个点的坐标为
$$\begin{gathered} (x_0-\delta ,f(x_0-\delta )) \\ (x_0,f(x_0)) \\ (x_0+\delta ,f(x_0+\delta )) \end{gathered}$$
那么三个向量分别写作
$$\begin{gathered} a=(\delta ,f(x_0+\delta )-f(x_0)) \\ b=(\delta ,f(x_0-f(x_0-\delta ))) \\ c=(-2\delta ,f(x_0+\delta )-f(x_0-\delta )) \end{gathered}$$
将上式代入，可得
$$R=\frac{\sqrt{[\frac{f(x_0+\delta )-f(x_0-\delta )}{\delta }{]}^2+4}\sqrt{[\frac{f(x_0+\delta )-f(x_0)}{\delta }{]}^2+1}\sqrt{[\frac{f(x_0+\delta )-f(x_0-\delta )}{\delta }{]}^2+1}}{2\left|\frac{f(x_0+\delta )+f(x_0-\delta )-2f(x_0)}{{\delta }^2}\right|}$$

让左右两边的点向中间靠，当$\delta \to 0$时，即可得到曲率圆的半径，写作
$$\begin{array}{rl}\underset{\delta \to 0}{\lim }R& =\frac{\sqrt{[\frac{f(x_0+\delta )-f(x_0-\delta )}{\delta }{]}^2+4}\sqrt{[\frac{f(x_0+\delta )-f(x_0)}{\delta }{]}^2+1}\sqrt{[\frac{f(x_0+\delta )-f(x_0-\delta )}{\delta }{]}^2+1}}{2\left|\frac{f(x_0+\delta )+f(x_0-\delta )-2f(x_0)}{{\delta }^2}\right|}\\ & =\frac{\sqrt{[\frac{f(x_0+\delta )-f(x_0-\delta )}{\delta }{]}^2+4}\sqrt{[\frac{f(x_0+\delta )-f(x_0)}{\delta }{]}^2+1}\sqrt{[\frac{f(x_0+\delta )-f(x_0-\delta )}{\delta }{]}^2+1}}{2\left|\frac{f(x_0+\delta )+f(x_0-\delta )-2f(x_0)}{{\delta }^2}\right|}\end{array}$$
综上，求路径半径及其曲率的公式为
$$R=\underset{\delta \to 0}{\lim }R=\frac{\{1+[f^{\prime }(x_0){]}^2{\}}^{\frac{3}{2}}}{|f^{\prime \prime }(x_0)|}$$
$$\kappa =\frac{1}{R}=\frac{|f^{\prime \prime }(x_0)|}{\{1+[f^{\prime }(x_0){]}^2{\}}^{\frac{3}{2}}}$$

---

1. 刘金堂的知乎专栏：https://zhuanlan.zhihu.com/p/590653546 ↩︎