目录
前言
第2节中,我们介绍了基于三点求外接圆的曲率,这种方法是一种最为精确的、基于数学原理的计算方法,接下来我们针对三个离散点建立二次曲线进行拟合的方式近似求解曲率,以拓展读者的数学思维。
一、基于三点参数方程的曲率计算方法



显然,为求解上式2参数曲线的曲率,必须首先计算式(1)的6个待定系数。记三个离散点构成的两段矢量的长度分别为:

考虑到A、B、C三个相邻离散点一般来说相隔很近,且对应的曲率半径的圆心角变化不大,则弧线段AB的长度可近似等于直线段AB的长度。因此,对于参数方程(1),自变量t的变化近似满足如下等式:

将式(4)代入(3),得到:
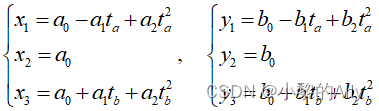
将上式改写为矩阵形式:
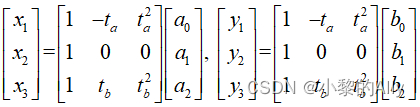
记:
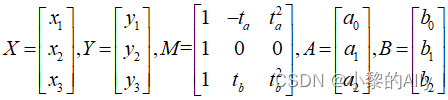
则求得待定系数矩阵为:

最后,将式(8)代入式(2),便可求得曲率。
二、实例介绍
1.MATLAB代码
我们同样利用圆形参考路径计算曲率,然后分别对比第2节和第3节的两种曲率计算方式。MATLAB代码如下:
clc
clear
close all
load refPath.mat
refPath = refPath_circle;
%% 基于三点求外接圆的曲率计算方法
for i = 1:size(refPath,1)-2
A = refPath(i,:);
B = refPath(i+1,:);
C = refPath(i+2,:);
a = norm(C-B);
b = norm(C-A);
c = norm(A-B);
theta_B = acos((a^2 + c^2 - b^2) / (2*a*c));
cur1(i) = 2*sin(theta_B) / b;
end
%% 基于三点参数方程的曲率计算方法
for i = 1:size(refPath,1)-2
x = refPath(i:i+2,1);
y = refPath(i:i+2,2);
ta = sqrt((x(2)-x(1))^2+(y(2)-y(1))^2);
tb = sqrt((x(3)-x(2))^2+(y(3)-y(2))^2);
M = [1,-ta,ta^2;
1,0,0;
1,tb,tb^2];
A = M\x;
B = M\y;
cur2(i) = abs(2*(A(2)*B(3)-A(3)*B(2)))/((A(2)^2+B(2)^2)^1.5+1e-10);
end
%% 计算路径长度
diff_x = diff(refPath(:,1)) ;
diff_y = diff(refPath(:,2)) ;
cumLength = cumsum(sqrt(diff_x.^2 + diff_y.^2));
%% 画图比较
% 图1:参考曲线
figure
grid on
plot(refPath(:,1), refPath(:,2),'LineWidth', 3, 'Color', 'b');
% 图2:两种曲率比较
figure
hold on
grid on
plot(cumLength(1:end-1), cur1,'LineWidth', 3, 'Color', 'b');
plot(cumLength(1:end-1), cur2,'r--','LineWidth', 3 );
% 图3:两种曲率差值
figure
hold on
grid on
% 主体图形绘制
plot(cumLength(1:end-1), cur1-cur2,'LineWidth', 3, 'Color', 'b');
2.结果分析
参考曲线路径是一个半径为20的圆,该圆由若干密集散点构成,如下图所示。

两种方法计算的曲率对比如下所示:其中蓝色实线代表第2节的方法,红色虚线为本节方法。
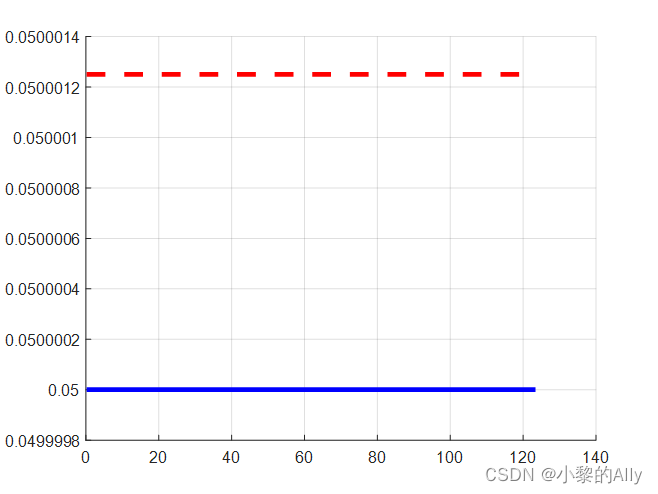
下图展示了两种方法计算曲率的差值对比,可以看出差值在1e-6的级别,基本可以忽略。

总结
因此,在对曲率不做较高精度要求时,第2节和第3节的两种方法可以通用。但也需要说明,方法三只是为读者提供了一种曲率计算的新颖思路,用于拓宽读者的数学思维,其计算过程和原理较方法二更为复杂,更推荐读者用方法二进行曲率计算。
本节部分参考资料:https://zhuanlan.zhihu.com/p/72083902h,对本思路方法的原创作者表示感谢,如有侵权,联系即删。

























 3235
3235

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










