
✅ 博主简介:擅长数据处理、建模仿真、程序设计、仿真代码、论文写作与指导,毕业论文、期刊论文经验交流。
✅ 具体问题可以私信或扫描文章底部二维码。
(1)启发式k-means算法的问题分析 传统的启发式k-means算法在初始簇中心的选择上完全随机,这可能导致算法陷入局部最优解。此外,算法需要人工设定参数k,即簇的数量,这对于非专家用户来说是一个挑战。同时,算法对于离群点非常敏感,容易受到异常值的影响,从而影响聚类结果的准确性。针对这些问题,本研究分析了启发式k-means算法的局限性,并提出了相应的改进措施。
(2)CHk-means算法的提出 CHk-means算法首先采用仔细播种方法来选择初始簇中心,以减少随机初始化带来的问题。这种方法通过评估数据点之间的距离,选择距离较远的点作为初始簇中心,从而提高了初始种群的质量。其次,算法采用肘方法来确定最优的k值。肘方法通过评估不同k值下的聚类误差,选择误差下降速率骤减的点作为最优k值。最后,CHk-means算法引入局部异常因子(LOF)算法来识别离群点,从而提高了聚类的鲁棒性。
(3)CHk-means算法的应用与评估 为了验证CHk-means算法的有效性,本研究在多个数据集上进行了实验。首先,对数据集进行了预处理,包括归一化和去除缺失值等步骤。然后,将CHk-means算法应用于这些数据集,并与其他聚类算法进行了比较。实验结果表明,CHk-means算法在降低聚类结果的误差平方和(SSE)和提高聚类的轮廓系数(SC)方面表现优异,聚类质量得到了显著改善。此外,本研究还将CHk-means算法应用于大规模的道路交通事故数据集,通过聚类结果成功识别出多个交通事故易发区域,并给出了各区域中心的经纬度坐标,为事故检测和应急处理提供了数据支持。与其他算法相比,CHk-means算法在误差平方和、轮廓系数、运行时间和聚类质量等指标上均展现出优越的性能。
% 初始化CHk-means算法的参数
k = 3; % 聚类数目
maxIterations = 100; % 最大迭代次数
% 运行CHk-means算法
[idx, centroids] = CHkmeans(dataset, k, maxIterations);
% 可视化聚类结果
figure;
hold on;
colors = lines(k);
for i = 1:k
clusterPoints = dataset(idx == i, :);
scatter(clusterPoints(:, 1), clusterPoints(:, 2), 10, colors(i, :), 'filled');
end
scatter(centroids(:, 1), centroids(:, 2), 100, 'k', 'filled');
title('CHk-means Clustering Results');
xlabel('Feature 1');
ylabel('Feature 2');
hold off;
% 定义CHk-means函数
function [idx, centroids] = CHkmeans(dataset, k, maxIterations)
% 初始化簇中心
centroids = initializeCentroids(dataset, k);
% 初始化簇标签
idx = assignDataPointsToClusters(dataset, centroids);
% 迭代更新簇中心和簇标签
for iter = 1:maxIterations
oldCentroids = centroids;
[idx, centroids] = assignDataPointsToClusters(dataset, centroids);
if isequal(oldCentroids, centroids)
break;
end
end
end
% 定义初始化簇中心的函数
function centroids = initializeCentroids(dataset, k)
% 使用仔细播种方法初始化簇中心
% ...
end
% 定义分配数据点到簇的函数
function [idx, centroids] = assignDataPointsToClusters(dataset, centroids)
% 分配数据点到最近的簇中心
% ...
end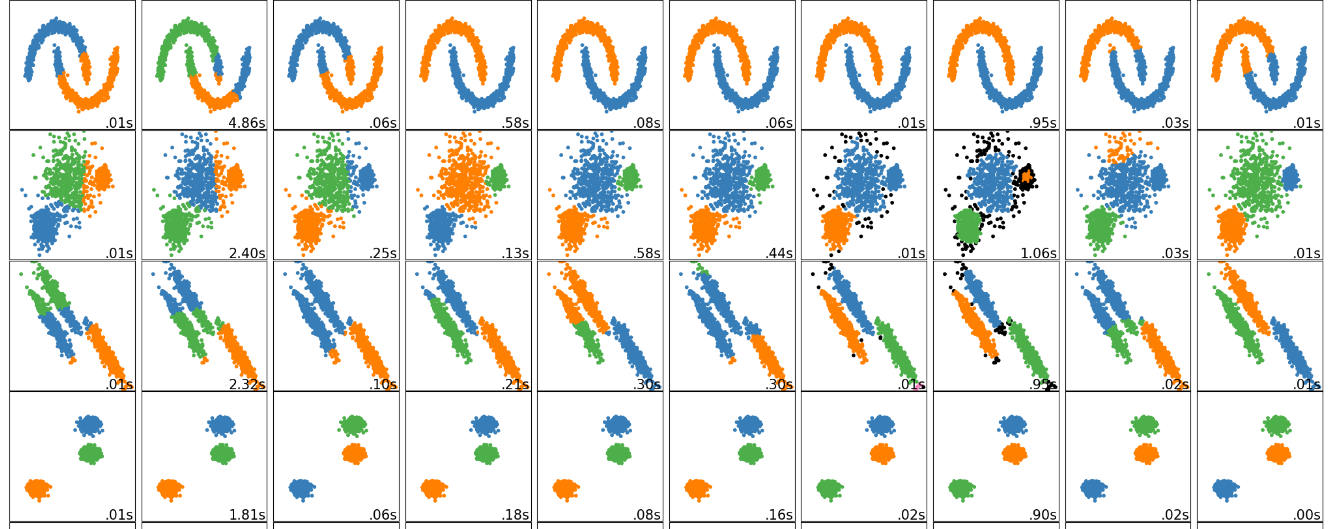
























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










