
✅ 博主简介:擅长数据搜集与处理、建模仿真、程序设计、仿真代码、论文写作与指导,毕业论文、期刊论文经验交流。
✅论文数据下载:工业工程毕业论文【数据集】
✅题目与创新点推荐:工业工业毕业论文【题目推荐】
(1)曲轴生产工序流程、作业时间和工作站划定及人员分配情况
D公司作为一家专注于为大型商用车生产发动机曲轴的企业,其生产线不仅承担着关键零部件的制造任务,同时也面临着如何在保证产品质量的前提下提升产能的重大挑战。为了更好地理解并优化这条混流生产线,首先需要对现有的生产工序进行详细的梳理和分析。从原材料准备到成品包装入库,整个过程涉及多个复杂环节,包括但不限于毛坯锻造、热处理、粗加工、精加工、检测以及最终装配等。
针对每一道工序,企业都制定了明确的标准作业时间,并根据实际需求合理划分了各个工作站。例如,在粗加工阶段,会将曲轴分为若干个主要部位分别进行车削、钻孔、铣削等工作;而到了精加工环节,则进一步细分为表面抛光、尺寸精度调整等具体操作。每个工作站都有固定的人员编制,确保有足够的劳动力来完成既定任务。此外,考虑到不同型号产品之间的差异性,部分工序还设置了专门的技术工人负责特殊工艺的执行,以保障各类产品的质量一致性。
然而,尽管有着较为完善的规划,但在实际运行过程中,仍不可避免地出现了一些问题,比如某些工位的工作量过于集中,导致员工长时间处于高强度劳动状态;或是由于设备故障或材料供应不足等原因造成停工待料现象频发。这些问题不仅影响了整体效率,也给企业的日常管理带来了不小的麻烦。因此,有必要借助先进的仿真软件工具如Flex Sim来进行更深入的研究,以便找到更加有效的解决方案。
(2)运用Flex Sim仿真软件建立曲轴生产线模型并分析
为了准确评估D公司曲轴生产线的实际表现,研究团队决定采用Flex Sim仿真软件构建一个虚拟环境下的生产线模型。该软件以其强大的图形化界面和灵活的参数设置功能著称,能够帮助用户直观地观察到整个生产流程中的每一个细节变化。通过导入真实工厂布局图、机床设备清单以及历史生产数据等信息,研究人员成功搭建起了一个与实物高度相似的数字孪生系统。
在这个模拟环境中,不仅可以实时监控每一台机器的工作状态,还能精确统计出所有参与生产的资源利用率,包括但不限于人力资源、物料流转速度、能源消耗水平等方面的数据。更重要的是,借助于内置的各种算法和统计工具,可以轻松计算出诸如生产线平衡率这样的关键性能指标。经过多次运行测试后发现,当前存在的主要问题集中在以下几个方面:
首先是产能不达标的问题。尽管按照理论计算应该能够满足市场需求,但实际产出却远远低于预期目标。其次是设备利用率偏低,尤其是那些高价值的专业加工中心,往往因为排程不合理或者维护保养不当而导致闲置时间过长。最后是生产线平衡率较低,这直接反映了各工作站点之间负载分配不均的事实,进而拖累了整体运作效率。
通过对上述问题的深入探讨,研究小组初步锁定了三个主要原因:存在瓶颈工序、设备布局不合理以及曲轴投产排序混乱。这些因素相互交织在一起,共同作用使得原本就紧张的生产条件变得更加棘手。接下来,就需要结合具体的工业工程方法和技术手段,逐一攻克难关,力求实现全方位的优化升级。
(3)5M1E分析法、基础工业工程方法及遗传算法的应用
面对复杂的曲轴生产线优化问题,研究团队采用了5M1E分析法作为切入点,即从人(Man)、机(Machine)、料(Material)、法(Method)、环(Environment)以及测量(Measurement)六个维度出发,全面剖析现有体系中存在的缺陷。这种方法强调综合考虑各种内外部影响因素,旨在找出最根本的原因所在。例如,在“人”的层面,重点关注员工技能水平是否匹配岗位要求,是否存在培训不足的情况;对于“机”,则仔细检查设备选型是否合适,保养计划是否科学合理;至于“料”,着重审查库存管理策略的有效性和供应链稳定性等等。
除了使用5M1E分析法外,研究还引入了一系列经典的基础工业工程方法和工具,如程序分析法、动作研究法、ECRS分析法等,针对之前识别出来的三大核心问题——瓶颈工序、设备布局不合理以及曲轴投产排序混乱——进行了针对性的设计改进。例如,在解决瓶颈工序的问题上,可以通过重新规划工艺路线,增加辅助设备或调整工序顺序等方式来分散压力;改善设备布局时,则要充分考虑到物流路径最短化原则,尽量减少不必要的搬运动作;而对于混乱的曲轴投产排序,则提出了基于遗传算法的多品种曲轴投产排序优化方案。
遗传算法是一种模仿自然界生物进化过程的人工智能搜索算法,它通过选择、交叉、变异等操作机制,在大规模解空间中快速寻找到接近最优解的答案。在本案例中,我们将这一算法应用于求解以混流投产的闲置和负荷成本最小化为目标的数学模型,期望能够在保证产品质量的同时降低运营成本。具体来说,就是利用MATLAB编写了一套定制化的遗传算法程序,经过反复迭代计算后得到了最佳的投产排序方案及其对应的闲置和负荷成本数值。
最后,为了验证所提出的优化措施是否有效,再次使用Flex Sim软件建立了优化后的曲轴生产线模型,并进行了详细的仿真分析。结果显示,经过一系列改造之后,整条生产线的表现有了显著提升:生产周期从原来的5923秒缩短至5460秒,生产节拍也由327秒优化到了280秒;与此同时,生产工序数从26道减少到23道,减少了3道工序,其中2道工序重排了加工顺序;生产线平衡率更是从62%提高到了85%,平均设备利用率也达到了81%,相比之前的55%有了明显进步。此外,日产量从最初的180支增长到了254支,JPH(Jobs Per Hour)也从9.0上升到了12.7支/小时;更重要的是,曲轴每日投产的闲置和负荷成本大幅下降,从40.1万元降至18.3万元,降幅达到54.36%,节省了21.8万元的成本支出。
不仅如此,优化后的生产线还带来了诸多附加价值,例如生产环境变得更加干净整洁,员工作业疲劳强度降低,工作满意度持续提高,从而使得企业综合竞争力得到全面提升。当然,任何一次变革都不可能是完美的,未来还需要不断探索和完善,特别是在智能制造技术的应用方面还有很大的发展空间。总之,这项研究表明,融合工业工程理论、智能算法和仿真技术等科学的优化方法,确实可以在很大程度上改善传统制造业的生产和管理水平。
% 以下是一个简化版的遗传算法示例代码,用于演示目的,并非真实D公司使用的完整代码。
% 实际应用中应根据具体情况进行定制开发。
% 注意:这里仅展示部分代码逻辑,完整实现需要更多的上下文信息和细节处理。
function [bestSolution, bestFitness] = optimize_production_schedule()
% 初始化参数
populationSize = 100; % 种群大小
numGenerations = 500; % 迭代次数
mutationRate = 0.01; % 变异概率
crossoverRate = 0.8; % 交叉概率
% 定义问题规模
numJobs = length(jobList); % jobList是从外部导入的任务列表
chromosomeLength = numJobs;
% 随机生成初始种群
population = randi([1, chromosomeLength], populationSize, chromosomeLength);
% 主循环开始
for generation = 1:numGenerations
% 计算适应度值
fitnessValues = zeros(populationSize, 1);
for i = 1:populationSize
fitnessValues(i) = calculate_fitness(population(i, :));
end
% 选择操作
parentsIndices = selection(fitnessValues, populationSize);
% 交叉操作
children = crossover(population(parentsIndices, :), crossoverRate);
% 变异操作
mutatedChildren = mutate(children, mutationRate);
% 更新种群
population = [population; mutatedChildren];
[~, idx] = sort(-fitnessValues);
population = population(idx(1:populationSize), :);
% 记录当前最好解
[bestFitness(generation), bestIdx] = max(fitnessValues);
bestSolution = population(bestIdx, :);
% 输出进度
if mod(generation, 50) == 0
fprintf('Generation %d: Best Fitness = %.2f\n', generation, bestFitness(generation));
end
end
% 辅助函数定义
function fitness = calculate_fitness(chromosome)
% 模拟计算适应度值,此处省略具体实现细节
fitness = sum(chromosome .* rand(size(chromosome))); % 示例计算方式
end
function indices = selection(fitnessValues, popSize)
% 选择操作,采用轮盘赌选择策略
probabilities = fitnessValues ./ sum(fitnessValues);
cumulativeProbabilities = cumsum(probabilities);
rands = rand(popSize, 1);
indices = arrayfun(@(x) find(cumulativeProbabilities >= x, 1, 'first'), rands);
end
function offspring = crossover(parents, rate)
% 单点交叉操作
numParents = size(parents, 1);
numOffspring = floor(numParents * rate);
offspring = zeros(numOffspring, size(parents, 2));
for i = 1:numOffspring
parentPair = datasample(parents, 2, 'Replace', false);
crossoverPoint = randi([1, chromosomeLength - 1]);
offspring(i, :) = [parentPair(1, 1:crossoverPoint), parentPair(2, crossoverPoint+1:end)];
end
end
function mutated = mutate(individuals, rate)
% 简单变异操作
numIndividuals = size(individuals, 1);
for i = 1:numIndividuals
for j = 1:chromosomeLength
if rand < rate
individuals(i, j) = randi([1, chromosomeLength]);
end
end
end
mutated = individuals;
end
end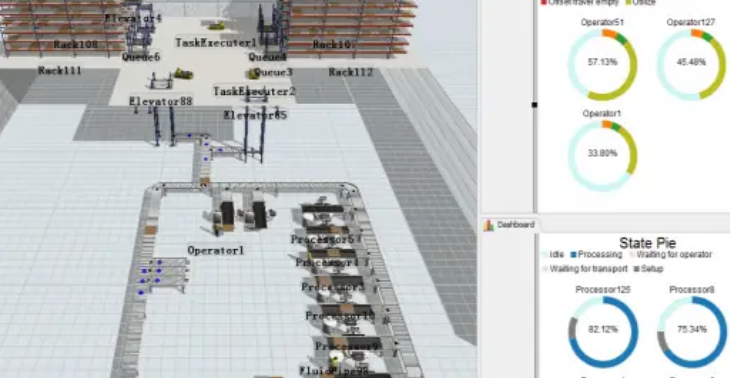
























 2879
2879

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










