合约对：IC2301&IC2302
价差计算
前-后（6082-6079.8）
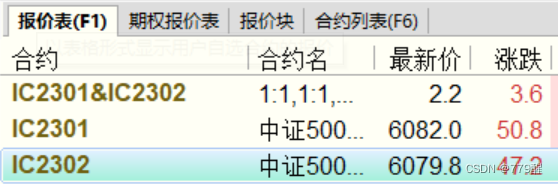
做多价差开仓（预期价差变大）
买2301（前）
卖2302（后）
做空价差开仓（预期价差变小）：
买2302（后）
卖2301（前）
二、交割时间
股指期货交割日为每月第三个周5，节假日顺延
棕榈油期货的交割月份为1-12月,最后交易日为交割月第十个交易日,最后交割日为最后交易日后第三个交易日
（例：P2301，最后交易日为1月13日，1月16日已无交易）
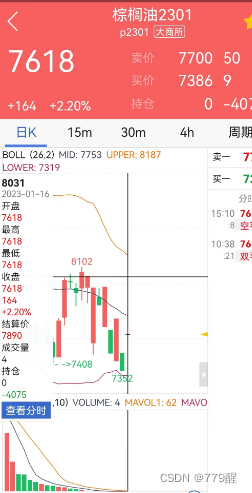
商品主力合约只产生在1月/5月/9月三个合约当中，例如1401，1405，1409会随着时间轮流的做为主力合约；
股指则是当月合约为主力合约。
三、软件选择
快期缺少前后腿操作，一年下来估计滑点也有万把块了。
尽量在默认合约里选，K线好像比较完整
四、观察现象解释
回测中的低点和极星软件中低点价差不同
9：30分前是集合竞价，回测程序中选取每天9：30之后的数据
2016年1月1日起,调整IF、IH、IC交易时间调整为集合竞价时间为每个交易日9:25-9:30,其中9:25-9:29为指令申报时间,9:29-9:30为指令撮合时间。连续竞价时间为每个交易日9:30-11:30为指令撮合时间。连续竞价时间为每个交易日9:30-11:30(第一节)和13:00-15:00(第二节)。”
当前课题：
商品期货套利观察
豆油和棕榈油
豆粕与和菜粕
玉米和玉米淀粉
螺纹钢和热卷
豆二和豆粕
2272
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
