NR 物理层编码 - slide 3 循环码Cyclic Code

最新推荐文章于 2023-10-12 15:18:30 发布

明朝百晓生

最新推荐文章于 2023-10-12 15:18:30 发布

阅读量1.7k

点赞数

分类专栏：芯片开发通讯技术文章标签： java 服务器 jvm

4AM_明朝百晓生

本文链接：https://blog.csdn.net/chengxf2/article/details/126847264

版权

芯片开发同时被 2 个专栏收录

94 篇文章 34 订阅

订阅专栏

通讯技术

54 篇文章 9 订阅

订阅专栏

参考

8.循环码-代数结构_哔哩哔哩_bilibili

循环移位算法 - rongyupan - 博客园

【信息论基础】第7章有噪信道编码—循环码_哔哩哔哩_bilibili

前言：

循环码是线性分组码的一种,应用比较广泛。一般写成（n,k)，输入k个bit,输出n个bit.

最常用的是CRC 算法.

核心是生成多项式,其主要性质如下

1 零次项为1

2 唯一性，不同信息经过编码后是唯一的

3 c(x) 的多项式都是g(x)的倍式

4 任何g(x)的倍式,若次数不超过n-1,一定在c(x)中

5 g(x)的次数等于校验位的个数(n-k)

6 g(x）是 $x^n+1$ 的一个因式（这个没有找到数学推导过程）

定义
码多项式
生成多项式g(x)
一致校验多项式 h(x)
系统结构的循环码
循环码例子
普通循环移位算法

一定义

循环码是线性分组码的一个重要子类

$\begin{Bmatrix} C \end{Bmatrix}$ 为线性分组码的码字集合,对任意码字 $c_i \in \begin{Bmatrix} C \end{Bmatrix}$ , $c_i$ 循环移位后得到的码字,

仍然属于该集合,则称该线性分组码为循环码

二码多项式

循环码主要通过码多项式表示和推导

$c=[c_{n-1},c_{n-2},...c_1,c_0]$

用码多项式表示为:

$c=c_{n-1}x^{n-1}+c_{n-2}x^{n-2}+...c_1 x^1+c_0$

例

码字 c= [1,0,1,1]

n=4

码多项式 $c(x)=x^{3}+x+1$

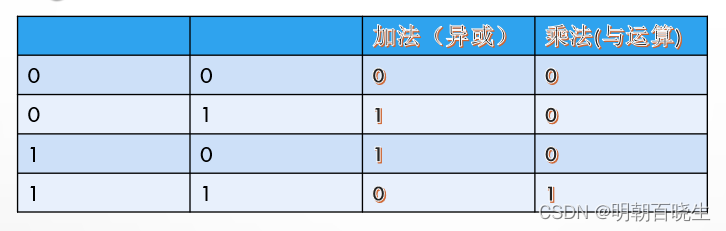
2.1 码多项式系数的 加乘运算

2.2 多项式中的同余类(余数相同,系统结构的循环码中运用到该概念）

$\frac{m(x)}{n(x)}=Q(x)+\frac{p(x)}{n(x)}$

$Q(x)$ 商| $p(x)$ 余数

$\frac{x^3+x+1}{x^2+x+1}= x+1+ p(x)$

$\frac{x^4+x^3+x^2+x}{x^2+x+1}= x^2+ p(x)$

余数都是 $p(x)=x$

商不同

2.3 定理1 多项式的模运算

$c^i(x)=[x^ic(x)]mod (x^n+1)$

若 c(x) 是长度为n的循环码中的一个码多项式,i 为不等于0的整数，

则 $x^ic(x)$ 模 $x^n+1$ 运算的余式为c(x)循环移动i位后的码字。

数学证明：

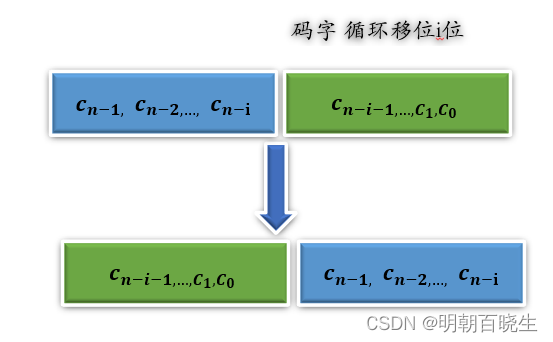
1: 码字循环移位i位的过程

原码字   $c=[c_{n-1},..c_{n-i},c_{n-i-1},...c_1,c_0]$

移位i位 $c=[c_{n-i-1},..c_0,c_{n-1},..c_{n-i}]$

移位后的码多项式为：

$c(x)=c_{n-1-i}x^{n-1}+...+c_1x^{i+1}+c_0x^{i}+c_{n-1}x^{i-1}+c_{n-2}x^{i-2}+...+c_{n-i}$

例如循环移动2位

第二步： $x^ic(x)$ 多项式形式

   $x^ic(x)=c_{n-1}x^{n-1+i}+c_{n-2}x^{n-2+i}+...+c_1x^{1+i}+c_0x^i$

每一项相当于   $c_jx^{j+i}$ $j\in[0,...n-1]$

第三步计算 $\frac{x^ic(x)}{x^{n+1}}$ 的模

只有 $c_{n-1}=1$ 时,才会对除数移位 $x^{i-1}$ ,所以等同于下面步骤



依次类推，最高到 $c_{n-i}x^{n-i+i}=c^{n-i}x^{n}$ 。

最后发现和第二步的码多项式是一样的。

以一个SPC循环码为例

举例

[101] $c(x)=x^2+1$ 左循环1位 ,对应 [011】码多项式为 $c(x)=x+1$

利用定理1,模运算取余数,实现的就是循环移位：

$\frac{x(x^2+1)}{x^3+1},p(x)=x+1$

[101] $c(x)=x^2+1$ 左循环2位, 对应[110] 码多项式 $c(x)=x^2+x$

$\frac{x^2(x^2+1)}{x^3+1},p(x)=x^2+x$

三生成多项式g(x)

3.1 定理2

根据定理1，选择合适的g(x)作为基准，通过 $x^ig(x)$ 就可以生成了循环码。

其基准可以通过码多项式来实现

在循环码(n,k)中,幂次数为r=n-k,且其常数项不等于0,的码字多项式

$g(x)=c_r x^r+c_{r-1}x^{r-1}+...c_1x+1$

$xg(x),x^2g(x),x^{k-1}g(x)$ 幂均小于n

g(x)称为生成多项式,是所有多项式的基准,这项的多项式有且只有1个。

码多项式矩阵

$G=\begin{bmatrix} x^{k-1}g(x)\\ x^{k-2} g(x) \\ ... \\ g(x) \end{bmatrix}$

定理： 循环码中所有的码多项式都可以被生成多项式整除，或是其倍式

证明：

$u=[a_{k-1},a_{k-2},...a_0]$

$c(x)=uG(X)=(a_{k-1}x^{k-1}+...a_0)g(x)$

所以循环码每个码字都是生成多项式的倍式

。

3.2 生成多项式充要条件

条件3到底怎么证明,没有搞懂。

条件2，其实就是唯一性，对于不同的输入信息，其生成的循环码应该是唯一的。

如果g(x)=0,则生成的循环码全是0，无法区分原信息。

生成多项式先对 $x^{n}+1$ 因式分解，然后找到满足前两项的因式

例：已知

$x^7+1=(x+1)(x^3+x+1)(x^3+x^2+1)$

求（7,3）循环码生成多项式

解：

r=7-3=4

$g(x)=\left\{\begin{matrix} (x+1)(x^3+x+1)\\ (x+1)(x^3+x^2+1) \end{matrix}\right.$

$=\left\{\begin{matrix} x^4+x^2+x+1\\ x^4+x^3+x^2+1 \end{matrix}\right.$

四一致校验多项式

因为 $x^n+1=g(x)h(x)$

h(x) 可以作为循环码一致校验多项式

根据 $c(x)=u(g)g(x)$

$h(x)c(x)=(x^n+1)u(x)$

例：

$x^7+1=(x+1)(x^3+x+1)(x^3+x^2+1)$

五系统码结构的循环码

系统码结构必须前面是信息元后面试监督元。

编码过程：

$x^{n-k}u(x)+p(x)$

其中：

$p(x)=x^{n-k}u(x)\begin{pmatrix} mod \end{pmatrix}g(x)$ ,最高幂次数为n-k-1

证明：

信息元

$u=[a_{k-1},..a_0]$ , $u(x)=a_{k-1}x^{k-1}+...+a_0$

编码后的系统码结构如下

系统码为 $A(x)+B(x)$

$A(x)=a_{k-1}x^{n-1}+a_{k-2}x^{n-2}+...a_0x^{n-k}$ $=x^{n-k}u(x)$

计算

$\frac{x^{n-k}u(x)}{g(x)}=Q(x)+\frac{p(x)}{g(x)}$ (p(x)为余数，最高幂为n-k-1,相当于监督元部分)

$x^{n-k}u(x)=Q(x)g(x)+p(x)$

$x^{n-k}u(x)+p(x)=Q(x)g(x)$

另一种理解方案就是编码后，c(x) mod g(x) 余数为0

$\frac{x^{n-k}u(x)+p(x)}{g(x)}=\frac{x^{n-k}u(x)}{g(x)}+\frac{p(x)}{g(x)}$

$=p(x)+p(x)=0$ (这里面除法代表取余运算）

例：已知（7,4）循环码生成多项式 $g(x)=x^3+x^2+1$

信息元 $u=[1100]$ ，分别求循环码,以及系统循环码

解：

$u(x)=x^3+x^2$

循环码

$c(x)=u(x)g(x)=x^6+x^4+x^3+x^2,c=[1011,100]$

系统循环码

$x^{n-k}u(x)=x^6+x^5$

$p(x)=\frac{x^6+x^5}{x^3+x^2+1}$ $=x^2+1$

$c(x)=x^6+x^5+x^2+1$ $=[1100,101]$

六循环码例子

3.1 循环码（7,4）生成多项式 $g(x)=x^3+x+1$

输入码字 $u=[1011],u(x)=x^3+x+1$

求输出码字：

解:

两种方案：

方案1

$c(x)=u(x)g(x)=(x^3+x+1)(x^3+x+1)$

$=x^6+x^4+x^3+x^4+x^2+x+x^3+x+1$

$=x^6+x^2+1$

$=[1000,101]$

方案2

3.2 生成多项式求法，一般物理层生成多项式是约定的,固定。

七循环移位算法

证明比较巧妙

# -*- coding: utf-8 -*-
"""
Created on Wed Sep 14 10:39:45 2022

@author: chengxf2
"""
import numpy as np

'''
翻转操作
'''
def reverse(bits):
    
    N = len(bits)
    start = 0
    end = N-1
    
    while(start<end):
        
        t= bits[start] #头尾
        bits[start]=bits[end]
        bits[end] = t
        
        start+=1
        end-=1
    #print(bits)
    return bits
    
'''
循环移位
k: 要移动的位数
bits  bit 流
'''    
def shift(k,bits,right):
    
     N = len(bits)
     
     k = k%N
     if k ==0:
         print("\n 保持",bits)
         return bits
     
     if right == True:
         left = bits[0:N-k]
         right = bits[N-k:]
     else:
         left = bits[0:k]
         right = bits[k:]
     
     left = reverse(left)
     print("\n 第一次翻转",left)
     
     right = reverse(right)
     print("\n 第二次翻转",right)
     left.extend(right)
     newBits = reverse(left)
     print("\n 第三次翻转后",newBits)
     
    

if __name__ =="__main__":
    
    bits =[1,2,3,4]
    shift(1,bits,False)