高斯混合模型的终极理解
<ul class="article_tags clearfix csdn-tracking-statistics tracking-click" data-mod="popu_377">
<li class="tit">标签:</li>
- 统计学 /
- GMM /
- EM算法 /
高斯混合模型GMM是一个非常基础并且应用很广的模型。对于它的透彻理解非常重要。网上的关于GMM的大多资料介绍都是大段公式,而且符号表述不太清楚,或者文笔非常生硬。本文尝试用通俗的语言全面介绍一下GMM,不足之处还望各位指正。
首先给出GMM的定义
这里引用李航老师《统计学习方法》上的定义,如下图:
定义很好理解,高斯混合模型是一种混合模型,混合的基本分布是高斯分布而已。
第一个细节:为什么系数之和为0?
PRML上给出过一张图:
这图显示了拥有三个高斯分量的一个维度的GMM是如何由其高斯分量叠加而成。这张图曾经一度对我理解GMM造成了困扰。因为如果是这样的话,那么这三个高斯分量的系数应该都是1,这样系数之和便为3,才会有这样直接叠加的效果。而这显然不符合GMM的定义。因此,这张图只是在形式上展现了GMM的生成原理而并不精确。
那么,为什么GMM的各个高斯分量的系数之和必须为1呢?
其实答案很简单,我们所谓的GMM的定义本质上是一个概率密度函数。而概率密度函数在其作用域内的积分之和必然为1。GMM整体的概率密度函数是由若干个高斯分量的概率密度函数线性叠加而成的,而每一个高斯分量的概率密度函数的积分必然也是1,所以,要想GMM整体的概率密度积分为1,就必须对每一个高斯分量赋予一个其值不大于1的权重,并且权重之和为1。
第二个细节:求解GMM参数为什么需要用EM算法
总所周知,求解GMM参数使用EM算法。但是为什么呢?这样是必须的吗?
首先,类似于其他的模型求解,我们先使用最大似然估计来尝试求解GMM的参数。如下:
可以看出目标函数是和的对数,很难展开,优化问题麻烦,难以对其进行求偏导处理。因此只能寻求其它方法。那就是EM算法。
第三个细节:求解GMM的EM算法隐变量的理解
使用EM算法必须明确隐变量。求解GMM的时候设想观测数据x是这样产生的:首选依赖GMM的某个高斯分量的系数概率(因为系数取值在0~1之间,因此可以看做是一个概率取值)选择到这个高斯分量,然后根据这个被选择的高斯分量生成观测数据。然后隐变量就是某个高斯分量是否被选中:选中就为1,否则为0。
按照这样的设想:隐变量是一个向量,并且这个向量中只有一个元素取值为1,其它的都是0。因为假设只有一个高斯分量被选中并产生观测数据。然而我们的GMM的一个观测数据在直观上应该是每个高斯分量都有产生,而不是由一个高斯分量单独生成,只是重要性不同(由系数控制)。那么,这样的隐变量假设合理吗?
答案是合理,只是理解起来比较“费劲”而已。
首先明确一点:GMM的观测数据是啥,GMM的函数结果又是啥。如果是一个一维的GMM,那么其观测数据就是任意一个实数。而GMM这个概率密度函数在输入这个观测数据之后输出的是这个实数被GMM产生的概率而已。
接着,现在我们不知道GMM具体的参数值,想要根据观测数据去求解其参数。而GMM的参数是由各个高斯分量的参数再加上权值系数组成的。那么我们就先假定,如果这个观测值只是由其中一个高斯分量产生,去求解其中一个高斯分量的参数。我们假设不同的观测值都有一个产生自己的唯一归宿,就像K-means算法一样。然后在后面的迭代过程中,根据数据整体似然函数的优化过程,逐渐找到一个最优的分配方案。然而,不同于K-means算法的是,我们最终给出的只是某一个观测是由某一个高斯分量唯一生成的概率值,而不是确定下来的属于某一类。每个高斯分量其实都可以产生这个观测数据只是输出不同而已,即产生观测数据的概率不同。最后,根据每个高斯分量产生观测数据的可能性不同,结合其权值汇总出整个GMM产生这个观测数据的概率值。
终极理解:使用EM算法求解GMM参数
1、定义隐变量
我们引入隐变量γjk,它的取值只能是1或者0。
- 取值为1:第j个高斯分量
- 取值为0:第j个高斯分量
那么对于每一个观测数据yj,那么有:
∑k=1Kγjk=1
p(Γj)=∏k=1Kαkγjk
其中, K的先验分布概率。2、得到完全数据的似然函数
对于观测数据yj,当已知其是哪个高斯分量生成的之后,其服从的概率分布为:
p(yj|γjk=1;Θ)=N(yj|μk,Σk)p(y_j|\gamma_{jk}=1;\Theta)={N(y_j|\mu_k,\Sigma_k)}
由于观测数据从哪个高斯分量生成这个事件之间的相互独立的,因此可以写为:
p(yj|Γj;Θ)=∏k=1KN(yj|μk,Σk)γjkp(y_j|\Gamma_j;\Theta)=\prod_{k=1}^K{N(y_j|\mu_k,\Sigma_k)}^{\gamma_{jk}}
这样我们就得到了已知 Γj的先验分布,则我们可以写出单个完全观测数据的似然函数为:
p(yj,Γj;Θ)=∏k=1KαkγjkN(yj|μk,Σk)γjkp(y_j,\Gamma_j;\Theta)=\prod_{k=1}^K{\alpha_k}^{\gamma_{jk}}{N(y_j|\mu_k,\Sigma_k)}^{\gamma_{jk}}
最终得到所有观测数据的完全数据似然函数为:
p(y,Γj;Θ)=∏j=1N∏k=1KαkγjkN(yj|μk,Σk)γjkp(y,\Gamma_j;\Theta)=\prod_{j=1}^N\prod_{k=1}^K{\alpha_k}^{\gamma_{jk}}{N(y_j|\mu_k,\Sigma_k)}^{\gamma_{jk}}
取对数,得到对数似然函数为:
lnp(y,Γj;Θ)=∑j=1N∑k=1K(γjklnαk+γjklnN(yj|μk,Σk))lnp(y,\Gamma_j;\Theta)=\sum_{j=1}^N\sum_{k=1}^K({{\gamma_{jk}}ln\alpha_k}+{\gamma_{jk}}ln{N(y_j|\mu_k,\Sigma_k)})3、得到各个高斯分量的参数计算公式
首先,我们将上式中的lnN(yj|μk,Σk)根据单高斯的向量形式的概率密度函数的表达形式展开:
lnN(yj|μk,Σk)=−D2ln(2π)−12ln|Σk|−12(yj−μk)TΣ−1k(yj−μk)ln{N(y_j|\mu_k,\Sigma_k)}=-\frac{D}{2}ln(2\pi)-\frac{1}{2}ln|\Sigma_k|-\frac{1}{2}(y_j-\mu_k)^T\Sigma_k^{-1}(y_j-\mu_k)假设我们已经知道隐变量γjk求偏导并且偏导结果为零,可以得到:
μk=∑Nj=1∑Kk=1γjkyj∑Nj=1∑Kk=1γjk\mu_k=\frac{\sum_{j=1}^N\sum_{k=1}^K\gamma_{jk}y_j}{\sum_{j=1}^N\sum_{k=1}^K\gamma_{jk}}
Σk=∑Nj=1∑Kk=1γjk(yj−μk)(yj−μk)T∑Nj=1∑Kk=1γjk\Sigma_k=\frac{\sum_{j=1}^N\sum_{k=1}^K\gamma_{jk}(y_j-\mu_k)(y_j-\mu_k)^T}{\sum_{j=1}^N\sum_{k=1}^K\gamma_{jk}}
由于在上面两式的第二个求和符号是对 k=1…K只有以此取到1,其它都是0,因此上面两式可以简化为:
μk=∑Nj=1γjkyj∑Nj=1γjk\mu_k=\frac{\sum_{j=1}^N\gamma_{jk}y_j}{\sum_{j=1}^N\gamma_{jk}}
Σk=∑Nj=1γjk(yj−μk)(yj−μk)T∑Nj=1γjk\Sigma_k=\frac{\sum_{j=1}^N\gamma_{jk}(y_j-\mu_k)(y_j-\mu_k)^T}{\sum_{j=1}^N\gamma_{jk}}
现在参数空间中剩下一个 αk求偏导,可以得到:
αk=∑Nj=1γjk−λ\alpha_k=\frac{\sum_{j=1}^N\gamma_{jk}}{-\lambda}
将上式的左右两边分别对 k=1…K求和,可以得到:
λ=−N\lambda=-N
将 λ代入,最终得到:
αk=∑Nj=1γjkN\alpha_k=\frac{\sum_{j=1}^N\gamma_{jk}}{N}
至此,我们在隐变量已知的情况下得到了GMM的三种类型参数的求解公式。4、得到隐变量的估计公式
根据EM算法,现在我们需要通过当前参数的取值得到隐变量的估计公式也就是说隐变量的期望的表达形式。即如何求解E{γjk|y,Θ}。
E{γjk|y,Θ}=P(γjk=1|y,Θ)E\{\gamma_{jk}|y,\Theta\}=P(\gamma_{jk}=1|y,\Theta)
=P(γjk=1,yj|Θ)∑Kk=1P(γjk=1,yj|Θ)=\frac{P(\gamma_{jk}=1,y_j|\Theta)}{\sum_{k=1}^KP(\gamma_{jk}=1,y_j|\Theta)}
=P(yj|γjk=1,Θ)P(γjk=1|Θ)∑Kk=1P(yj|γjk=1,Θ)P(γjk=1|Θ)=\frac{P(y_j|\gamma_{jk}=1,\Theta)P(\gamma_{jk}=1|\Theta)}{\sum_{k=1}^KP(y_j|\gamma_{jk}=1,\Theta)P(\gamma_{jk}=1|\Theta)}
=αkN(yj|μk,Σk)∑Kk=1αkN(yj|μk,Σk)=\frac{\alpha_kN(y_j|\mu_k,\Sigma_k)}{\sum_{k=1}^K\alpha_kN(y_j|\mu_k,\Sigma_k)}5、使用EM算法迭代进行参数求解
熟悉EM算法的朋友应该已经可以从上面的推导中找到EM算法的E步和M步。GMM和K-means直观对比
最后我们比较GMM和K-means两个算法的步骤。
GMM:
- 先计算所有数据对每个分模型的响应度
- 根据响应度计算每个分模型的参数
- 迭代
K-means:
- 先计算所有数据对于K个点的距离,取距离最近的点作为自己所属于的类
- 根据上一步的类别划分更新点的位置(点的位置就可以看做是模型参数)
- 迭代
可以看出GMM和K-means还是有很大的相同点的。GMM中数据对高斯分量的响应度就相当于K-means中的距离计算,GMM中的根据响应度计算高斯分量参数就相当于K-means中计算分类点的位置。然后它们都通过不断迭代达到最优。不同的是:GMM模型给出的是每一个观测点由哪个高斯分量生成的概率,而K-means直接给出一个观测点属于哪一类。











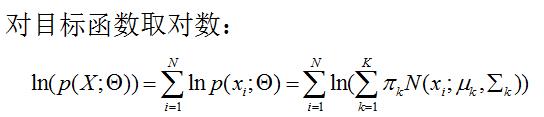














 10万+
10万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








