能量不等式的证明

波动方程初值问题能量不等式的证明

Gronwall 不等式

若非负函数 $G(\tau )$ 在$[0,T]$ 上连续可微，$G(0)=0$，且对 $\tau \in [0,T]$满足 $$\frac{dG(\tau )}{d\tau }\le CG(\tau )+F(\tau )$$ 其中 $C$ 为常数且 $C>0$，$F(\tau )$ 是$[0,T]$ 上不减的非负可积函数，

那么有：

$$\frac{dG(\tau )}{d\tau }\le e^{C\tau }F(\tau )$$ $$G(\tau )\le C^{-1}(e^{C\tau }-1)F(\tau )$$

常用的替换技巧

$$u_t{u}_{tt}=\frac{1}{2}\cdot 2u_t\cdot u_{tt}=\frac{1}{2}(u_t^2{)}_t$$$$u{u}_t=\frac{1}{2}\cdot 2u\cdot u_t=\frac{1}{2}(u^2{)}_t$$$$u{u}_{xx}=(u{u}_x{)}_x-u_x^2=u_x^2+u{u}_{xx}-u_x^2$$$$\because (u_t{u}_x{)}_x=u_{tx}{u}_x+u_t{u}_{xx}$$$$\therefore u_t{u}_{xx}=(u_t{u}_x{)}_x-u_{tx}{u}_x$$

$u$ 二阶导函数连续时，$$u_{xt}=u_{tx}$$$$\therefore u_{tx}{u}_x=\frac{1}{2}(u_x^2{)}_t=\frac{1}{2}\cdot 2u_x\cdot u_{xt}=u_x{u}_{tx}$$$$\therefore u_t{u}_{xx}=(u_t{u}_x{)}_x-\frac{1}{2}(u_x^2{)}_t$$

能量不等式证明过程

规定 $x$ 增长的方向为正方向，而 $Green$ 公式曲线积分时，组成梯形区域 $K_{\tau }$ 边界 $\partial K_{\tau }$ 的四条线段按照右手法则，只有 ${\Omega }_0$ 这条线段的方向是与右手法则一致，所以有：

$\partial K_{\tau }={\Omega }_0\cup (-{\Gamma }_{{\tau }_2})\cup (-{\Omega }_{\tau })\cup (-{\Gamma }_{{\tau }_1})$

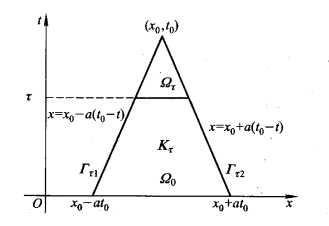
此外，在 $\partial K_{\tau }$ 计算曲线积分时，关于 $x,t$ 都积分，但是这两条边 ${\Omega }_0,{\Omega }_{\tau }$ 只在 $x$ 方向有增长，而在 $t$ 方向无增长，那么这两条线段在计算曲线积分时关于 $dt$ 的积分项为 $0$

待证明的两个不等式：
$${\int }_{{\Omega }_{\tau }}\left[u_t^2(x,\tau )+a^2{u}_x^2(x,\tau )\right]dx\le M\left[{\int }_{{\Omega }_0}({\psi }^2+a^2{\phi }_x^2)dx+{\iint }_{K_{\tau }}{f}^2(x,t)dxdt\right]$$$${\iint }_{K_{\tau }}\left[u_t^2(x,t)+a^2{u}_x^2(x,t)\right]dxdt\le M\left[{\int }_{{\Omega }_0}({\psi }^2+a^2{\phi }_x^2)dx+{\iint }_{K_{\tau }}{f}^2(x,t)dxdt\right]$$

1. 波动方程和能量的关系，在波动方程 $\frac{{\partial }^{2}u}{\partial t^2}-a^2\frac{{\partial }^{2}u}{\partial x^2}=f$ 两端同乘以 $\frac{\partial u}{\partial t}$ 并在区域 $K_{\tau }$ 上积分并按照前面的常用替换得：$${\iint }_{K_{\tau }}{u}_t{u}_{tt}-a^2{u}_t{u}_{xx}dxdt={\iint }_{K_{\tau }}{u}_{t}fdxdt$$$${\iint }_{K_{\tau }}\frac{1}{2}(u_t^2+a^2{u}_x^2{)}_t-a^2(u_t{u}_x{)}_{x}dxdt={\iint }_{K_{\tau }}{u}_{t}fdxdt$$

2. 应用下面这个 $\text{Green}$ 公式将等式左边也就是时空域上的积分转换为边界上的积分
   ∬ Ω ∂ P ∂ t + ∂ Q ∂ x d σ = ∮ ∂ Ω − P d x + Q d t \iint_{\Omega}\frac{\partial P}{\partial t}+\frac{\partial Q}{\parti